语音信号特征研究
语音信号的产生：语音由震动产生，语音的区分通过 频率 区分
1.数据准备：数据采样，根据奈奎斯特采样定律：f-sample=2f-wav，可以捕捉到音频所有的细节
2.预加重（Pre-Emphasis）:语音信号往往会有频谱倾斜现象(Spectral Tit 低频部分比高频多)，需要使用滤波器平衡高频与低频部分的幅度：（原理：高频部分差分值比低频部分更大，此消彼长）
\[y(t) = x(t) - \alpha x(t-1), \ \ \ \ 0.95 < \alpha < 0.99
\]
由于傅里叶变换要求输入的信号是平稳的（算法内部基于连续可导的积分实现），因此出现分帧、加窗
3.分帧（Framing）:口型变化 => 音素变化 =>宏观上看不平稳的，需要采取更微观的标准 => 分帧（帧的长度不小于一个音素的长度，音素持续时间大约为50200ms，因此帧长一般取2050ms）
4.加窗：会让每帧信号两端渐变到0，可以使得频谱上各个峰更细，不容易糊在一起（术语叫做 减轻频谱泄露），但坏处是两端的信号被削弱了，弥补措施是，分帧时相邻帧重叠一部分，两帧之间的时间差叫做帧移（一般10ms），以汉明（Hamming）窗为例（这里的\(0<=n<=N-1\)，\(N\)是窗的宽度）
\[w(n) = 0.54 - 0.46 cos(\frac{2\pi n}{N-1})
\]
5.FFT(快速傅里叶变换)，普通的傅里叶变换是积分形式（即连续函数），计算机无法进行积分这种无线分割累计计算，因此使用足够多的离散断点模拟积分计算 。 以下为计算式子（N通常256/512，方便归一化）
\[P = \frac{|FFT(x_i)|^2}{N}
\]
5.FBank特征（Filter Banks）：得到上面的频率谱后，应用Mel滤波器组，提取Fbank特征（模拟人耳接收声音特征，人耳接收声音时呈非线性，对高频不敏感，要求得到的FBank特征在低频分辨度高、高频分辨度低）
\[m = 2595 log_{10} (1 + \frac{f}{700})
\]
\[f = 700(10^{m/2595} - 1)
\]
\[H_m(k) =
\begin{cases}
\hfill 0 \hfill & k < f(m - 1) \\
\\
\hfill \dfrac{k - f(m - 1)}{f(m) - f(m - 1)} \hfill & f(m - 1) \leq k < f(m) \\
\\
\hfill 1 \hfill & k = f(m) \\
\\
\hfill \dfrac{f(m + 1) - k}{f(m + 1) - f(m)} \hfill & f(m) < k \leq f(m + 1) \\
\\
\hfill 0 \hfill & k > f(m + 1) \\
\end{cases}
\]
由前一步FFT得到的频谱 点乘 Mel三角滤波矩阵
\[Y_t(m) = \sum_{k=1}^{N} H_m(k)|X_t(k)|^2
\]
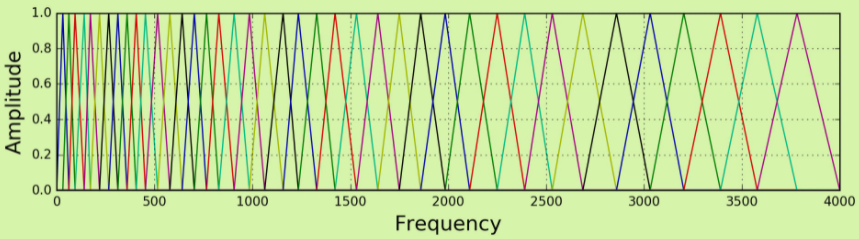如上图所示由多个三角组成，每个三角会对一段区域的频率进行滤波
- MFCC特征(Mel-frequency Cepstral Coefficients)：可以看作压缩特征或者筛选低能量特征，通过DCT（逆傅里叶离散变换的特殊形式）变换进行降维
原理简介：经过傅里叶变换出现低频能量聚集，通过推导实偶信号可以将虚部消除 => 但是信号大多不是偶函数，如下图通过在数轴左侧对称复制平移，即可构造一个 实偶信号 函数 => DCT之后维度并未变换，由于低频能量聚集，可以将高频部分筛除
参考：https://zhuanlan.zhihu.com/p/85299446
