图像分类

二、图像分类

1.K邻近分类法（KNN）

1.KNN算法介绍
邻近算法，也称K最近邻(kNN，k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。 
KNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时，只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

2.KNN算法流程
①计算测试数据与各个训练数据之间的距离； 
②按照距离的递增关系进行排序； 
③选取距离最小的K个点； 
④确定前K个点所在类别的出现频率； 
⑤返回前K个点中出现频率最高的类别作为测试数据的预测分类。

举例：如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。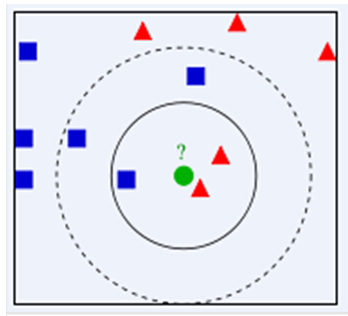

 

 由此也说明了KNN算法的结果很大程度取决于K的选择。

3.KNN算法涉及3个主要因素：

①训练集

②距离或相似的衡量

③K的大小

2.实验及结果

源代码：

1.创建两个不同的二维点集，一个用来训练，一个用来测试。

# -*- coding: utf-8 -*-
from numpy.random import randn
import pickle
from pylab import *

# create sample data of 2D points
n = 200
# two normal distributions
class_1 = 0.6 * randn(n, 2)
class_2 = 1.2 * randn(n, 2) + array([5, 1])
labels = hstack((ones(n), -ones(n)))
# save with Pickle
# with open('points_normal.pkl', 'w') as f:
with open('points_normal_t.pkl', 'wb') as f:
    pickle.dump(class_1, f)
    pickle.dump(class_2, f)
    pickle.dump(labels, f)
# normal distribution and ring around it
print ("save OK!")
class_1 = 0.6 * randn(n, 2)
r = 0.8 * randn(n, 1) + 5
angle = 2 * pi * randn(n, 1)
class_2 = hstack((r * cos(angle), r * sin(angle)))
labels = hstack((ones(n), -ones(n)))
# save with Pickle
# with open('points_ring.pkl', 'w') as f:
with open('points_ring_pkl', 'wb') as f:
    pickle.dump(class_1, f)
    pickle.dump(class_2, f)
    pickle.dump(labels, f)

print ("save OK!")

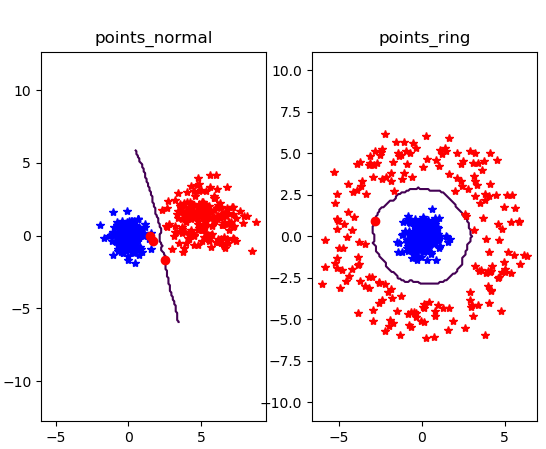
 运行结果：

 

 注意：修改文件名运行两次噢

2.使用KNN分类器对数据进行分类

# -*- coding: utf-8 -*-
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

pklist=['points_normal.pkl','points_ring.pkl']

figure()

# load 2D points using Pickle
for i, pklfile in enumerate(pklist):
    with open('points_normal_t.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)
    # load test data using Pickle
    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
    # test on the first point
    print (model.classify(class_1[0]))

    #define function for plotting
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # lot the classification boundary
    subplot(1,2,i+1)
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
    savefig("test1.png")
show()

 运行结果：

①当k = 3

 

②当k=10

 

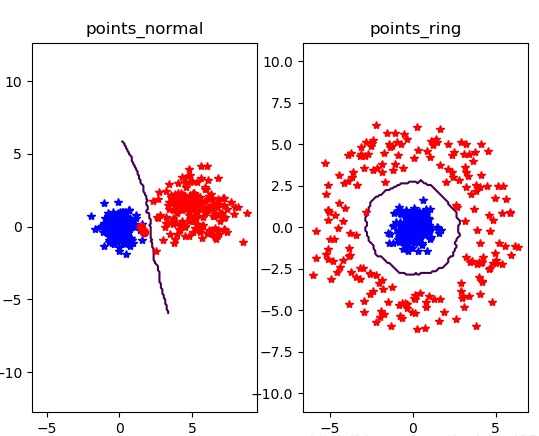
③当k=20