相机标定

一、相机标定原理

一句话就是世界坐标到像素坐标的映射，当然这个世界坐标是我们人为去定义的，标定就是已知标定控制点的世界坐标和像素坐标我们去解算这个映射关系，一旦这个关系解算出来了我们就可以由点的像素坐标去反推它的世界坐标，当然有了这个世界坐标，我们就可以进行测量等其他后续操作了，上述标定又被称作隐参数标定，因为它没有单独求出相机的内部参数，如相机焦虑，相机畸变系数等。在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。

二、张氏相机标定法

1.原理

张正友教授在1998年提出单平面棋盘格的摄像机标定方法。本文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。同时也相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。

在视觉测量中，需要进行的一个重要预备工作是定义四个坐标系的意义，即摄像机坐标系、图像物理坐标系、像素坐标系和世界坐标系（参考坐标系）。

世界坐标系(world coordinate system)：用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入。单位为m。

相机坐标系(camera coordinate system)：在相机上建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。

图像坐标系(image coordinate system)：为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标。单位为m。

像素坐标系 uov是一个二维直角坐标系，反映了相机CCD/CMOS芯片中像素的排列情况。原点o位于图像的左上角，u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素（整数）。

从世界坐标系到相机坐标系：

三维点到三维点的转换，包括R,t（相机外参）等参数

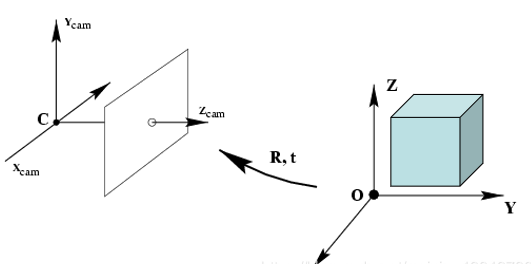
相机坐标系转换为图像坐标系：

三维点到二维点的转换，包括K（相机内参）等参数

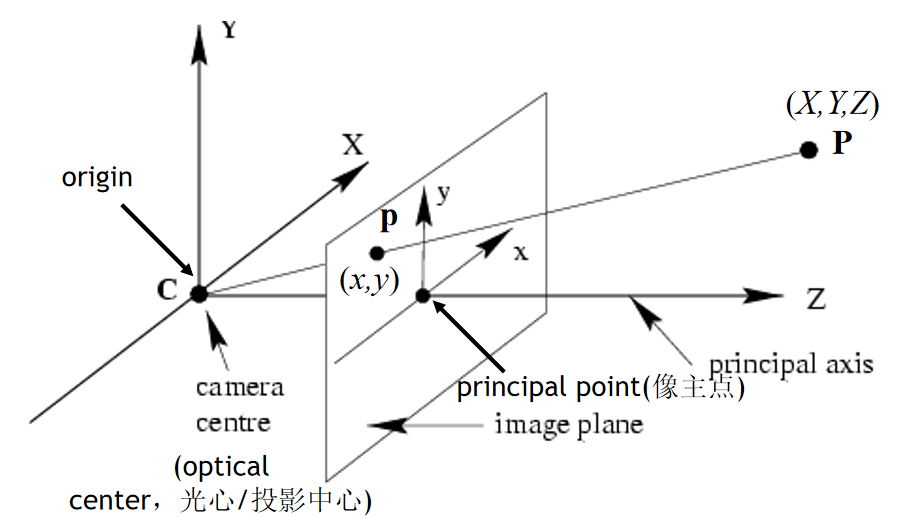
根据上述的关系图可以推导出下面的变换公式：

2.标定平面到图像平面的单应性

由原理可知求解公式为：

其中m的齐次坐标表示图像平面的像素坐标(u,v,1)，M的齐次坐标表示世界坐标系的坐标点(X,Y,Z,1)。R表示旋转矩阵、t表示平移矩阵、S表示尺度因子。A表示摄像机的内参数,具体表达式如下：

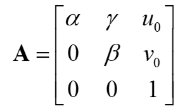
其中α=f/dx，β=f/dy,因为像素不是规规矩矩的正方形，γ代表像素点在x,y方向上尺度的偏差，称为径向畸变参数。s是个尺度因子，对于齐次坐标，尺度因子不会改变坐标值的。我们假设棋盘格位于Z=0。则有以下推理：

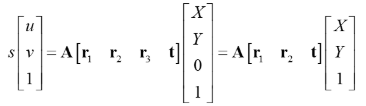
那么我们可以给A[r1 r2 t]一个名字：单应性矩阵。并记H= A[r1 r2 t]。H是一个三3*3的矩阵，并且有一个元素是作为齐次坐标。因此，H有8个未知量待解，所以我们至少需要八个方程。所以需要四个对应点即可算出图像平面到世界平面的单应性矩阵H。

解释：

畸变参数：在几何光学和阴极射线管显示中，畸变是对直线投影的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变。畸变一般可以分为两大类，包括径向畸变和切向畸变。主要的一般径向畸变有时也会有轻微的切向畸变。

三、实验

1.数据集

我准备的是格子数为7×5，内角点为6×4的棋盘格不同角度拍摄的图片，手机型号为华为nova4。

2.流程

①准备来相机标定的图片集；

②对每张图片提取角点信息；

③由于角点信息不够精确，进一步提取亚像素角点信息；

④在图片中画出提取出的角点；

⑤相机标定；

⑥对标定结果评价，计算误差；

⑦使用标定结果对原图片进行矫正；

3.源代码

复制代码

# -*- coding: utf-8 -*-
import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((4 * 6, 3), np.float32)
objp[:, :2] = np.mgrid[0:6, 0:4].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("C:/Users/LE/PycharmProjects/untitled/qi/*.jpg")
i=0;
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (6, 4), None)
    #print(corners)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (6, 4), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        i+=1;
        cv2.imwrite('conimg'+str(i)+'.jpg', img)
        cv2.waitKey(1500)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
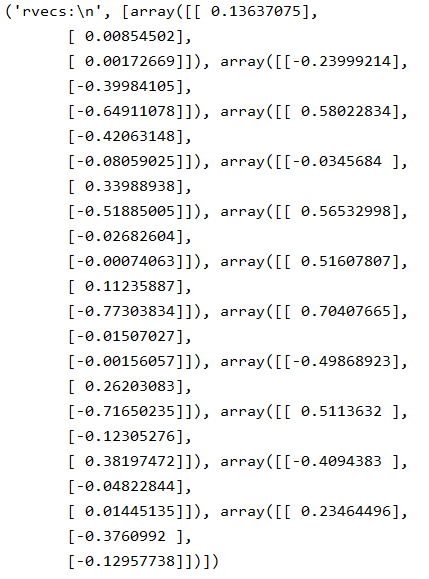
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")

img = cv2.imread(images[2])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片（正常重映射之后会删掉一部分图像）
print (newcameramtx)
print("------------------使用undistort函数-------------------")
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibresult3.jpg', dst1)
#方法一:dst的大小为
print(dst1.shape)