RSA非对称加密(小白也能看懂)
今天和大家聊聊RSA加密算法
首先给大家说一下RSA的历史
RSA加密算法是一种非对称加密算法,在公开密钥加密和电子商业中被广泛使用。RSA是由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)在1977年一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。[1]
1973年,在英国政府通讯总部工作的数学家克利福德·柯克斯(Clifford Cocks)在一个内部文件中提出了一个与之等效的算法,但该算法被列入机密,直到1997年才得到公开。[2]
对极大整数做因数分解的难度决定了 RSA 算法的可靠性。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的 RSA 钥匙才可能被强力方式破解。到目前为止,世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长,用RSA加密的信息实际上是不能被破解的。
1983年9月12日麻省理工学院在美国为RSA算法申请了专利。[3]这个专利于2000年9月21日失效。[4]由于该算法在申请专利前就已经被发表了[5],在世界上大多数其它地区这个专利权不被承认。
然后简单介绍一下RSA的加密原理
天才第一步,雀氏纸尿裤!不是~
-
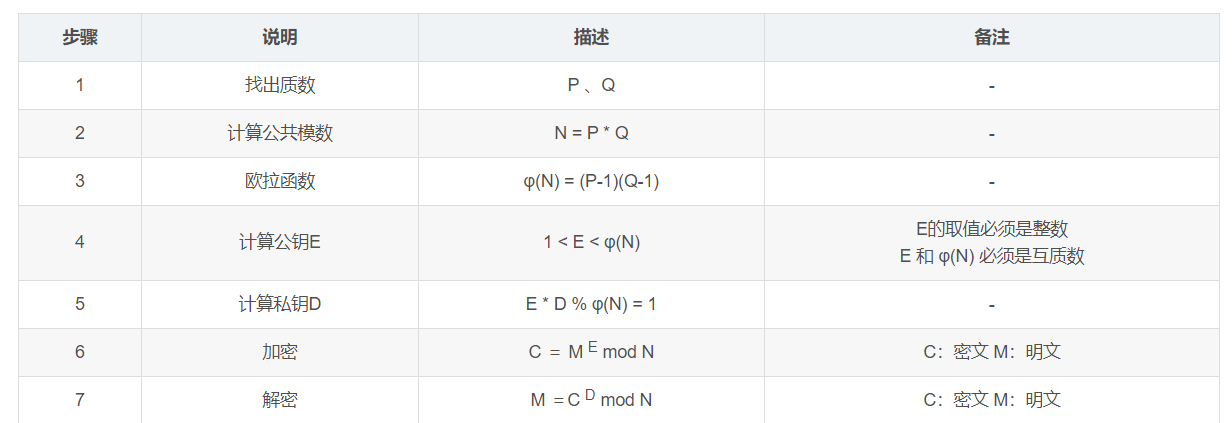
step1:在整数中找到两个素数p与q,要求p与q互质(打死都不能说的)
-
step2:计算N,欧拉函数φ(N)
- N = p*q
-
φ(N)= (p-1)*(q-1)
-
step3:计算公钥e
- 要求:在1到φ(N)之间找到一个e与φ(N)互素
-
step4:计算私钥d
- e*d = 1 (mod φ(N))
-
step5(加密时):进行加密
- c = m^e(mod N)
-
step6(解密时):进行解密
- m = c^d(mod N)
Bingo!

