JOISC 乱写

1|0「JOISC 2020 Day4」首都城市

进行点分治，考虑最终的连通块是否经过当前分治中心，若经过，则当前分治中心的颜色必选，否则分治递归处理。

若一个颜色必选，当前连通块中所有为该颜色的点都要选，一个点被选同时也意味着其到当前分治中心路径上的点也都要选，不断迭代得到当前分治中心的答案即可。

还有另一种做法：若颜色 $i$ 形成的虚树上有颜色为 $j$ 的点，则 $i$ 向 $j$ 连边，意思为选了 $i$ 则必选 $j$。对所有缩点后出度为 $0$ 的点取 $siz-1$ 的最小值即为答案。可以用树剖线段树来优化建图。

2|0「JOISC 2019 Day2」两个天线

只用考虑 $i<j,h_i>h_j$ 的情况，另一种情况取反后再做一遍即可。考虑扫描线，每个位置 $i$ 维护其对应的 $h_i-h_j$ 的最大值。

$i$ 往后起作用的区间为 $[i+a_i,i+b_i]$，将其在相应的位置加入删除即可，加入就是将维护的第一项赋值为 $h_i$，删除就是将其赋值为 $-\infty$。

$j$ 往前起作用的区间为 $[j-b_j,j-a_j]$，将这段区间的第二项和 $-h_j$ 取 $\max$ 即可。

这些操作都可以在线段树上来实现，就是单点修改和区间打标记。

3|0「JOISC 2019 Day2」两道料理

考虑暴力 $DP$，设 $f_{i,j}$ 为第一种到第 $i$ 步，第二种到第 $j$ 步的最大权值，复杂度为 $O(nm)$，无法接受，考虑优化。

将 $DP$ 放到网格图上来考虑，从 $(0,0)$ 走到 $(n,m)$，转移时权值的贡献可以转化为网格图的点是否在路径下方或路径上，如果在，则加上对应的权值。

进一步观察 $DP$ 的过程，发现其从上一列转移过来时，就是先对一些后缀加上一个权值，然后往前不断取 $\max$ 转移过来。考虑对行差分，后缀加变成单点加，然后若一个位置为负数，则将其后面第一个非零位置加上这个数，然后将该位置清零，这样就实现了取 $\max$ 的过程。

用 $set$ 维护非零位置，线段树维护差分即可。

4|0「JOISC 2020 Day3」星座 3

考虑从下往上扫描，对每个纵坐标维护出和该位置冲突且已经选了的星星的权值和。新加入一个星星时，比较删除该星星和删除和其冲突的星星权值，删去权值更小的情况然后更新对应位置的权值即可。

用树状数组维护权值，实现区间加和单点查。发现向上扫描时还需知道每个纵坐标往左往右拓展最远的位置，用两个并查集维护即可。

还有一个笛卡尔树的做法，建出笛卡尔树后，星星等价于笛卡尔树上的一条链，于是问题就转化为了在树上选出若干条不相交的链，使得权值和最大。$DP$ 方式和 [NOI2020] 命运 类似，同样也是线段树合并实现整体 $DP$。

5|0「JOISC 2019 Day3」穿越时空 Bitaro

先将第 $i$ 个城市的时间减去 $i$，这样走向下一个城市就不会流逝时间了，移动就是水平的了：

考虑用一些二元组 $(l,r)$ 和三元组 $(a,b,v)$，来描述经过一段城市的情况。

二元组 $(l,r)$ 表示进入这段城市的时刻在区间 $[l,r]$ 内时，通过这段城市不产生费用，二元组的合并就是取交，当不存在交集时就会产生三元组。

三元组 $(a,b,v)$ 表示进入这段城市的时刻至多为 $a$，出去的时刻至少为 $b$，费用为 $v$。二元组、三元组的合并是满足结合律的，因此可以用线段树来维护。

还有另一种维护分段函数的做法。对于一个城市，可以经过其的时刻为一个区间，因此出去时刻和费用都是关于进入时刻的一次函数，归纳发现对于一段城市，出去时刻和费用是关于进入时刻的三段分段函数。用线段树来维护这个分段函数即可。

6|0「JOISC 2019 Day4」蛋糕拼接 3

发现只要按 $c$ 从小到大排序就能使 $\sum\limits_{j=1}^m|c_{k_j}-c_{k_{j+1}}|$ 达到最小值 $2(c_{\max}-c_{\min})$。

将蛋糕按 $c$ 从小到大排序后，问题就转化为了选出一个贡献最大的区间 $[l,r]$，区间 $[l,r]$ 的贡献为该区间最大的 $m$ 个 $v$ 的和减去 $2(c_r-c_l)$。

类似于 [IOI2014] holiday 假期，本题也是具有决策单调性的，对于每个 $l$，最优的 $r$ 是单调不降的。感性理解为什么有决策单调性就是因为新加入一个 $r$ 后，对于 $l_1<l_2$，$l_2$ 获得的贡献是大于等于 $l_1$ 的。

用分治求解最优决策点，主席树求区间前 $m$ 大的和即可。

7|0「JOISC 2020 Day2」有趣的 Joitter 交友

将二元环缩为一个点集，发现点集都为团，且一个点向点集内任意一点连边后，该点会向这个点集内所有点都连边。并查集维护每个点所在的点集，$set$ 维护每个点集内的点，出边指向的点集，入边所在的点集，入边的起点，像 [WC2021] 括号路径 一样启发式合并点集即可。

8|0「JOISC 2020 Day4」治疗计划

不用按时间顺序来考虑区间，可以直接考虑区间间的两两合并，用 $DP$ 来表示就是设 $f_i$ 为 $t_i$ 时刻 $[1,r_i]$ 都已经被治愈的最小费用，$i$ 能转移到 $j$ 当且仅当 $r_i-l_j+1\geqslant |t_i-t_j|$。

发现转移类似最短路，直接线段树优化建图跑最短路复杂度是 $O(m\log^2 m)$ 的。

实际上有更优的做法：和 [NOI2019] 弹跳 一样，可以不把边建出来，先把绝对值去掉，得 $r_i+1-t_i\geqslant l_j-t_j$ 和 $r_i+1-t_i\geqslant l_j+t_j$，用两棵线段树维护 $l_i-t$ 和 $l_i+t_i$ 最小值。最短路过程中取出一个点 $x$ 后，去两棵线段树上暴力找 $x$ 能转移到的点，转移后把这些点的位置的权值设为 $\infty$ 即可。因为费用为点权，所以每个点只会被松弛一次，得复杂度为 $O(m\log m)$。

9|0「JOISC 2018 Day 3」比太郎的聚会

注意到 $\sum y_i$ 和 $n$ 同阶，考虑根号分治。当 $y_i\geqslant \sqrt n$ 时，这样的询问最多有 $\sqrt n$ 个，暴力拓扑排序求最长路即可。当 $y_i< \sqrt n$ 时，预处理每个点到达的最远的 $\sqrt n$ 个点，因为删去的点 $y_i< \sqrt n$，所以答案一定在预处理的点中产生，直接扫一遍预处理的点即可。

10|0「JOISC 2019 Day3」指定城市

$E_j=1$ 的情况可以通过换根 $DP$ 求出，$E_j=2$ 的情况选的两个点一定是两个叶子节点，在 $lca$ 处统计贡献即可。可以证明，对于 $E_j>2$ 时，一定存在一种情况使得 $E_j-1$ 的最优选择点是 $E_j$ 的最优选择点的子集，也就是每次新增一个点。线段树维护 $dfs$ 序，每次加入收益最大的点，并把其贡献删除即可。

11|0「JOISC 2020 Day1」扫除

先不考虑插入操作，向右扫和向上扫相当于对一个区间内的点横坐标或纵坐标取 $\max$。若两种操作都存在时，一种操作会影响另一种操作的有效范围，如先向上扫后，向右扫能影响到的点的横坐标的区间会缩小：

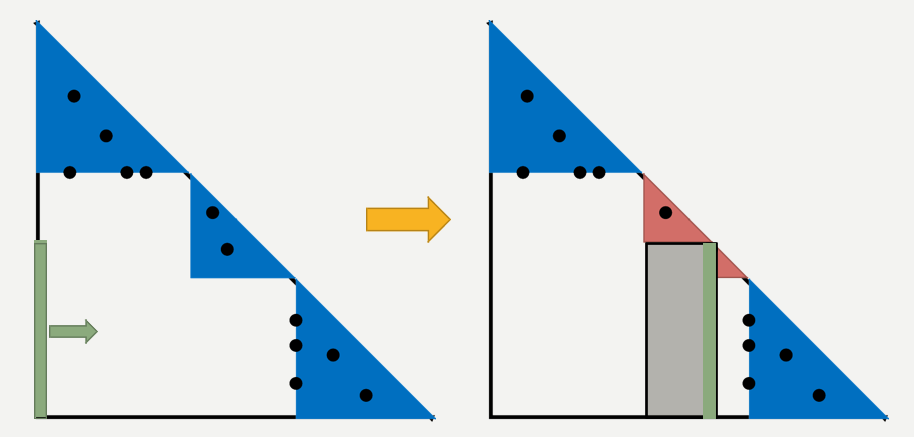
影响另一种操作的有效范围也是一个区间取 $\max$ 的操作，先按时间顺序处理出每个操作的有效范围，然后对横纵坐标分开维护即可。

再考虑上插入操作，一个点可能中途加入，这样就打破了原先点集阶梯状的分布了，但一个点从插入到查询受到的操作是一个连续的区间，用线段树分治来维护即可。用线段树就能实现区间取 $\max$，单点查询。

12|0「JOISC 2019 Day4」合并

一条边两侧的子树出现同种颜色后，这条边就是合法的。将每种颜色的点形成的最小连通块缩成一个点，这里可以用并查集来实现。然后整棵树就都是由不同颜色的点构成的了，答案即为这棵树的最小链覆盖（用最少的链覆盖所有边），设叶子数为 $cnt$，最小链覆盖为 $\left\lceil \frac{cnt}{2} \right\rceil$。

13|0「JOISC 2017 Day 1」港口设施

考虑两个物品，进出栈时间分别为 $l_1,r_1$ 和 $l_2,r_2$，若有 $l_1<l_2<r_1<r_2$，则这两个物品一定在不同栈中。将形如这样的物品间连一条边，若形成的图是二分图则有合法方案，设连通块个数为 $cnt$，答案即为 $2^{cnt}$。直接连边复杂度无法接受，发现一段区间都被连过边后，之后往这个区间的连边只需连一条边来保证连通性，用并查集即可维护。

14|0「JOISC 2017 Day 3」长途巴士

先对乘客按 $D_i$ 排序，服务站按 $S_i\bmod T$ 排序。

考虑对乘客进行 $DP$，设 $f_i$ 表示考虑了前 $i$ 名乘客的最小花费，得转移为：

$$\large f_i=\min \begin{cases} f_{i-1}+\left(\frac{X-D_i}{T}+1\right)W\\ f_j+(i-j)\left( \min\limits_{S_k\bmod T\in[D_i,D_{i+1})} \left\lfloor \frac{S_k}{T} \right\rfloor\right)W+\sum\limits_{k=j+1}^iC_k& j<i \end{cases}$$

第一个转移就是保留乘客 $i$ 到终点，第二个转移是通过少买水，在第 $k$ 个服务站将 $[j+1,i]$ 的乘客下车。

发现转移是斜率优化的形式，但斜率不单调，用栈维护凸包后二分即可。

__EOF__

本文作者：lhm_
本文链接：https://www.cnblogs.com/lhm-/p/14546352.html
关于博主：sjzez 的一名 OI 学生
版权声明：转载标明出处
声援博主：希望得到宝贵的建议