博弈论

定义

公平组合游戏：

1. 完全信息，所有游戏者都能看到整个局势。
2. 无随机行动。所有行动都确定性地将目前局势转变到下一个局势。
3. 在有限步行动之后按照规则游戏必将终止，此时有唯一的一方成为赢家。

必胜状态：双方都采取最优决策下，位于当前状态的必胜。

必败状态：双方都采取最优决策下，位于当前状态的必败。

可以将游戏转化为有向无环图，状态是点，决策是边。

所有终止状态都是必败状态。

一个状态是必胜状态当且仅当存在至少一个必败状态是它的后继状态。

一个状态是必败状态当且仅当它的所有后继状态都是必胜状态。

巴什博奕

\(n\) 个石子，每次至少拿 \(1\) 个，至多拿 \(m\) 个。

当 \((m+1) \mid n\) 则先手必败。

当 \((m+1) \mid n\) 时，当先手拿 \(x\) 个时，后手拿 \(m+1-x\) 个，最后剩下的石头个数一定为 \(m+1\)。当 \((m+1) \not \mid n\) 时，先手可以将石头个数转化为 \((m+1) \mid n\) 的情况。

威佐夫博弈

两堆石子，每次可从某一堆中拿任意个石子，至少拿一个，也可以从两堆中拿相同个数的石子。

设两堆石子个数为 \(a,b\left( a>b \right)\)，当满足 \(\left\lfloor \frac{\sqrt5+1}{2}(a-b) \right\rfloor=b\) 时，先手必败。

斐波那契博弈

\(n\) 个石子，第一次拿石子时可以拿任意个，但不能拿完，至少拿一个，之后每次至少拿 \(1\) 个，至多拿上一次对手拿的个数的两倍。

当 \(n\) 为斐波那契数时，先手必败。

SG 函数

可以将公平组合游戏转化为有向图游戏，然后用 \(\text{SG}\) 函数来解决。

对于集合 \(S\)，定义 \(\text{mex}\) 为：

\[\large \text{mex}(S)=\min \{ x \}\left( x \not \in S,x \in N \right) \]

设 \(next_x\) 为状态 \(x\) 的后继状态集合，定义 \(\text{SG}\) 函数：

\[\large \text{SG}(x)=\text{mex}\{ \text{SG}(y) \}\left( y\in next_x \right) \]

必败状态的 \(\text{SG}\) 函数为 \(0\)，一个游戏的 \(\text{SG}\) 值为起始状态的 \(\text{SG}\) 函数值。

当一个组合游戏由多个有向图游戏组成，其 \(\text{SG}\) 值为每个游戏的 \(\text{SG}\) 值的异或和，当且仅当该游戏 \(\text{SG}\) 值非 \(0\)，该游戏先手必胜，该定理被称为 \(\text{SG}\) 定理。

Nim 游戏

\(n\) 堆石子，每次可从某一堆中拿任意个石子，至少拿一个。

异或和为 \(0\) 时先手必败。用 \(\text{SG}\) 函数易证。

阶梯 Nim 游戏

\(n\) 个位置，编号 \(1\) 到 \(n\)，每个位置上为一堆石子，每次可从一个位置 \(i\) 拿任意个石子移动到 \(i-1\) 位置，至少拿一个。终止状态为所有石子到位置 \(0\)。

奇数位置异或和为 \(0\) 时先手必败。

只能操作奇数位置时，其就是 \(Nim\) 游戏。若有人操作偶数位置，后手可以将奇数位置增加的石子再拿到下一个偶数位置，对 \(Nim\) 游戏的结果没有影响。

Anti-SG 游戏

所有终止状态都是必胜状态。

规定当所有单一游戏的 \(\text{SG}\) 值为 \(0\) 时，游戏结束。

游戏 \(\text{SG}\) 值非 \(0\) 时，且存在一个单一游戏的 \(\text{SG}\) 值大于 \(1\)。

游戏 \(\text{SG}\) 值为 \(0\) 时，且不存在一个单一游戏的 \(\text{SG}\) 值大于 \(1\)。

满足这两个条件中的一个时，先手必胜，该定理被称为 \(SJ\) 定理。

Multi-SG 游戏

符合拓扑序下，一个单一游戏的后继可以为多个单一游戏。

用 \(Nim\) 游戏来举例，就是加入可以将一堆石子分裂为多堆的决策。

该单一游戏的后继的 \(\text{SG}\) 值为这多个单一游戏的 \(\text{SG}\) 值的异或和。

Every-SG 游戏

每次决策必须操作一遍所有的未到达终止状态的单一游戏。

考虑到整个游戏的胜败只与最后结束的游戏有关，因此最优决策是让自己能取得必胜的游戏尽可能晚的结束。

所以 \(Every-SG\) 游戏还需考虑游戏结束的长短，设函数 \(step(x)\) 表示状态 \(x\) 到达终止状态的最长步数，得：

\[\large step(x) = \begin{cases} \max\{ step(y) \}+1 &y\in next_x,\text{SG}(x)>0,\text{SG}(y)=0 \\ \\ \min\{ step(y) \}+1 &y\in next_x,\text{SG}(x)=0 \\ \end{cases}\\ \]

若状态 \(x\) 为终止状态，则 \(step(x)=0\)。

对于每个单一游戏，必胜状态的 \(step\) 值为奇数，必败状态的 \(step\) 值为奇数。

\(Every-SG\) 游戏先手必胜当且仅当单一游戏中最大的 \(step\) 值为奇数。

翻硬币游戏

\(n\) 枚硬币，有的正面朝上，有的反面朝上，在某些约束下可以翻一些硬币，但是翻的这些硬币中最右边的必须是从正面翻到反面。

一个状态的 \(\text{SG}\) 值为当前状态的每个正面朝上的硬币单一存在时的 \(\text{SG}\) 值的异或和。

考虑证明每个硬币是独立的：翻硬币游戏等价于异或游戏，考虑加游戏，加游戏是每个位置独立的，考虑 \(\text{SG}\) 函数，相同的加游戏可以消去，也就是每位 \(\text{mod}\ 2\)，因此其和异或游戏等价于加游戏，所以每个硬币独立。

树的删边游戏

给定一棵 \(n\) 个点的有根树，每次删去一条边，不与根节点连通的部分删去。

叶子节点 \(\text{SG}\) 值为 \(0\)，其他节点的 \(\text{SG}\) 值为其所有儿子的 \(\text{SG}\) 值加 \(1\) 后的异或和。

加 \(1\) 是因为儿子还有父边，归纳证明即可。

无向图的删边游戏

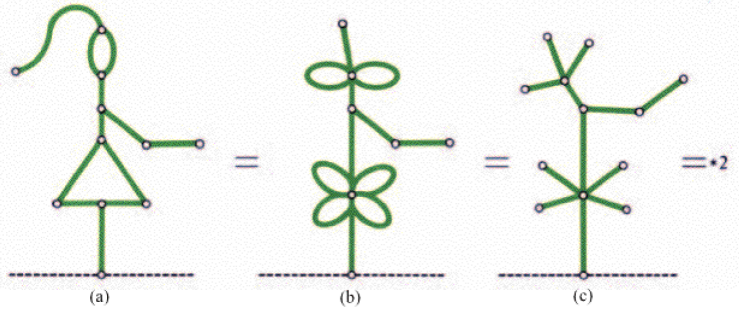
任意一个偶环缩成一个新点，任意一个奇环缩成一个新点加一个新边，原先和环相连的边连到新点上，图的 \(\text{SG}\) 值不会改变，该定理被称为 \(Fusion\ Principle\)。

奇数条边的点双直接当作奇环处理，偶数条边的点双直接当作偶环处理，也就是直接建圆方树，奇数条边点双加一条新边即可。

这样就将无向图的删边游戏转化为了树的删边游戏。