Splay
二叉查找树,对于任意一个节点,该节点的关键码大于它的左子树中任意节点的关键码,该节点的关键码小于它的右子树中任意节点的关键码,且没有键值相等的点
二叉查找树的中序遍历是一个关键码单调递增的节点序列
数组及变量
\(fa[i]:\) 节点\(i\)的父节点
\(son[i][0]:\) 节点\(i\)的左儿子
\(son[i][1]:\) 节点\(i\)的右儿子
\(val[i]:\) 节点\(i\)的关键字
\(siz[i]:\) 以节点\(i\)为根的子树元素个数
\(cnt[i]:\) 节点\(i\)所表示的元素的出现次数
\(tot:\) 共有多少元素
\(root:\) 树的根
函数
\(check:\) 判断节点\(x\)是它父亲的左儿子还是右儿子
\(pushup:\) 更新节点\(x\)的\(siz\)
\(rotate:\) 将是左儿子的右旋,是右儿子的左旋
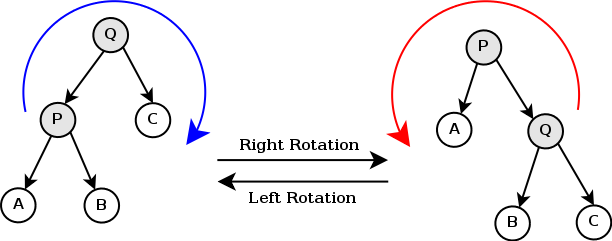
\(splay :\) 进行伸展,不断\(rotate\)直到达到目标状态
\(insert:\) 插入一个值
\(find:\) 查找\(x\)的位置,并将其旋转到根节点
\(query\_rnk:\) 查询\(x\)的排名
\(query\_val:\) 查询排名为\(x\)的数
\(get:\) \(k=0\)时,求\(x\)的前驱,\(k=1\)时,求\(x\)的后继
\(del:\) 删除为\(x\)的数
\(code\):
bool check(int x)
{
return ch[fa[x]][1]==x;
}
void pushup(int x)
{
siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+cnt[x];
}
void rotate(int x)
{
int y=fa[x],z=fa[y],k=check(x),w=ch[x][k^1];
ch[z][check(y)]=x,ch[x][k^1]=y,ch[y][k]=w;
fa[w]=y,fa[x]=z,fa[y]=x;
pushup(y),pushup(x);
}
void splay(int x,int goal)
{
for(int y;fa[x]!=goal;rotate(x))
if(fa[y=fa[x]]!=goal)
rotate(check(x)^check(y)?x:y);
if(!goal) root=x;
}
void insert(int x)
{
int p=root,f=0;
while(p&&val[p]!=x) f=p,p=ch[p][val[p]<x];
if(p) cnt[p]++;
else p=++tot,ch[f][val[f]<x]=p,fa[p]=f,val[p]=x,cnt[p]=1;
splay(p,0);
}
void find(int x)
{
int p=root;
while(ch[p][val[p]<x]&&x!=val[p]) p=ch[p][val[p]<x];
splay(p,0);
}
int query_rnk(int x)
{
find(x);
return siz[ch[root][0]];
}
int query_val(int x)
{
x++;
int p=root;
while(1)
{
if(x<=siz[ch[p][0]]) p=ch[p][0];
else
{
x-=siz[ch[p][0]]+cnt[p];
if(x<=0) return val[p];
p=ch[p][1];
}
}
}
int get(int x,int k)
{
find(x);
if(val[root]>x&&k) return root;
if(val[root]<x&&!k) return root;
int p=ch[root][k];
while(ch[p][k^1]) p=ch[p][k^1];
return p;
}
void del(int x)
{
int pre=get(x,0),nxt=get(x,1);
splay(pre,0),splay(nxt,pre);
int d=ch[nxt][0];
if(cnt[d]>1) cnt[d]--,splay(d,0);
else ch[nxt][0]=0;
}
......
insert(inf),insert(-inf);
insert(a)
del(a)
query_rnk(a)
query_val(a)
key[get(a,0)]
key[get(a,1)]
\(Splay\)进行序列操作,按序列编号为关键字建二叉搜索树,二叉搜索树的中序遍历为原序列
维护一个数列,共 \(7\) 种操作:
I. INSERT x n a1 a2 .. an 在第 \(x\) 个数后插入 \(n\) 个数分别为 \(a_1\dots a_n\)。
II. DELETE x n 删除第 \(x\) 个数开始的 \(n\) 个数。
III. REVERSE x n 翻转第 \(x\) 个数开始的 \(n\) 个数的区间。
IV. MAKE-SAME x n t 将第 \(x\) 个数开始的 \(n\) 个数统一改为 \(t\)。
V. GET-SUM x n 输出第 \(x\) 个数开始的 \(n\) 个数的和。
VI. GET x 输出第 \(x\) 个数的值。
VII. MAX-SUM x n 输出第 \(x\) 个数开始的 \(n\) 个数的最大连续子序列和。
\(code:\)
bool check(int x)
{
return ch[fa[x]][1]==x;
}
void pushup(int x)
{
int ls=ch[x][0],rs=ch[x][1];
siz[x]=siz[ls]+siz[rs]+1;
sum[x]=sum[ls]+sum[rs]+val[x];
lm[x]=max(lm[ls],sum[ls]+val[x]+lm[rs]);
rm[x]=max(rm[rs],sum[rs]+val[x]+rm[ls]);
ma[x]=max(val[x]+lm[rs]+rm[ls],max(ma[ls],ma[rs]));
}
void pushr(int x)
{
rev[x]^=1,swap(ch[x][0],ch[x][1]),swap(lm[x],rm[x]);
}
void pushv(int x,int v)
{
if(!x) return;
tag[x]=1,val[x]=v,sum[x]=v*siz[x];
lm[x]=rm[x]=max(sum[x],0),ma[x]=max(sum[x],val[x]);
}
void pushdown(int x)
{
int ls=ch[x][0],rs=ch[x][1];
if(tag[x]) pushv(ls,val[x]),pushv(rs,val[x]);
if(rev[x]) pushr(ls),pushr(rs);
tag[x]=rev[x]=0;
}
int add()
{
int x=top?st[top--]:++tot;
fa[x]=ch[x][0]=ch[x][1]=rev[x]=siz[x]=tag[x]=0;
return x;
}
void build(int l,int r,int &x,int *a)
{
x=add();
int mid=(l+r)>>1;
lm[x]=rm[x]=max(a[mid],0);
val[x]=ma[x]=sum[x]=a[mid];
if(l<mid) build(l,mid-1,ch[x][0],a);
if(r>mid) build(mid+1,r,ch[x][1],a);
fa[ch[x][0]]=fa[ch[x][1]]=x;
pushup(x);
}
void rotate(int x)
{
int y=fa[x],z=fa[y],k=check(x),w=ch[x][k^1];
ch[z][check(y)]=x,ch[x][k^1]=y,ch[y][k]=w;
fa[w]=y,fa[x]=z,fa[y]=x;
pushup(y),pushup(x);
}
void splay(int x,int goal)
{
for(int y;fa[x]!=goal;rotate(x))
if(fa[y=fa[x]]!=goal)
rotate(check(x)^check(y)?x:y);
if(!goal) root=x;
}
int kth(int x,int rk)
{
pushdown(x);
int ls=ch[x][0],rs=ch[x][1];
if(rk==siz[ls]+1) return x;
if(rk<=siz[ls]) return kth(ls,rk);
return kth(rs,rk-siz[ls]-1);
}
void split(int l,int r)
{
l=kth(root,l-1),r=kth(root,r+1),splay(l,0),splay(r,l);
}
void insert(int x,int num)
{
int t,p;
build(1,num,t,c);
split(x+1,x);
p=ch[root][1];
ch[p][0]=t,fa[t]=p;
pushup(p),pushup(root);
}
void del(int x)
{
if(!x) return;
st[++top]=x;
del(ch[x][0]),del(ch[x][1]);
}
void erase(int l,int r)
{
int p;
split(l,r);
p=ch[root][1];
del(ch[p][0]),ch[p][0]=0;
pushup(p),pushup(root);
}
void cover(int l,int r,int v)
{
int p;
split(l,r);
p=ch[root][1];
pushv(ch[p][0],v);
pushup(p),pushup(root);
}
void reverse(int l,int r)
{
int p;
split(l,r);
p=ch[root][1];
pushr(ch[p][0]);
pushup(p),pushup(root);
}
int query_sum(int l,int r)
{
int p;
split(l,r);
p=ch[root][1];
return sum[ch[p][0]];
}
int query_max(int l,int r)
{
int p;
split(l,r);
p=ch[root][1];
return ma[ch[p][0]];
}
......
if(opt=="GET") read(x),printf("%d\n",val[kth(root,x+1)]);
else read(x),read(num),x++;
if(opt=="INSERT")
{
for(int i=1;i<=num;++i) read(c[i]);
insert(x,num);
}
if(opt=="DELETE") erase(x,x+num-1);
if(opt=="REVERSE") reverse(x,x+num-1);
if(opt=="MAKE-SAME") read(v),cover(x,x+num-1,v);
if(opt=="GET-SUM") printf("%d\n",query_sum(x,x+num-1));
if(opt=="MAX-SUM") printf("%d\n",query_max(x,x+num-1));


 浙公网安备 33010602011771号
浙公网安备 33010602011771号