JS数据结构

数据结构：计算机存储、组织数据的方式，数据结构意味着接口或封装：一个数据结构可被视为两个函数之间的接口，或者是由数据类型联合组成的存储内容的访问方法封装

常见的数据结构：

1、数组（Array）

数组是最简单的内存数据结构

2、栈（Stack）

栈是一种遵循后进先出（LIFO）原则的有序集合。新添加的或待删除的元素都保存在栈的同一端，称作栈顶，另一端就叫栈底。在栈里，新元素都接近栈顶，旧元素都接近栈底。

栈常用的有以下几个方法：

1、push 添加一个（或几个）新元素到栈顶

2、pop 溢出栈顶元素，同时返回被移除的元素

3、peek 返回栈顶元素，不对栈做修改

4、isEmpty` 栈内无元素返回 `true`，否则返回 `false

5、size 返回栈内元素个数

6、clear 清空栈

class Stack {
 constructor() {
   this.stackList = []; // 储存数据
 }
 // 向栈内压入一个元素
 push(item) {
   this.stackList.push(item);
 }
 // 把栈顶元素弹出
 pop() {
   return this.stackList.pop();
 }
 // 返回栈顶元素
 peek() {
   return this.stackList[this.stackList.length - 1];
 }
 // 判断栈是否为空
 isEmpty() {
   return !this.stackList.length;
 }
 // 栈元素个数
 size() {
   return this.stackList.length;
 }
 // 清空栈
 clear() {
   this.stackList = [];
 }
}

总结：栈仅仅只是对原有数据进行了一次封装而已。而封装的结果是：并不去关心其内部的元素是什么，只是去操作栈顶元素

3、队列（Queue）

队列是遵循先进先出（FIFO，也称为先来先服务）原则的一组有序的项。队列在尾部添加新元素，并从顶部移除元素。最新添加的元素必须排在队列的末尾，向队列的后端位置添加实体，称为入队（enqueue)，并从队列的前端位置移除实体，称为出队(dequeue)

队列常用的有以下几个方法：

1、enqueue 向队列尾部添加一个(或多个)新的项

2、dequeue 移除队列的第一(即排在队列最前面的)项，并返回被移除的元素

3、head 返回队列第一个元素，队列不做任何变动

4、tail 返回队列最后一个元素，队列不做任何变动

5、isEmpty` 队列内无元素返回 `true`，否则返回 `false

6、size 返回队列内元素个数

7、clear 清空队列

class Queue {
 constructor() {
   this.queueList = [];
 }
 // 向队列尾部添加一个(或多个)新的项
 enqueue(item) {
   this.queueList.push(item);
 }
 // 移除队列的第一(即排在队列最前面的)项
 dequeue() {
   return this.queueList.shift();
 }
 // 返回队列第一个元素
 head() {
   return this.queueList[0];
 }
 // 返回队列最后一个元素
 tail() {
   return this.queueList[this.queueList.length - 1];
 }
 // 队列是否为空
 isEmpty() {
   return !this.queueList.length;
 }
 // 返回队列内元素个数
 size() {
   return this.queueList.length;
 }
 // 清空队列
 clear() {
   this.queueList = [];
 }
}

总结：栈仅能操作其头部，队列则首尾均能操作，但仅能在头部出尾部进，栈和队列并不关心其内部元素细节，也无法直接操作非首尾元素

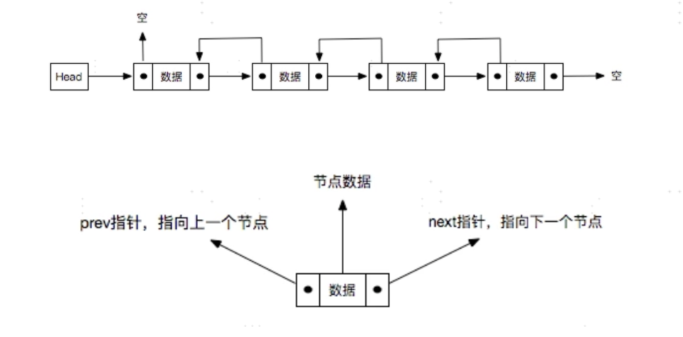
4、链表（Linked List）

链表分为单向链表和双向链表，数组的插入以及删除都有可能会是一个O(n)的操作。从而就引出了链表这种数据结构，链表不要求逻辑上相邻的元素在物理位置上也相邻，因此它没有顺序存储结构所具有的缺点，当然它也失去了数组在一块连续空间内随机存取的优点

单向链表

单向链表的特点：

用一组任意的内存空间去存储数据元素（这里的内存空间可以是连续的，也可以是不连续的）
每个节点(node)都由数据本身和一个指向后续节点的指针组成
整个链表的存取必须从头指针开始，头指针指向第一个节点
最后一个节点的指针指向空（NULL）

// 初始化节点
class ListNode {
  constructor(key) {
    this.next = null;
    this.key = key;
  }
}
// 初始化单向链表
class List {
  constructor() {
    this.head = null;
    this.length = 0;
  }

  static createNode(key) {
    return new ListNode(key);
  }

  // 往头部插入数据
  insert(node) {
    // 如果head后面有指向的节点
    if (this.head) {
      node.next = this.head;
    } else {
      node.next = null;
    }
    this.head = node;
    this.length++;
  }
  // 搜索节点从head开始查找 找到节点中的key等于想要查找的key的时候，返回该节点
  find(key) {
    let node = this.head;
    while (node !== null && node.key !== key) {
      node = node.next;
    }
    return node;
  }

  delete(node) {
    if (this.length === 0) {
      throw 'node is undefined';
    }
    // 所要删除的节点刚好是第一个
    if (node === this.head) {
      this.head = node.next;
      this.length--;
      return;
    }
    let prevNode = this.head;
    while (prevNode.next !== node) {
      prevNode = prevNode.next;
    }
    // 要删除的节点为最后一个节点
    if (node.next === null) {
      prevNode.next = null;
    }
    // 在列表中间删除某个节点
    if (node.next) {
      prevNode.next = node.next;
    }
    this.length--;
  }
}

双向链表

双向链表多了一个指向上一个节点的指针！！！

// 初始化节点
class ListNode {
  constructor(key) {
    // 指向前一个节点
    this.prev = null;
    // 指向后一个节点
    this.next = null;
    // 节点的数据(或者用于查找的键)
    this.key = key;
  }
}

// 双向链表
class List {
  constructor() {
    this.head = null;
  }

  static createNode(key) {
    return new ListNode(key);
  }
  // 插入
  insert(node) {
    node.prev = null;
    node.next = this.head;
    if (this.head) {
      this.head.prev = node;
    }
    this.head = node;
  }
  // 搜索节点
  find(key) {
    let node = this.head;
    while (node !== null && node.key !== key) {
      node = node.next;
    }
    return node;
  }
  // 删除节点
  delete(node) {
    const { prev, next } = node;
    delete node.prev;
    delete node.next;
    // 删除的是第一个节点
    if (node === this.head) {
      this.head = next;
    }
    // 删除的是中间的某个节点
    if (prev) {
      prev.next = next;
    }
    // 删除的是最后一个节点
    if (next) {
      next.prev = prev;
    }
  }
}

总结：链表可以理解为有一个head，然后在有好多的节点(Node)，用一个指针把他们串起来，至于里面的插入操作也好，删除也好，其实都是在调整节点中指针的指向。

5、树（Tree）

树是一种分层数据的抽象模型，一棵树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点

二叉树

二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点

二叉搜索树（BST）是二叉树的一种，但是它只允许你在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大（或者等于）的值

function BinarySearchTree() {
    var Node = function(key){
        this.key = key;
        this.left = null;
        this.right = null;
    };
    var root = null;
    // 向树中插入一个新的键
    this.insert = function(key){
        var newNode = new Node(key);
        // special case - first element
        if (root === null){
            root = newNode;
        } else {
            insertNode(root,newNode);
        }
    };

    var insertNode = function(node, newNode){
        if (newNode.key < node.key){
            if (node.left === null){
                node.left = newNode;
            } else {
                insertNode(node.left, newNode);
            }
        } else {
            if (node.right === null){
                node.right = newNode;
            } else {
                insertNode(node.right, newNode);
            }
        }
    };

    this.getRoot = function(){
        return root;
    };
    
    // 在树中查找一个键，如果节点存在，则返回true；如果不存在，则返回 false
    this.search = function(key){
        return searchNode(root, key);
    };
    var searchNode = function(node, key){
        if (node === null){
            return false;
        }
        if (key < node.key){
            return searchNode(node.left, key);
        } else if (key > node.key){
            return searchNode(node.right, key);
        } else { //element is equal to node.item
            return true;
        }
    };
    // 通过中序遍历方式遍历所有节点
    this.inOrderTraverse = function(callback){
        inOrderTraverseNode(root, callback);
    };
    var inOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            inOrderTraverseNode(node.left, callback);
            callback(node.key);
            inOrderTraverseNode(node.right, callback);
        }
    };
    // 通过先序遍历方式遍历所有节点
    this.preOrderTraverse = function(callback){
        preOrderTraverseNode(root, callback);
    };
    var preOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            callback(node.key);
            preOrderTraverseNode(node.left, callback);
            preOrderTraverseNode(node.right, callback);
        }
    };
    // 通过后序遍历方式遍历所有节点
    this.postOrderTraverse = function(callback){
        postOrderTraverseNode(root, callback);
    };
    var postOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            postOrderTraverseNode(node.left, callback);
            postOrderTraverseNode(node.right, callback);
            callback(node.key);
        }
    };
    // 返回树中最小的值/键
    this.min = function() {
        return minNode(root);
    };
    var minNode = function (node) {
        if (node){
            while (node && node.left !== null) {
                node = node.left;
            }
            return node.key;
        }
        return null;
    };
    // 返回树中最大的值/键
    this.max = function() {
        return maxNode(root);
    };
    var maxNode = function (node) {
        if (node){
            while (node && node.right !== null) {
                node = node.right;
            }
            return node.key;
        }
        return null;
    };
    // 从树中移除某个键
    this.remove = function(element){
        root = removeNode(root, element);
    };
    var findMinNode = function(node){
        while (node && node.left !== null) {
            node = node.left;
        }
        return node;
    };
    var removeNode = function(node, element){
        if (node === null){
            return null;
        }
        if (element < node.key){
            node.left = removeNode(node.left, element);
            return node;
        } else if (element > node.key){
            node.right = removeNode(node.right, element);
            return node;
        } else { 
            // element is equal to node.item
            // handle 3 special conditions
            // 1 - a leaf node
            // 2 - a node with only 1 child
            // 3 - a node with 2 children

            //case 1
            if (node.left === null && node.right === null){
                node = null;
                return node;
            }
            //case 2
            if (node.left === null){
                node = node.right;
                return node;
            } else if (node.right === null){
                node = node.left;
                return node;
            }
            //case 3
            var aux = findMinNode(node.right);
            node.key = aux.key;
            node.right = removeNode(node.right, aux.key);
            return node;
        }
    };
}

AVL树 是一种自平衡二叉搜索树，意思是任何一个节点左右两侧子树的高度之差最多为1。也就是说这种树会在添加或移除节点时尽量试着成为一棵完全树，在AVL树中插入或移除节点和BST完全相同

function AVLTree() {

    var Node = function(key){
        this.key = key;
        this.left = null;
        this.right = null;
    };

    var root = null;

    this.getRoot = function(){
        return root;
    };

    var heightNode = function(node) {
        if (node === null) {
            return -1;
        } else {
            return Math.max(heightNode(node.left), heightNode(node.right)) + 1;
        }
    };
    // 左-左（LL）：向右的单旋转
    var rotationLL = function(node) {
        var tmp = node.left;
        node.left = tmp.right;
        tmp.right = node;

        return tmp;
    };
    // 右-右（RR）：向左的单旋转
    var rotationRR = function(node) {
        var tmp = node.right;
        node.right = tmp.left;
        tmp.left = node;
        return tmp;
    };
    // 左-右（LR）：向右的双旋转
    var rotationLR = function(node) {
        node.left = rotationRR(node.left);
        return rotationLL(node);
    };
    // 右-左（RL）：向左的双旋转 
    var rotationRL = function(node) {
        node.right = rotationLL(node.right);
        return rotationRR(node);
    };

    var insertNode = function(node, element) {
        if (node === null) {
            node = new Node(element);
        } else if (element < node.key) {
            node.left = insertNode(node.left, element);
            if (node.left !== null) {
                if ((heightNode(node.left) - heightNode(node.right)) > 1){
                    if (element < node.left.key){
                        node = rotationLL(node);
                    } else {
                        node = rotationLR(node);
                    }
                }
            }
        } else if (element > node.key) {
            node.right = insertNode(node.right, element);
            if (node.right !== null) {
                if ((heightNode(node.right) - heightNode(node.left)) > 1){
                    if (element > node.right.key){
                        node = rotationRR(node);
                    } else {
                        node = rotationRL(node);
                    }
                }
            }
        }
        return node;
    };

    this.insert = function(element) {
        root = insertNode(root, element);
    };

    var parentNode;
    var nodeToBeDeleted;

    var removeNode = function(node, element) {
        if (node === null) {
            return null;
        }
        parentNode = node;

        if (element < node.key) {
            node.left = removeNode(node.left, element);
        } else {
            nodeToBeDeleted = node;
            node.right = removeNode(node.right, element);
        }

        if (node === parentNode) { //remove node
            if (nodeToBeDeleted !== null && element === nodeToBeDeleted.key) {
                if (nodeToBeDeleted === parentNode) {
                    node = node.left;
                } else {
                    var tmp = nodeToBeDeleted.key;
                    nodeToBeDeleted.key = parentNode.key;
                    parentNode.key = tmp;
                    node = node.right;
                }
            }
        } else { // do balancing
            if (node.left === undefined) node.left = null;
            if (node.right === undefined) node.right = null;

            if ((heightNode(node.left) - heightNode(node.right)) === 2) {
                if (element < node.left.key) {
                    node = rotationLR(node);
                } else {
                    node = rotationLL(node);
                }
            }

            if ((heightNode(node.right) - heightNode(node.left)) === 2) {
                if (element > node.right.key) {
                    node = rotationRL(node);
                } else {
                    node = rotationRR(node);
                }
            }
        }

        return node;
    };

    this.remove = function(element) {
        parentNode = null;
        nodeToBeDeleted = null;
        root = removeNode(root, element);
    };
}

红黑树（Red Black Tree）是一种自平衡二叉查找树，红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能

节点是红色或黑色

根节点是黑色
每个叶子节点都是黑色的空节点(null)
每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

function RedBlackTree() {

    var Colors = {
        RED: 0, // 红色节点
        BLACK: 1 // 黑色节点
    };

    var Node = function (key, color) {
        this.key = key;
        this.left = null;
        this.right = null;
        this.color = color;

        this.flipColor = function(){
            if (this.color === Colors.RED) {
                this.color = Colors.BLACK;
            } else {
                this.color = Colors.RED;
            }
        };
    };

    var root = null;

    this.getRoot = function () {
        return root;
    };

    var isRed = function(node){
        if (!node){
            return false;
        }
        return node.color === Colors.RED;
    };

    var flipColors = function(node){
        node.left.flipColor();
        node.right.flipColor();
    };

    var rotateLeft = function(node){
        var temp = node.right;
        if (temp !== null) {
            node.right = temp.left;
            temp.left = node;
            temp.color = node.color;
            node.color = Colors.RED;
        }
        return temp;
    };

    var rotateRight = function (node) {
        var temp = node.left;
        if (temp !== null) {
            node.left = temp.right;
            temp.right = node;
            temp.color = node.color;
            node.color = Colors.RED;
        }
        return temp;
    };

    var insertNode = function(node, element) {

        if (node === null) {
            return new Node(element, Colors.RED);
        }

        var newRoot = node;

        if (element < node.key) {
            node.left = insertNode(node.left, element);
        } else if (element > node.key) {
            node.right = insertNode(node.right, element);
        } else {
            node.key = element;
        }

        if (isRed(node.right) && !isRed(node.left)) {
            newRoot = rotateLeft(node);
        }

        if (isRed(node.left) && isRed(node.left.left)) {
            newRoot = rotateRight(node);
        }
        if (isRed(node.left) && isRed(node.right)) {
            flipColors(node);
        }
        return newRoot;
    };

    this.insert = function(element) {
        root = insertNode(root, element);
        root.color = Colors.BLACK;
    };
}

6、图（Graph）

图是网络结构的抽象模型。图是一组由边连接的节点（或顶点）

一个图G = (V, E)由以下元素组成

V：一组顶点
E：一组边，连接V中的顶点

图最常见的实现是邻接矩阵、关联矩阵、邻接表，有两种算法可以对图进行遍历：广度优先搜索（Breadth-First Search，BFS）和深度优先搜索（Depth-First Search，DFS）。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环等

算法数据结构描述
深度优先搜索栈通过将顶点存入栈中，顶点是沿着路径被探索的，存在新的相邻顶点就去访问
广度优先搜索队列通过将顶点存入队列中，最先入队列的顶点先被探索

7、堆（Heap）

堆通常是一个可以被看做一棵树的数组对象，堆的实现通过构造二叉堆，实为二叉树的一种

特点

任意节点小于（或大于）它的所有子节点
堆总是一棵完全树。即除了最底层，其他层的节点都被元素填满，且最底层从左到右填入。
将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

基本类型

包含null、undefined、Number、String、Boolean，ES6还多了一种Symbol

基本数据类型可以直接访问，他们是按照值进行分配的，存放在栈(stack)内存中的简单数据段，数据大小确定，内存空间大小可以分配。

引用型

即Object ，是存放在堆(heap)内存中的对象，变量实际保存的是一个指针，这个指针指向另一个位置

堆的每个节点的左边子节点索引是 i * 2 + 1，右边是 i * 2 + 2，父节点是 (i - 1) /2
堆有两个核心的操作，分别是 shiftUp 和 shiftDown 。前者用于添加元素，后者用于删除根节点
shiftUp 的核心思路是一路将节点与父节点对比大小，如果比父节点大，就和父节点交换位置
shiftDown 的核心思路是先将根节点和末尾交换位置，然后移除末尾元素。接下来循环判断父节点和两个子节点的大小，如果子节点大，就把最大的子节点和父节点交换

class MaxHeap {
  constructor() {
    this.heap = []
  }
  size() {
    return this.heap.length
  }
  empty() {
    return this.size() == 0
  }
  add(item) {
    this.heap.push(item)
    this._shiftUp(this.size() - 1)
  }
  removeMax() {
    this._shiftDown(0)
  }
  getParentIndex(k) {
    return parseInt((k - 1) / 2)
  }
  getLeftIndex(k) {
    return k * 2 + 1
  }
  _shiftUp(k) {
    // 如果当前节点比父节点大，就交换
    while (this.heap[k] > this.heap[this.getParentIndex(k)]) {
      this._swap(k, this.getParentIndex(k))
      // 将索引变成父节点
      k = this.getParentIndex(k)
    }
  }
  _shiftDown(k) {
    // 交换首位并删除末尾
    this._swap(k, this.size() - 1)
    this.heap.splice(this.size() - 1, 1)
    // 判断节点是否有左孩子，因为二叉堆的特性，有右必有左
    while (this.getLeftIndex(k) < this.size()) {
      let j = this.getLeftIndex(k)
      // 判断是否有右孩子，并且右孩子是否大于左孩子
      if (j + 1 < this.size() && this.heap[j + 1] > this.heap[j]) j++
      // 判断父节点是否已经比子节点都大
      if (this.heap[k] >= this.heap[j]) break
      this._swap(k, j)
      k = j
    }
  }
  _swap(left, right) {
    let rightValue = this.heap[right]
    this.heap[right] = this.heap[left]
    this.heap[left] = rightValue
  }
}

8、散列表（Hash）

散列表英文叫 Hash table，也叫哈希表，是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找速度。这个映射函数叫做散列函数，存放记录的数组叫散列表

javascript 中的Object、Set、WeakSet、Map、WeakMap 都是哈希结构

// 哈希表的实现
class HashTable {
  constructor() {
    this.storage = [];
    this.count = 0;
    this.limit = 7; // 默认数组长度
  }

  // 判断是否是质数
  isPrime(num) {
    const temp = Math.floor(Math.sqrt(num));
    for (let i = 2; i <= temp; i++) {
      if (num % i === 0) {
        return false;
      }
    }
    return true;
  }

  // 获取质数
  getPrime(num) {
    while (!this.isPrime(num)) {
      num += 1;
    }
    return num;
  }

  // 哈希函数
  hashFunc(str, max) {
    let hashCode = 0;

    // 霍纳算法
    for (let i = 0; i < str.length; i++) {
      hashCode = hashCode * 37 + str.charCodeAt(i);
    }

    return hashCode % max;
  }

  // 插入数据
  put(key, value) {
    // 通过哈希函数计算数组下标
    const index = this.hashFunc(key, this.limit);
    let bucket = this.storage[index];

    if (!bucket) {
      // 计算得到的下标还未存放数据
      bucket = [];
      this.storage[index] = bucket;
    }

    let isOverwrite = false; // 是否为修改操作

    for (const tuple of bucket) {
      // 循环判断是否为修改操作
      if (tuple[0] === key) {
        tuple[1] = value;
        isOverwrite = true;
      }
    }

    if (!isOverwrite) {
      // 不是修改操作，执行插入操作
      bucket.push([key, value]);
      this.count++;

      // 如果填充因子大于 0.75 需要对数组进行扩容
      if (this.count / this.length > 0.75) {
        const primeNum = this.getPrime(this.limit * 2);
        this.resize(primeNum);
      }
    }
  }

  // 获取数据
  get(key) {
    const index = this.hashFunc(key, this.limit);
    const bucket = this.storage[index];
    if (!bucket) {
      return null;
    }
    for (const tuple of bucket) {
      if (tuple[0] === key) {
        return tuple[1];
      }
    }
  }

  // 删除数据
  remove(key) {
    const index = this.hashFunc(key, this.limit);
    const bucket = this.storage[index];
    if (!bucket) {
      return null;
    }
    for (let i = 0; i < bucket.length; i++) {
      const tuple = bucket[i];
      if (tuple[0] === key) {
        bucket.splice(i, 1);
        this.count -= 1;
        // 如果填充因子小于0.25，需要缩小数组容量
        if (this.count / this.limit < 0.25 && this.limit > 7) {
          const primeNum = this.getPrime(Math.floor(this.limit / 2));
          this.resize(primeNum);
        }
        return tuple[1];
      }
    }
    return null;
  }

  // 重新设置数组长度
  resize(newLimit) {
    const oldStorage = this.storage;
    this.limit = newLimit;
    this.count = 0;
    this.storage = [];
    // 将旧数据从新添加到哈希表中
    oldStorage.forEach((bucket) => {
      if (!bucket) {
        return;
      }
      for (const tuple of bucket) {
        this.put(...tuple);
      }
    });
  }

  isEmpty() {
    return this.count === 0;
  }

  size() {
    return this.count;
  }
}

__EOF__

本文作者：蓝色帅-橙子哥
本文链接：https://www.cnblogs.com/lhl66/p/15411814.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！