Vicinity Vision Transformer概述
0.前言
1.针对的问题
视觉transformer计算复杂度和内存占用都是二次的，这主要是softmax归一化导致的，这使其无法处理高分辨率图像或细粒度图像patch。
2.主要贡献
(1)提出了一种新的线性视觉自注意模型，该模型在线性视觉transformer中引入了基于二维曼哈顿距离的局部性偏差。
(2)提出了一种新的多头自注意模块——邻近注意块，以实现邻近注意所需的假设。该算法包含特征缩减注意力(feature reduction attention, FRA)模块和特征保持连接(feature preserving connection, FPC)模块，以控制计算开销和提高特征提取能力。
(3)构造了邻近视觉Transformer(Vicinity Vision Transformer, VVT)，它作为通用的视觉骨干，易于应用于视觉任务。大量的实验验证了VVT在各种计算机视觉基准上的有效性。
3.方法
1.将softmax替换成一个与序列长度N成线性关系的函数，具体来说就是把相似度函数softmax换成一个可分解的相似度函数
，找到一个核函数φ(ReLU)，使得先算注意力矩阵A=
∈RN×N变为先算φ(K)TV∈Rd×d。2.使序列长度N远大于特征维数。3.利用曼哈顿距离加入局部性偏置。
在NLP领域出现了很多将自注意力进行分解以将其计算复杂度降低为线性的方法，但是这些方法在视觉领域效果不好，作者经过研究认为局部性偏置对于视觉来说是一个很重要的性质，所以作者提出基于相邻图像块测量的二维曼哈顿距离，对每个图像块调整其注意力权重，在这种情况下，相邻的patch会比距离较远的patch获得更强的注意力。也就是论文中的re-weighting机制。
线性化可以通过选取一个可分解的相似函数S(·)来满足来实现，其中φ(·)为核函数。给定这样一个核函数，可以将self-attention模块的输出写为:
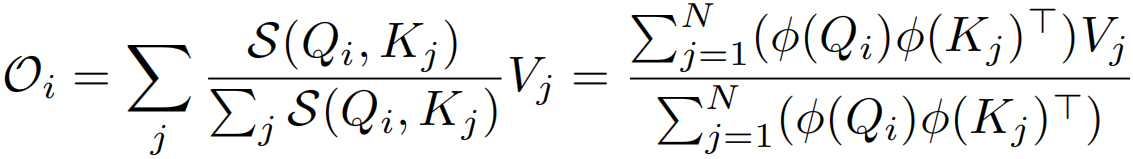
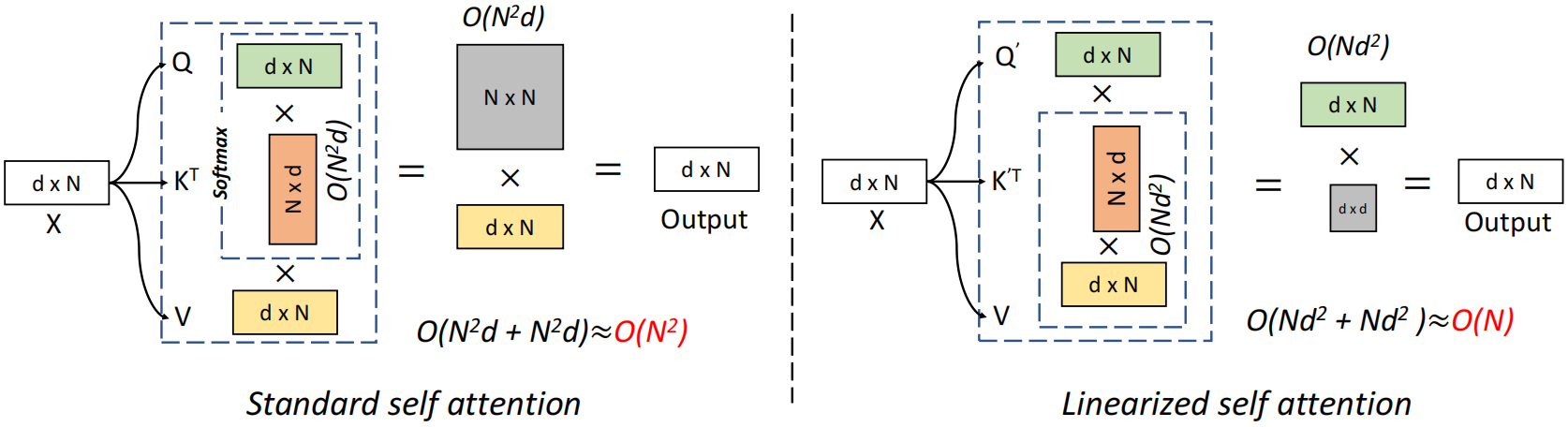
标准自注意力中相似度函数S(·)是softmax函数，输出O=Att(x)=AV，A∈RN×N，时空复杂度关于N都是二次，现在不计算注意力矩阵A∈RN×N，而是先计算φ(K)TV∈Rd×d，即
，使O(N2d)运算转换为O(Nd2)运算
softmax归一化是自注意力算法二次复杂度的根源。线性化的关键在于用另一个相似度函数代替标准的softmax操作。
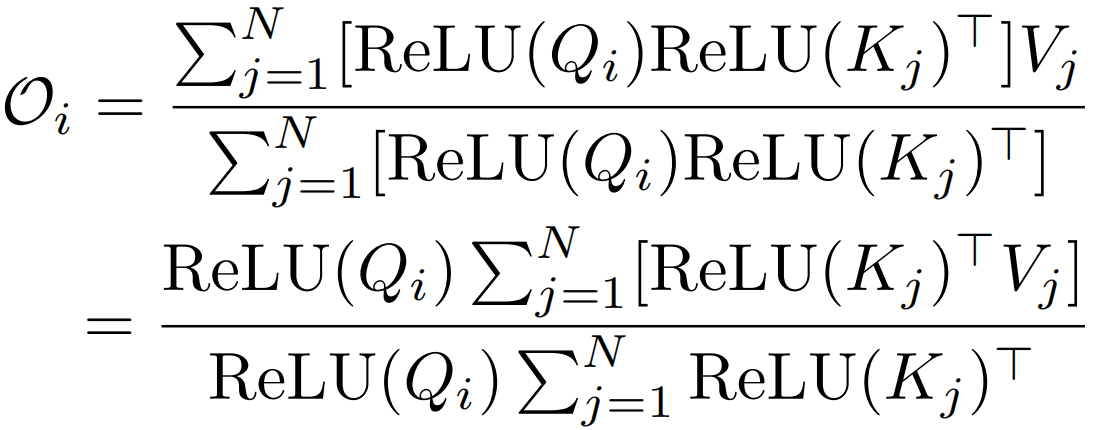
这种方法与序列长度N成线性关系。且保留了标准自注意的两个重要特性:(1)它始终是正的，避免了负相关信息的聚集。(2)所有元素都位于[0,1]之间。
此外，还需要加入局部性偏置，
，G生产距离权重。这里的G不能直接使用欧几里得距离
，因为其不能分解为关于i和j的两项，这里用qi和kj分别代表来自Q和K的一个token，u表示在2D特征图的第几行，r代表列。2D曼哈顿距离虽然可以很容易地解耦到两个方向，
但是绝对值操作依旧无法分解。这里作者假设给定大小为m×n的特征图，通过下面两个等式得到一个可分解的相似度函数S(Qi，Kj)。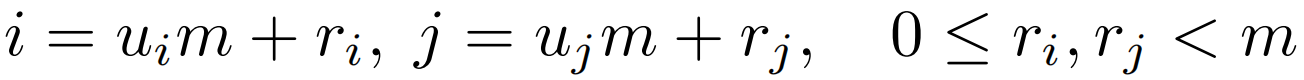
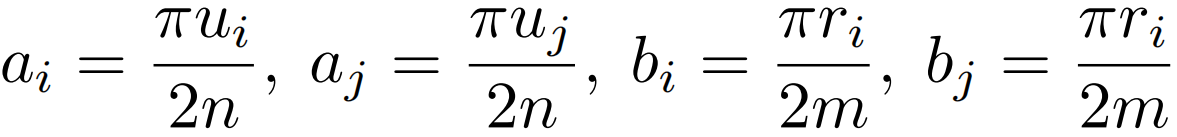
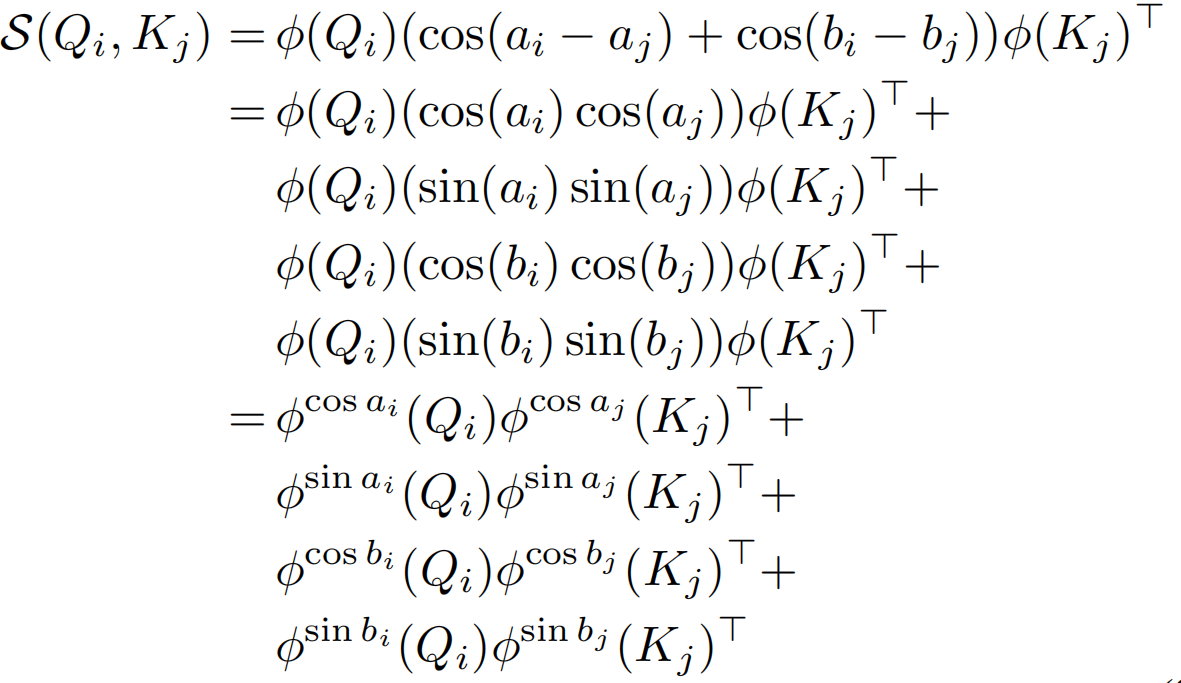
标准自注意力与线性自注意力对比如下：
此外，与基于vanilla transformer的方法相比，当序列长度远大于特征维数时，邻近注意力算法表现出效率优势。为了满足这一要求，本文提出了一种新的邻近注意力块，在不牺牲性能的前提下降低了特征维数。包括一个特征缩减注意力(Feature Reduction Attention, RFA)模块和一个特征保持连接(Feature Preserving Connection, FRC)模块，RFA模块将输入特征维数降低一半，FRC模块恢复原始特征分布并增强表示能力。最后采用金字塔结构的邻近注意力块构造了一个名为邻近视觉Transformer(Vicinity Vision Transformer, VVT)的骨干网络。
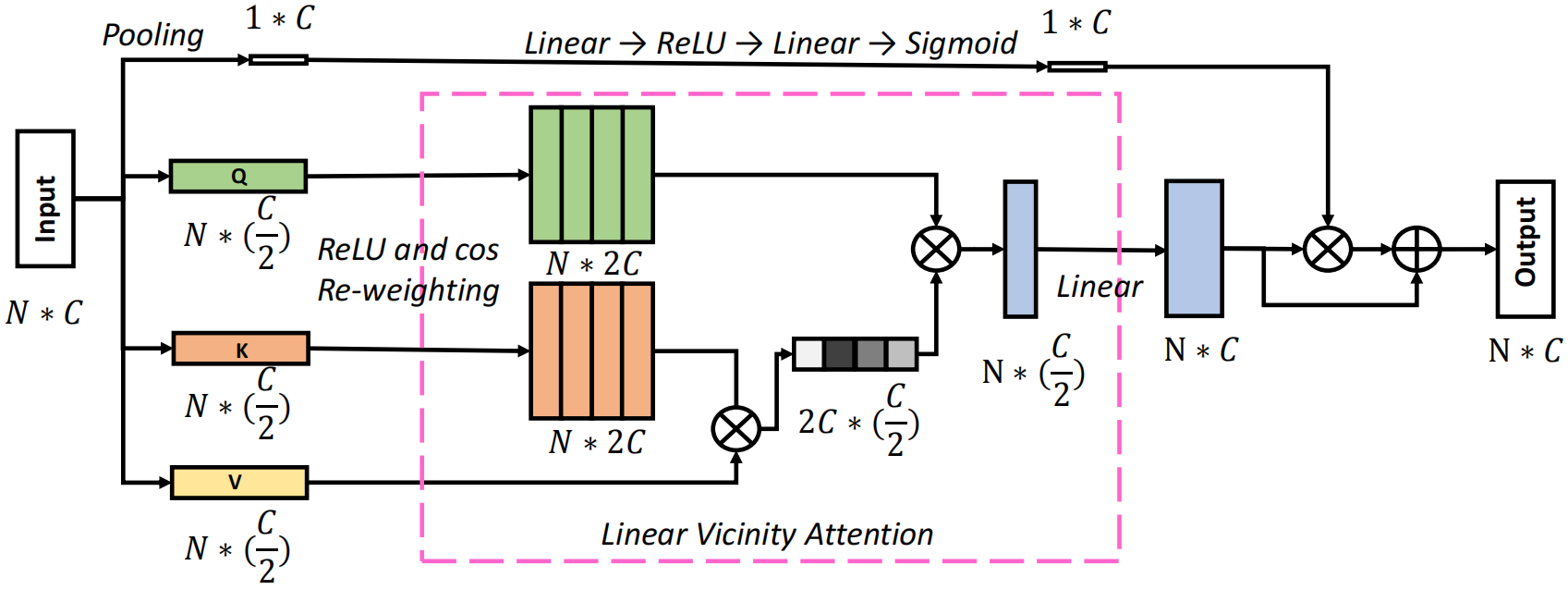
输入X∈RN×d，通过FRA模块将其投影成Q∈RN×d/2, K∈RN×2/d, V∈RN×2/d，并降低了特征维数。然后通过局部分解和re-weighting得到Q'∈ RN×2d, K'∈ RN×2d用于计算线性自注意力，由于自注意力是在更低的维度计算的，在上面添加了一个叫做FRC的跳跃连接，包括一个平均池化操作和两个线性层来保持原始特征分布并增强表示能力。
得到的最终骨干网络如下：
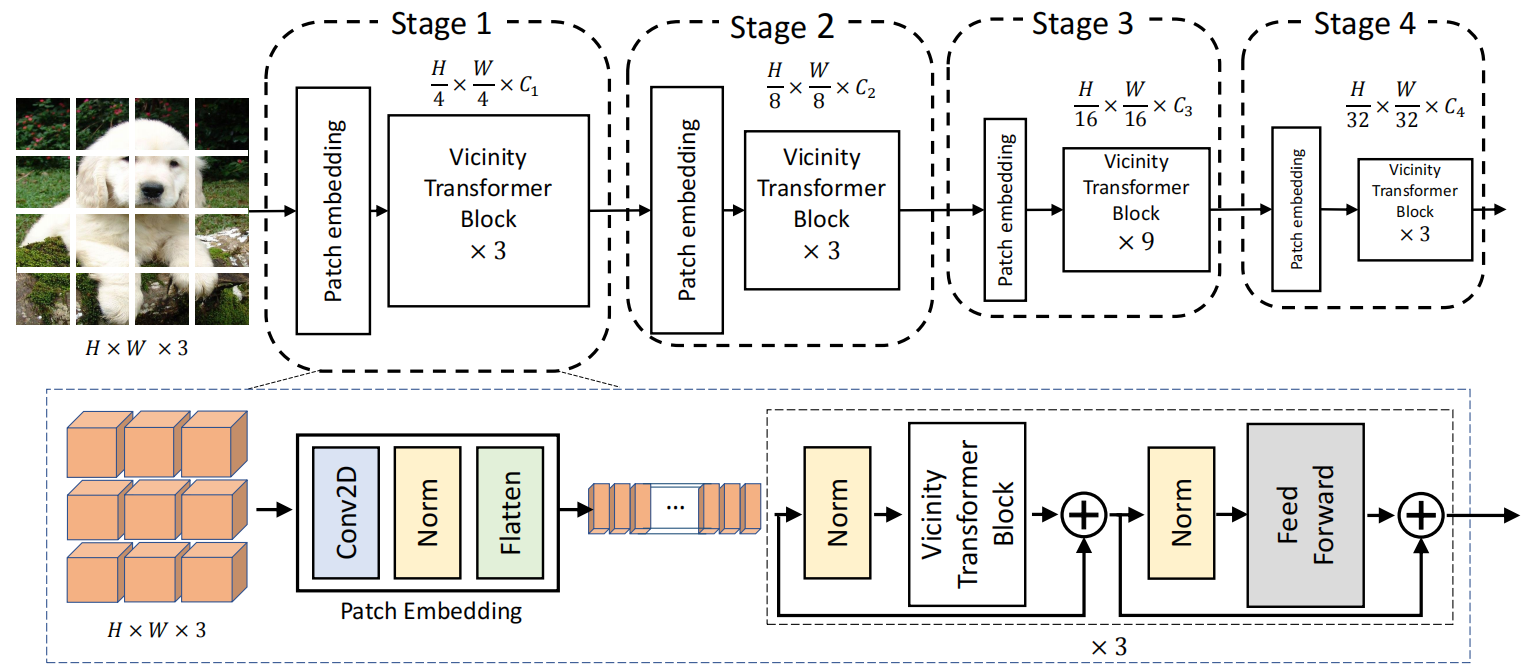
采用渐进式收缩金字塔结构，有四个阶段，生成不同的尺度的特征图。每个阶段包含一个patch embedding层和多个Vicinity Transformer块。
