20171129校内训练

我们把ai向i连边。样例连出来的图是这样的：

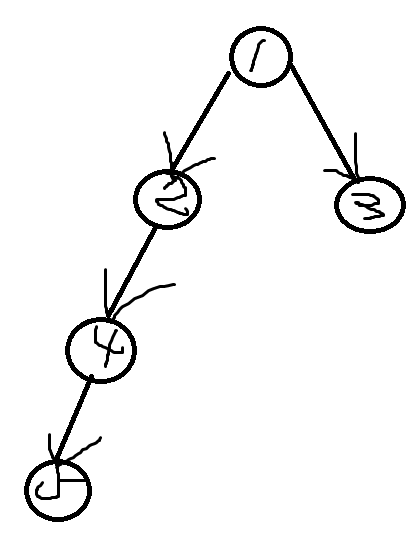
然后，我们可以发现，对于每个节点，它需要和它所有的子节点都比赛一场，然后输给它的父亲节点。

用f[i]表示以i为子树的所有节点全部比赛完需要的最少时间。

如何更新f[i]？第i号节点要和它所有的子节点比赛一场，显然，它应该先和它的子节点所用时间最短的，所用时间第二的......这样打，这样时间不会浪费

即我们把它的子节点的f值排序，用一个变量now记录此时所用时间，遍历每一个节点，若当前节点能打（即它的最少时间<=now），那么就打(now++)，否则只能等到它的最小时间再打(now=f[]+1)。f[i]=now。

注意：在dfs中，这一层递归保存的全局变量容易被后一层的递归保存的给替换。就像这份代码中的：

for(int i=h[x];i;i=nxt[i])dfs(to[i]);
for(int i=h[x];i;i=nxt[i])a[++tot]=f[to[i]];

原先写成for(int i=h[x];i;i=nxt[i]){dfs(to[i]);a[++tot]=f[to[i]];}    a数组就被替换了。

解决办法1：不开全局。2：像这份代码一样，先递归好下一层的，再对这一层的进行操作。

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int q[100100];
int h[101001],nxt[101001],to[101001],k=0;
int f[101001],a[100100];
void ins(int u,int v){nxt[++k]=h[u];to[k]=v;h[u]=k;}
void dfs(int x)
{
    int tot=0;
    for(int i=h[x];i;i=nxt[i])dfs(to[i]);
    for(int i=h[x];i;i=nxt[i])a[++tot]=f[to[i]];
    if(tot==0){f[x]=0;return;}
    sort(a+1,a+tot+1);
    int Max=a[1]+1;
    for(int i=2;i<=tot;i++)if(a[i]+1<=Max)Max++;else Max=a[i]+1;
    f[x]=Max;
}
int main()
{
//    freopen("contest.in","r",stdin);freopen("contest.out","w",stdout);
    int n;scanf("%d",&n);
    for(int i=2;i<=n;i++)
    {
        int a;scanf("%d",&a);
        ins(a,i);
    }
    dfs(1);printf("%d",f[1]);
    return 0;
}

 

首先，根据调和级数，总拍摄点只有大约nlogn个。

对于每个k，我们统计拍不到的植被数，拍不到的植被会被包含在相邻两个拍摄点（开区间）或边界与拍摄点（左开右闭（右开左闭）区间）之间。

即黑色的点为拍摄点，红色的点为边界，黄色的区间就无法被拍到，绿色的区间就能被拍到。

然后，原题转化成，给出m个区间[l,r]，给出一些询问，询问一个区间[a,b]，有多少个区间[l,r]满足l>=a&&r<=b。

简单的二维偏序问题。爱怎么做怎么做。

这是拍不到的植被数，答案为总数-拍不到的植被数

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
struct xxx{
    int l,r,type,id;
}q[2000000],tmp[2000000];
int ans[2000000];
bool cmp(xxx a,xxx b){return a.l!=b.l?a.l>b.l:a.type>b.type;}
void cdq(int l,int r)
{
    if(l==r)return;
    int mid=(l+r)/2;
    cdq(l,mid);cdq(mid+1,r);
    int i=l,j=mid+1,tot=0,sum=0;
    while(i<=mid&&j<=r)
    {
        if(q[i].r<=q[j].r){tmp[++tot]=q[i];sum+=q[i].type;i++;}
        else {ans[q[j].id]+=sum;tmp[++tot]=q[j];j++;}
    }
    while(i<=mid)tmp[++tot]=q[i++];
    while(j<=r){ans[q[j].id]+=sum;tmp[++tot]=q[j++];}
    for(int i=l;i<=r;i++)q[i]=tmp[i-l+1];
}
int main()
{
    freopen("photo.in","r",stdin);freopen("photo.out","w",stdout);
    int n,m,tot=0;scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        tot++;scanf("%d%d",&q[tot].l,&q[tot].r);q[tot].id=0;q[tot].type=1;
    }
    for(int i=1;i<=n;i++)
    {
        int k=1;
        for(;k*i<=n;k++)
        {
            tot++;q[tot].l=(k-1)*i+1;q[tot].r=k*i-1;q[tot].type=0;q[tot].id=i;
        }
        tot++;q[tot].l=(k-1)*i+1;q[tot].r=n;q[tot].type=0;q[tot].id=i;
    }
    sort(q+1,q+tot+1,cmp);cdq(1,tot);
    for(int i=1;i<=n;i++)printf("%d\n",m-ans[i]);
    return 0;
 }