string
写写博客,记记术语,方便以后看题解/hanx。
串串感觉和数据结构、DP 都有藕断丝连的关系,但如果把这些知识点分到其他板块里面就让被硬塞进这些字符串知识点的板块过于割裂,所以干脆单拎出来。
说明:本篇中字符串下标从 0 开始。
Manacher
给一个串,如何求所有的回文半径?
维护覆盖了当前点的右端点最右的回文串,找到当前点关于这个回文串的中心的对称点,直接把它的在这个串内的信息拿到右端点上,剩下的暴力扩展就行了。因为暴力扩展的时候右端点只增不减,所以时间复杂度为 \(\Theta(n)\)。
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1.1e7 + 10;
inline bool chk(char c) { return c >= 'a' && c <= 'z'; }
int n, f[N];
char s[N], c;
int main()
{
s[0] = '~';
while (chk(c = getchar())) s[++n] = '|', s[++n] = c;
s[++n] = '|';
for (int i = 1, maxr = 0, mid = 0; i <= n; i++)
{
if (i < maxr) f[i] = min(f[2 * mid - i], maxr - i);
for (int j = i + f[i] + 1; j <= n; j++)
{
if (s[j] == s[2 * i - j]) ++f[i];
else break;
}
if (i + f[i] > maxr) maxr = i + f[i], mid = i;
}
int ans = 0;
for (int i = 1; i <= n; i++)
if (f[i] > ans) ans = f[i];
cout << ans;
return 0;
}
Trie
这里主要放一些 01-trie 常见的 trick,并写一写可持久化 01-trie。OI-Wiki 写的太烂了,主要参考了这一篇。
tricks
trick 1:最大异或
从高位到低位存储,直接往 01-Trie 里面加数,然后能往另一边走就往另一边走。例题
trick 2:异或和
考虑对答案有贡献当且仅当 1 的个数为奇数,于是从低位到高位存储。
问题来了,如果还让求最大异或该咋办?
答:开两颗呗,卡卡常不就行了?
对于每一位记:
-
c[i]:当前节点到他爸爸这条边被经过的总次数 -
w[i]:当前节点为根的子树内所有边权的异或和
然后就自然地有代码:
void maintain(int u)
{
c[u] = w[u] = 0;
if (ch[u][0])
{
c[u] += c[ch[u][0]]; // 经过他儿子的肯定经过他自己
w[u] ^= (w[ch[u][0]] << 1); // 直接异或就行了,注意要乘二
}
if (ch[u][1])
{
c[u] += c[ch[u][1]];
w[u] ^= ((w[ch[u][1]] << 1) | (c[ch[u][1]] & 1));
// 如果右儿子数量为奇数,说明这一位还能有 1 的贡献,所以直接或上
}
}
然后插入和删除的时候修改当前节点的 w 就行了。代码:
void ins(int &u, int x, int dep)
{
if (!u) u = newnode();
if (dep > MAXH) return w[u]++, void();
ins(ch[u][x & 1], x >> 1, dep + 1);
maintain(u);
}
void del(int u, int x, int dep)
{
if (dep > MAXH) return w[u]--, void();
del(ch[u][x & 1], x >> 1, dep + 1);
maintain(u);
}
trick 3:全局加一
考虑加一的操作等价于把从后往前第一个 0 变成一,然后后面的全部异或,这在 01-trie 上就是从低位到高位维护,不断交换左右儿子,直到找到 0。代码:
void add(int u)
{
swap(ch[u][0], ch[u][1]);
if (ch[u][0]) add(ch[u][1]);
maintain(u);
}
代码中判断 ch[u][0] 是因为你已经交换过一遍左右儿子了。
区间加一就做一遍可持久化就行了。
可持久化 01-Trie
设 \(s_i=\bigotimes\limits_{j=1}^i a_i\),则答案是 \(s_n\otimes s_{p-1}\otimes x\) 的最大值,于是问题就转化成了 \([l-1,r-1]\) 区间内 \(s_p \otimes (s_n\otimes x)\) 的最大值,然后类比可持久化线段树,两个树相减表示区间。
#include <bits/stdc++.h>
using namespace std;
const int N = 6e5 + 5, H = 28;
int n, m, a[N], s[N], rt[N], ch[N * 33][2], cnt[N * 33], tot;
void Insert(int u, int pre, int x)
{
for (int i = H; i >= 0; i--)
{
cnt[u] = cnt[pre] + 1;
int c = ((x & (1 << i)) ? 1 : 0);
if (!ch[u][c]) ch[u][c] = ++tot;
ch[u][c ^ 1] = ch[pre][c ^ 1];
u = ch[u][c], pre = ch[pre][c];
}
cnt[u] = cnt[pre] + 1;
}
int query(int u, int v, int x)
{
int res = 0;
for (int i = H; i >= 0; i--)
{
int c = ((x & (1 << i)) ? 1 : 0);
if (cnt[ch[u][!c]] - cnt[ch[v][!c]]) u = ch[u][!c], v = ch[v][!c], res += (1 << i);
else u = ch[u][c], v = ch[v][c];
}
return res;
}
int main()
{
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr);
cin >> n >> m;
for (int i = 1, x; i <= n; i++) cin >> a[i], s[i] = s[i - 1] ^ a[i];
for (int i = 1; i <= n; i++) rt[i] = ++tot, Insert(rt[i], rt[i - 1], s[i]);
char op;
for (int l, r, val; m; m--)
{
cin >> op;
if (op == 'A')
{
n++, cin >> a[n];
s[n] = s[n - 1] ^ a[n], rt[n] = ++tot;
Insert(rt[n], rt[n - 1], s[n]);
}
if (op == 'Q')
{
cin >> l >> r >> val;
l--, r--;
if (!l) cout << max(s[n] ^ val, query(rt[r], rt[0], s[n] ^ val)) << '\n';
else cout << query(rt[r], rt[l - 1], s[n] ^ val) << '\n';
}
}
return 0;
}
前缀函数与 KMP
这一块 OI-Wiki 讲得还可以,扳回一城。
前缀函数
定义一个长度为 \(n\) 的字符串 \(s\),其前缀函数 \(\pi[i]\) 表示前缀 \(s[1\dots i]\) 中最长的相等的真前缀与真后缀的长度,并规定 \(\pi[0]=0\)。
计算 \(\pi\)
暴力时间复杂度是 \(O(n^3)\) 的,有很大的进步空间——OI Wiki
怎么优化?
随几个串串,把 \(\pi\) 算算,把规律看看,发现相邻的 \(\pi\) 最多增加 1,由此我们可以把长度的枚举上界从 \(i\) 变成 \(\pi[i-1]+1\),这样最好情况下比较的次数是 \(n-1\),而每次最多加一的性质保障增长的比较次数是 \(n-2\),总比较次数就是 \(\Theta(n)\) 的,每次比较时间复杂度为 \(O(n)\),所以总的是 \(O(n^2)\)。
还能不能更优?
考虑当 \(s[i+1]\)!=\(s[\pi[i]]\) 时怎么做。这个时候我们希望长度仅次于 \(\pi[i]\) 的 \(j\) 使位置 \(i\) 的前缀性质得以保证,然后我们比较 \(s[i+1]\) 和 \(s[j]\),如果他们相等,那 \(\pi[i+1]=j+1\),否则以此类推找 \(j^{(2)}\),直到 \(j=0\),如果还不行,就只能 \(\pi[i+1]=0\)。
画个图先:
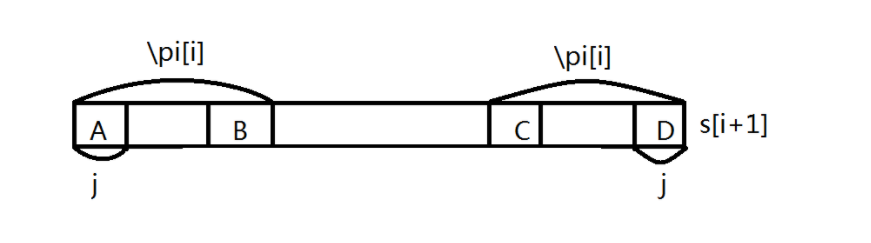
首先我们知道 A 和 D 相同,然后由于 \(pi\) 的性质,A 和 C 相同,B 和 D 想通,也就是 A,B,C,D 都相同,于是有 \(j=\pi[\pi[i]-1]\),然后就可以得出 \(j^{(n)}=\pi[j^{(n-1)}-1]\),这样一步步跳就可以在 \(O(n)\) 的时间求出 \(\pi\),而且这么做是在线的!!!
时间复杂度咋证?
原来 \(O(n^2)\) 是因为比较子串对吧,现在不用比了,不就是 \(\Theta(n)\) 的了?
code:
vector<int> pf(string s)
{
int n = (int)s.length();
vector<int> pi(n);
for (int i = 1; i < n; i++)
{
int j = pi[i - 1];
while (j && s[i] != s[j]) j = pi[j - 1];
if (s[i] == s[j]) j++;
pi[i] = j;
}
return pi;
}
Z 函数(扩展 KMP)
这一块 OI-Wiki 上和 \(\pi\) 函数同级,但两者应用差别小多了,所以放进来了。
对于长度为 \(n\) 的字符串 \(s\),定义 \(z[i]\) 表示 \(s\) 和 \(s[i\dots n-1]\) 的最长公共前缀(LCP)的长度。
考虑如何求。暴力 \(O(n^2)\) 做法就不讲了。考虑线性做法。对于 \(i\),我们称 \([i\dots i+z[i]-1]\) 是 \(i\) 的匹配段,也叫 Z-box。记 \(i+z[i]-1\) 最大的一组 Z-box 为 \([l\dots r]\)。
如果 \(i\leq r\),那么由 \([l,r]\) 的定义,画个图就可以知道\(z[i]\geq \min(z[i-l],r-i+1)\)
-
\(z[i-l]\leq r-i+1\),则 \(z[i]=z[i-l]\);
-
\(z[i-1]>r-i+1\),那么令 \(z[i]=r-i+1\),然后向右暴力扩展。
如果 \(i\geq r\),那么直接向右暴力扩展。要记得在每次求 \(z[i]\) 后更新 \([l,r]\)。
这样做复杂度显然是 \(O(n)\) 的,因为 \(r\) 单调递增。
code:
vector<int> z_function(string s)
{
int n = (int)s.length();
vector<int> z(n);
for (int i = 1, l = 0, r = 0; i < n; i++)
{
if (i <= r && z[i - l] < r - i + 1) z[i] = z[i - l];
else
{
z[i] = max(0, r - i + 1);
while (i + z[i] < n && s[i + z[i]] == s[z[i]]) ++z[i];
}
if (i + z[i] - 1 > r) r = i + z[i] - 1, l = i;
}
return z;
}
应用
Knuth–Morris–Pratt 算法
把被匹配的串和匹配的串拼一块,算一遍 \(\pi\) 就完了。
字符串的周期
对于字符串 \(s\),\(0\leq r<|s|\),如果长度为 \(r\) 的前缀与后缀相等,称 \(r\) 为 \(s\) 的一个 \(\text{border}\)。
由 \(r\) 是 \(s\) 的一个 \(\text{border}\) 可推得 \(|s|-r\) 是 \(s\) 的一个周期,\(n-\pi[n-1]\) 是 \(s\) 的最小周期。
统计每个前缀出现的次数
先考虑前缀在其本身的字符串中出现的次数。首先对于 \(i\),长度为 \(\pi[i]\) 的前缀一定出现了一次,并且在 \(i\) 作为右端点的位置上不存在更长的,更短的就是 \(j^{(n)}\),倒着加贡献就行了,最后别忘了它本身。code:
vector<int> ans(n + 1);
for (int i = 0; i < n; i++) ans[pi[i]]++;
for (int i = n - 1; i >= 0; i--) ans[pi[i - 1]] += ans[i];
for (int i = 0; i < n; i++) ans[i]++;
然后考虑前缀在另一个字符串中出现的次数,类比 \(\text{kmp}\),直接接一块跑上面的就行。
一个字符串中本质不同的子串个数
迭代地考虑问题,考虑把字符一个个往串里加怎么更新答案。令当前的答案为 \(k\),新加的字符为 \(c\),原来的串是 \(s\),令 \(t=sc\),\(t\sim\) 表示 \(t\) 倒过来之后的字符串。我们发现 \(c\) 对答案的贡献就是 \(t\sim\) 中只出现过一次的前缀个数,易知这个就是 \(|s|+1-\pi_{\max}\),这个是 \(O(n^2)\) 的,因为反转之后新加的就跑最前面去了,而你并不会一个类似后缀函数的东西怎么动态算,所以只能 \(O(n^2)\)。(但是这个东西真的可以好好想想,挺有价值的。)
当然,你还可以把前缀函数建出一个自动机,但这个后面再说(或者永远不说)。
自动机
OI 中所说的“自动机”一般都指“确定有限状态自动机”,也就是 \(\text{dfa}\),是计算机科学中常见的数学模型,对于学习 \(\text{kmp}\) 等算法有帮助理解的作用。
写这一部分的时候主要参考了 qyc 在 SDSC2024 的讲义以及 qyc 的博客。
dfa 是什么
感性理解,\(\text{dfa}\) 是一个有向图,用来识别信号序列。信号序列指的是一连串有序的信号。
形式化地,一个 \(\text{dfa}\) 由一下五部分组成:
- 字符集 \(\Sigma\),该自动机只能输入这些字符。
- 状态集合 \(Q\)。如果把 \(\text{dfa}\) 看成一个有向图,那么一个状态就是有向图上的一个顶点。
- 起始状态 \(start,start\in Q\)。可以理解为有向图上入度为 0 的一个点。
- 接受状态集合 \(F\)。可以理解为有向图上出度为 0 的一组点。
- 转移函数 \(\delta\)。当前状态是如何到下一个状态的,可以理解为有向图上的边。
如果 \(\text{dfa}\) \(A\) 能识别字符串 \(S\),那么 \(A(S)=\text{True}\),否则 \(A(S)=\text{False}\)。
如果一个 \(\text{dfa}\) 读入一个字符串是,这个字符串沿着它走能走到接受状态集合,那么说这个字符串被这个 \(\text{dfa}\) 接受,否则说这个 \(\text{dfa}\) 不接受 这个字符串。
如果一个状态 \(v\) 没有字符 \(c\) 的转移,那么令 \(\delta(v,c)=\text{null}\),而 \(\text{null}\) 只能转移到 \(\text{null}\)。
我们扩展定义 \(\delta\),令 \(\delta(v,s)=\delta(\delta(v,s[0]),s[1\dots n-1])\),那么 \(A(s)=[\delta(start,s)\in F]\)。
\(\text{dfa}\) 的一个好处就是一个串前面的所有信息都可以被一个节点概括,于是可以做 \(\text{dp}\) 的时候把 \(\text{dfa}\) 的状态作为状态中的一维。
dfa 的笛卡尔积
如果有两个 \(\text{dfa}\),我们可以构造一个状态集合为两个 \(\text{dfa}\) 的状态集合的笛卡尔积,它的每个状态表示“在两个 \(\text{dfa}\) 上分别在某个状态”,转移在两个 \(\text{dfa}\) 上分别维护。
\(\text{nfa}\) 是指可以有多个相同的转移的 \(\text{dfa}\),也就是说走到这里会有好几个分支,只要一个到了接收状态,那这个串就是被接受的。给定 \(\text{nfa}\),我们可以唯一确定一个状态数为 \(2^n\) 的 \(\text{dfa}\)。
dfa 最小化
这里的最小化指的是规模上的最小化。
如果两个状态的所有转移都是对应相同的,称这两个状态等价。我们尝试把这两个状态合并起来。
朴素的做法就是把每个状态的转移 \(\text{Hash}\) 起来,然后不断合并,直到不能合并。时间复杂度 \(O(n^2\Sigma)\)。
考虑一个更快的方法。既然合并慢,那就分裂。我们在一开始把接受状态合并起来,把拒绝状态合并起来,考虑如果两个状态的同一转移指向了不同的等价类,那么就把这两个状态分裂开。这个算法叫做 \(\text{moore}\) 算法,期望复杂度 \(O(n(\Sigma+\log n))\),但是如果 \(\text{dfa}\) 是一条链,构造使得这些点顺次分裂,每次检查就是 \(O(n^2\Sigma)\) 的。
类似于 SPFA 优化 Bellman-Ford,我们维护一个队列,把每一次分裂后新增的等价类放进去。关键的优化是,我们把一个等价类 \(x\) 分裂成 \(y,z\) 时,可以直接把 \(y,z\) 中较小的放进去,另外一个扔掉。这是因为现有的等价类肯定不会被 \(x\) 分裂了,所以每个等价类到 \(x\) 的情况都是相同的,若能分裂,只用判 \(y,z\) 中任意一个是否一样就行了,不影响正确性,于是时间复杂度就是 \(O(n\Sigma\log n)\) 的。
常见自动机
AC 自动机
就是在 trie 上 kmp。每个节点维护 fail 指针指向 trie 上最深的点满足它是当前点所代表的串的前缀。
namespace acam
{
const int SIZ = 2000005;
struct node
{
int ch[26], fail, ans, id;
node() { memset(ch, 0, sizeof(ch)), ans = id = 0; }
inline int &operator[](const int x) { return x < 26 ? ch[x] : ch[x - 'a']; }
inline int operator[](const int x) const { return x < 26 ? ch[x] : ch[x - 'a']; }
} tr[SIZ];
int tot, ans[SIZ], pcnt;
vector<int> fail[SIZ];
inline void insert(char *s, int &id)
{
int u = 0;
for (int i = 1; s[i]; i++)
{
if (!tr[u][i]) tr[u][i] = ++tot;
u = tr[u][i];
}
if (!tr[u].id) tr[u].id = ++pcnt;
id = tr[u].id;
}
inline void build()
{
queue<int> q;
for (int i = 0; i < 26; i++)
if (tr[0][i]) q.push(tr[0][i]), fail[0].push_back(tr[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
{
if (tr[u][i])
{
tr[tr[u][i]].fail = tr[tr[u].fail][i];
fail[tr[tr[u].fail][i]].push_back(tr[u][i]);
q.push(tr[u][i]);
}
else tr[u][i] = tr[tr[u].fail][i];
}
}
}
void query(char *t)
{
int u = 0;
for (int i = 1; t[i]; ++i) u = tr[u][t[i]], tr[u].ans++;
}
void dfs(int u)
{
for (int v : fail[u])
{
dfs(v);
tr[u].ans += tr[v].ans;
}
ans[tr[u].id] = tr[u].ans;
}
}; // namespace acam
子序列自动机
子序列自动机是接受且仅接受一个字符串的子序列的自动机。构造方式:
-
状态 \(i\) 表示 \(s[1\dots i]\) 的子序列与 \(s[1\dots i-1]\) 的子序列的差集。
-
自动机上每个状态都是接受状态。
-
转移 \(\delta(u,c)=\min\{i|i>u,s[i]=c\}\)。
构造的时候从后往前扫描,时间复杂度 \(O(n|\Sigma|)\)。
Suffix Array
后缀数组 \(sa[i]\) 表示所有后缀排序之后第 \(i\) 大的后缀,另外有数组 \(rk[i]\) 表示第 \(i\) 个后缀的排名为 \(rk[i]\)。它们满足 \(sa[rk[i]]=rk[sa[i]]=i\)。
求 SA
比较通用的做法是利用倍增,时间复杂度 \(O(n\log n)\),好写但是容易被卡,于是我根本没学。
DC3 Algorithm
参考了 应该是发现者的论文。
DC3 Algorithm 是用来求后缀数组的 \(O(n)\) 算法,跑得要比倍增 \(O(n\log n)\) 快,但是常数较大并且不好实现。
自然的想法是把串二分,但是最好也只是 \(O(n\log n)\),于是考虑另外一种分治方法。将起始坐标 \(i\bmod 3=0\) 的归为一类,称为 A 类后缀,其余的归为另一类,称为 B 类后缀。整个的思路是先排 B 类后缀,然后排 A 类后缀,最后归并起来。
第一步,求解 B 类后缀,对于每个后缀用前三个字符进行比较,也就是做三轮基数排序,如果比出来了就结束,否则用以 \(i\) 开头的 6 个字符进行比较。生做肯定会爆掉,于是把字符串重排,把 \(i\bmod 3=1\) 的按排出来的顺序拼在一起,中间加上一个 0 隔开,然后把 \(i\bmod 3=2\) 的按排出来的顺序拼在一起,接在新串最后,然后递归计算,这样就可以六个六个排了。
第二步,求解 A 类后缀,发现 A 类后缀是由一个 A 类字符和一个 B 类后缀构成的,于是以当前字符为第一关键字,B 类后缀为第二关键字再做基数排序就行了。
第三步,将 A 与 B 归并起来。假设归并到 A 的下标为 \(i\),B 的下标为 \(j\),如果 \(s[i]\not=s[j]\),那很愉快,否则分类讨论,如果 \(j\bmod 3=1\),那么 \(j+1\) 与 \(i+1\) 都是 B 类,它们的顺序我们已经求过;如果 \(j\bmod 3=2\),那么 \(j+1\) 与 \(i+1\) 的类别正好反过来,可以转化为上一种情况。
这样通过巧妙的三步,我们就可以求出 \(sa\)。
如何证明时间复杂度?
有递归式 \(T(n)=\Theta(n)+T(\frac{2}{3}n)\),运用 Master Theorem 可得 \(T(n)=\Theta(n)\)。
SA-IS
参考了 A Walk Through the SA-IS Algorithm。
这也是一种 \(O(n)\) 求后缀数组的方法,但是常数要比 DC-3 小,跑起来会更快,但是难写难理解,所以用处不如 DC3。
记 \(S(i)\) 表示以 \(i\) 为起点的后缀,定义 \(S(i)<S(i+1)\) 的后缀为 S-type 后缀,定义 \(S(i)>S(i+1)\) 的后缀为 L-type 后缀。 容易知道每个后缀的类型可以从后往前推,并且对于两个后缀,如果它们的起始字符是一样的,那么 S-type 的要比 T-type 的大。
定义一种特殊的 S-type 后缀 lm-type 后缀表示一连串的 S-type 后缀中最左边的那个。定义 LMS 子串表示位置相邻的两个 lm-type 后缀的起始位置之间的所有字符(不包括第二个 lm-type 后缀的起始字符)。容易知道所有 LMS 子串的数量不超过 \(|S|/2\),其长度之和为 \(O(|S|)\)。比较 LMS 子串的方式就是以起始字符为第一关键字,以第二个字符的 Type 为第二关键字。并且可以证明对任意两个 LMS 子串,不存在一个 LMS 子串是另一个 LMS 子串的真前缀。于是我们可以利用基数排序在 \(O(|S|)\) 的时间复杂度内排序,但这没啥用。
我们可以先把 lm-type 的东西排出来,然后用顺序重命名它,放在新串 \(s1\) 中,得到后缀数组 \(sa'\)。
我们需要意识到的是让问题变难的正是这些 lm-type 后缀,所以我们先假设这些后缀已经被排好了,得到的后缀数组为 \(sa'\)。然后我们运用 诱导排序 的方法排序。注意到同种字符开头的排序后肯定放在了一块,并且其内部是 L-type 在前,S-type 在后,于是利用桶排序的思想,记录每种字符的出现次数,并且在 sa 中分配相应的空间,相当于是拿 sa 开了个桶。先倒序扫描 \(sa'\),把 LMS 后缀逆序放入 sa 中对应的 S 型桶中,然后正序扫描 sa,如果 \(sa[i]-1\) 是 L-type,那么将 \(sa[i]-1\) 放入 L 型桶中。然后再倒序扫描 sa,如果 \(sa[i]-1\) 是 S-type,那么将 \(sa[i]-1\) 放入 S 型桶中。
然后需要考虑 LMS 子串的排序。鸡排是可以的,但是常数太大,为了展现 SA-IS 的优越性,仍然使用诱导排序。然后就做完了。
有递归式 \(T(n)=\Theta(n)+T(\frac{n}{2})\),运用 Master Theorem 可得 \(T(n)=\Theta(n)\)。
效率比较
在 LOJ #111 后缀排序 的提交记录中,\(O(n\log n)\) 做法跑了 654ms,DC3 开 O2 跑了 348ms,SA-IS 开 O2 跑了 383ms,可以得出 DC3 在实际应用中的性价比还是很高的。
height 数组
定义两个字符串 \(S\) 和 \(T\) 的 LCP 表示它们的最大公共前缀。在一个字符串 \(S\) 中定义 \(\operatorname{lcp}(i,j)\) 表示后缀 \(i\) 与 \(j\) 的 LCP 的长度。
定义 height 数组 \(height[i]=\operatorname{lcp}(sa[i],sa[i-1])\),并将 \(height[0]\) 视作 0。
引理:\(height[rk[i]]\geq height[rk[i-1]]-1\)
\(\text{proof.}\)
当 \(height[rk[i-1]]\leq 1\) 时,\(\text{RHS}\le 0\),上式显然成立。
当 \(height[rk[i-1]]>1\) 时,根据 height 的定义,有 \(\operatorname{lcp}(sa[rk[i-1]],sa[rk[i-1]-1])>1\),也就是说后缀 \(i-1\) 和后缀 \(sa[rk[i-1]-1]\) 有长度为 \(height[rk[i-1]]\) 的公共前缀。不放记这个前缀为 \(aA\),将后缀 \(i-1\) 表示成 \(aAB\),将后缀 \(sa[rk[i-1]-1]\) 表示成 \(aAD\),那么后缀 \(i\) 就是 \(AB\),并存在后缀 \(SA[rk[i-1]-1]+1\) 为 \(AD\)。
可知 \(AD\leq 后缀 sa[rk[i]-1]\leq AB\),显然后缀 \(i\) 和后缀 \(sa[rk[i]-1]\) 有公共前缀 A。于是结论成立。\(\square\)
于是利用上面的引理,可以 \(O(n)\) 求 height 数组。
for (int i = 0, k = 0; i < n; i++)
{
if (!rk[i]) continue;
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
height[rk[i]] = k;
}
LCP Theorem
有 LCP Lemma:
可利用其推出 LCP Theorem:
感性理解一下就是 height 数组一直大于的一个数就是反复出现的前缀。
利用 LCP Theorem,可以将子串公共前缀问题转化为 RMQ 问题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号