四边形不等式优化 DP

四边形不等式

对 \(w_{i,j}\)，若 \(\forall a \leq b \leq c \leq d,w_{a,d}+w_{b,c}\geq w_{a,c}+w_{b,d}\) ，则称 \(w\) 满足四边形不等式关系，该不等式为四边形不等式。

几何意义

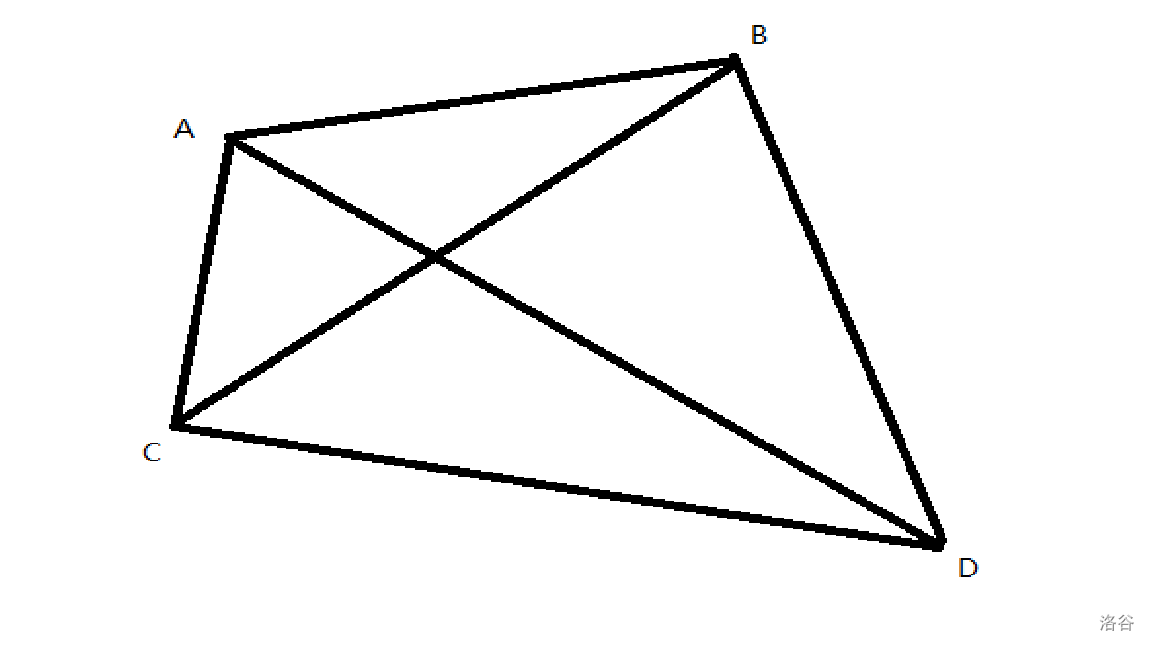
可以由三角形不等式证出凸四边形 \(ABCD\) 中，\(AD+BC \geq AB+CD\)，这就是四边形不等式的几何意义。

性质

满足 \(w_{i,j+1}+w_{i+1,j} \geq w_{i,j}+w_{i+1,j+1}\) 的 \(w\) 满足四边形不等式关系。

证明：

记上式为（1）式。用 \(i+1\) 改写（1）式，得到：\(w_{i+1,j+1}+w_{i+1,j+1}\geq w_{i+1,j}+w_{i+2,j+1}\)，记为（2）式。两式相加，得到：\(w_{i,j+1}+w_{i+1,j} \geq w_{i,j}+w_{i+2,j+1}\)；用 \(i+2\) 改写（1）式，同理可得 \(w_{i,j+1}+w_{i+3,j}\geq w_{i,j}+w_{i+3,j+1}\)，以此类推，我们可以得到 \(w_{a,c+1}+w_{b,c}\geq w_{a,c}+w_{b,c+1}\)，我们用同样的方式就可以推出对 \(a,b,c,d\) 不等式都是正确的，得证。

这个性质多用于证明 \(w\) 满足四边形不等式关系，但我们一般打个表出来，观察到符合性质就直接写优化了。这并不严谨，但场上很好用。

优化 DP

一般地，四边形不等式用来优化形如 \(f_{i}=\min/\max_{j=1}^{i-1}\{f_{j}+v_{j,i}\}\) 的 DP 转移。 下面我们以 \(\min\) 为例说明四边形不等式优化 DP 的过程。

我们引入决策的概念。\(i\) 的决策点 \(p_i\) 表示 \(f_j+v_{j,i}\) 的最值取到的那个点，即 \(\min\limits_{j=1}^{i-1}\{f_j+v_{j,i}\}=f_{p_i}+v_{p_i,i}\)。考虑如何利用决策点与四边形不等式的性质进行优化。

性质1

若 \(v\) 满足四边形不等式关系，则决策点单调。

证明：反证法。若决策点不单调，即存在 \(c,d\) 使 \(b=p_c > p_d=a\)，此时 \(a < b \le c < d\)，根据最优化条件，\(v_{a,d} \leq v_{b,d}\) 且 \(v_{a,c} > v_{b,c}\)，故 \(v_{a,d}-v_{b,d}\le 0 < v_{a,c}-v_{b,c}\)，与四边形不等式矛盾。\(\square\)

性质2

若有 \(x<j\)，存在 \(i>j\) 使 \(j\) 比 \(x\) 更优，则对于 \(i' > i\)，取 \(j\) 比 \(x\) 同样更优。观察到性质1这条性质的特例。一定要注意 \(x<j\) 这个条件。

证明：由题意得 \(f_{x}+v_{x,i} > f_j+v_{j,i}\)，

由四边形不等式有 \(v_{x,i'}+v_{j,i}> v_{x,i}+v_{j,i'}\)

移项得 \(v_{x,i'}-v_{x,i}>v_{j,i'}-v_{j,i}\)

与第一个式子相加，得 \(f_x+v_{x,i'}>f_{j}+v_{j,i'}\)，\(\square\)

具体操作

三元组 \((l,r,c)\) 表示区间 \([l,r]\) 的决策点是 \(c\)。开一个维护 \((l,r,c)\) 三元组的关于 \(c\) 的单调队列，每一次询问 \(p\) 时二分查找就行了。