联合权值

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

输入输出样例

输入样例#1： 

5  

1 2  

2 3

3 4  

4 5  

1 5 2 3 10

输出样例#1： 

20 74

说明

 

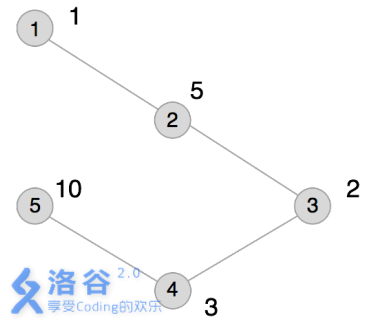
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

noip2014提高组day1第二题

------------------------------------------------------------------------------------------------------------------------------------------------

讲解：

对于这题，最烦的一点是两点之间的距离为2，这意味着不能直接搜，但是我们可以找一个中转站i，设与i相连的点编号分别为

1、2、3……，点1的权为w1，那么所产生的联合权值S=(w1*w2+w1*w3+w1*w4+w2*w3+w2*w4+w3*w4)*2(因为是有序点对)

所以S=(w1+w2+w3+w4)*(w1+w2+w3+w4)-w1*w1-w2*w2-w3*w3-w4*w4我们只需要统计点1、2、3、4的权的和sum和权的平

方和的差就是i点所连的点产生的联合权值，最后求S的和即为联合权值的总和。

 

对与最大值，我们可以在每条边所连接的两点互相更新最大和次大值，再把每个点的两个值相乘的最大值

代码实现：

#include<iostream>
#include<cmath>
#include<algorithm> 
#include<cstdio>
using namespace std;
const int p=10007;//取余 
int n,a[200010],b[200010][2],sum[200010][2],maxn[200010][3],ans,maxx;
void ff(int x,int y)
{
    maxn[x][2]=a[y];
    sort(maxn[x],maxn[x]+3);
    maxn[x][0]=maxn[x][2];
    //maxn[x][1]=maxn[x][1];
    maxx=max(maxx,maxn[x][0]*maxn[x][1]);//更新总的最大值 
   //-----------------------------------------------------------------------
    sum[x][0]=(sum[x][0]+a[y])%p;
    sum[x][1]=(sum[x][1]+a[y]*a[y])%p;
    //连接两条边时一起统计（w1+w2+w3+...+wn）*(w1+w2+w3+...+wn)和(w1*w1+w2*w2+w3*w3+...wn*wn)的值 
    return;
}
int main()
{
    int i,j;
    scanf("%d",&n);
    for(i=1;i<=n-1;i++) scanf("%d%d",&b[i][0],&b[i][1]);
    for(i=1;i<=n;i++) scanf("%d",&a[i]);
    for(i=1;i<=n-1;i++) 
    {
        ff(b[i][0],b[i][1]);
        ff(b[i][1],b[i][0]);//对这条边的两点互相统计最大和次大值  总和 
    }
    for(i=1;i<=n;i++) ans=(ans+sum[i][0]*sum[i][0]-sum[i][1])%p;//总和 
    cout<<maxx<<" "<<ans;
    return 0;
}