c++中二叉树的先序中序后序遍历

c++中二叉树的先(前)序、中序、后序遍历 讲解版

 

首先先看一个遍历的定义（源自度娘）：

所谓遍历(Traversal)，是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。当然遍历的概念也适合于多元素集合的情况，如数组。

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次。树的3种最重要的遍历方式分别称为前序遍历、中序遍历和后序遍历。以这3种方式遍历一棵树时，若按访问结点的先后次序将结点排列起来，就可分别得到树中所有结点的前序列表、中序列表和后序列表。相应的结点次序分别称为结点的前序、中序和后序。

--------------------------------------------------------------------------------------------------------------------------

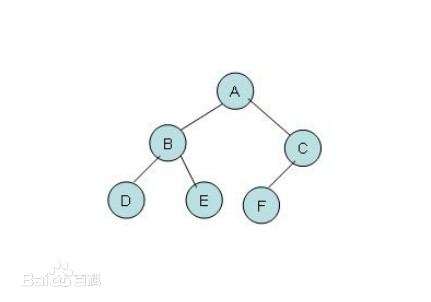
当然，百度上给的解释太专业，先看一个图：

这是一颗二叉树，它的遍历。首先你要明确树的基本组成：根结点、叶结点、父结点、子结点。

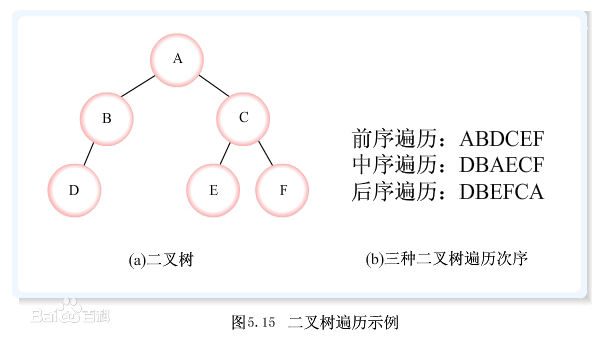
前序遍历：

前序遍历（DLR），是二叉树遍历的一种，也叫做先根遍历、先序遍历、前序周游，可记做根左右。前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。

前序遍历就是类似dfs的方式，从根结点一直从左子树向下直到叶结点，然后返回到叶结点的父亲，再从其父结点的右子树向下。

中序遍历：

中序遍历（LDR）是二叉树遍历的一种，也叫做中根遍历、中序周游。在二叉树中，先左后根再右。巧记：左根右。

中序遍历是先访问左儿子---父亲---右儿子。

后序遍历：

后序遍历（LRD）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中，先左后右再根。巧记：左右根。

后序遍历是先访问左儿子---右儿子---父亲。

---------------------------------------------------------------------------------------------------------------------------------

总结：

其实这三种遍历方法差不了太多，前中后的意思是父结点的访问顺序不一样，只是最后结果有些差别，没有什么特别需要这三种方法的题。只是输入输出和程序中为了方便而起的名字。

 

 

小练习：

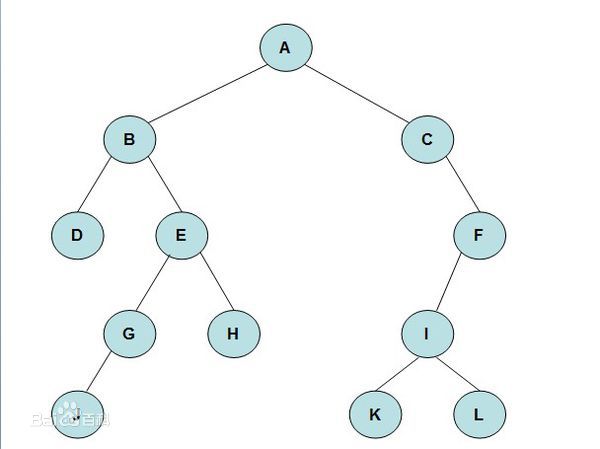
对于这个图，它的

前序遍历：A---B---D---E---G---J---H---C---F---I---K---L

中序遍历：D---B---J---G---E---H---A---C（f为右结点）---K---I---L---F

后序遍历：D---J---G---H---E---B---K---L---I---F---C---A