Halcon 解方程(solve_matrix)
在Halcon中使用solve_matrix解直线方程:
dev_update_off() dev_close_window () Size := 500 dev_open_window (0, 0, Size, Size, 'white', WindowHandle) * 创建随机点 X := [25:50:Size] Y := 15 + 0.4 * X + 0.001 * X * X Y := Y + 40 * rand(|Y|) * 显示随机点 gen_cross_contour_xld (Cross, Size - Y, X, 15, rad(45)) dev_set_color('blue') dev_display(Cross) * 解直线方程 * f(x) = kx + b create_matrix (|X|, 2, 1.0, MatrixA) create_matrix (|X|, 1, X, MatrixACol) set_sub_matrix (MatrixA, MatrixACol, 0, 0) create_matrix (|X|, 1, Y, MatrixB) solve_matrix (MatrixA, 'general', 0, MatrixB, MatrixX) get_value_matrix (MatrixX, 0, 0, K) get_value_matrix (MatrixX, 1, 0, B) Sequence := [0:1200] Distances := K * Sequence + B * 显示拟合直线 gen_contour_polygon_xld (Contour, Size - Distances, Sequence) dev_set_color('green') dev_display(Contour) stop()
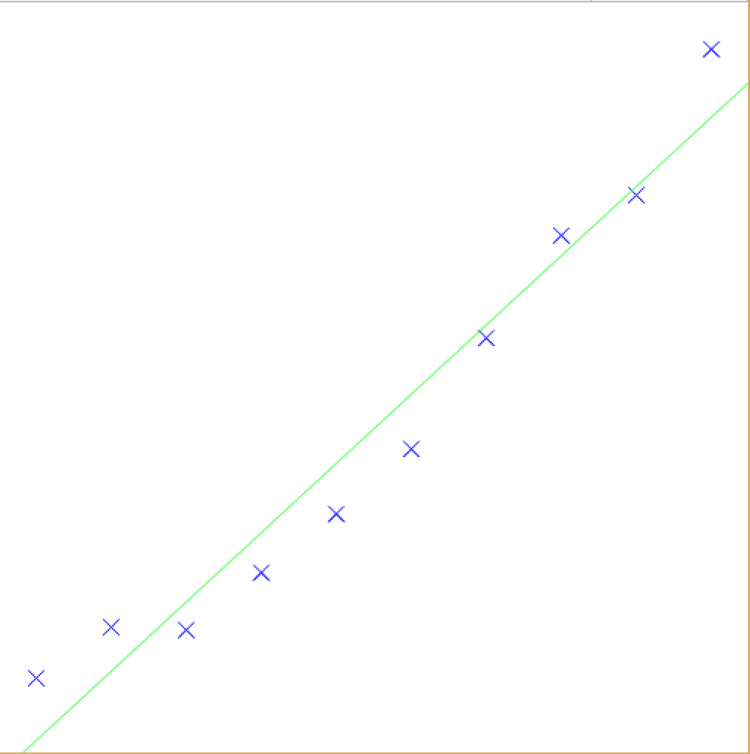
使用solve_matrix解曲线方程:
dev_update_off() dev_close_window () Size := 500 dev_open_window (0, 0, Size, Size, 'white', WindowHandle) * 创建随机点 X := [25:50:Size] Y := 15 + 0.4 * X + 0.001 * X * X Y := Y + 40 * rand(|Y|) * 显示随机点 gen_cross_contour_xld (Cross, Size - Y, X, 15, rad(45)) dev_set_color('blue') dev_display(Cross) * 解曲线方程 * f(x) = a*x^2 + b*x + c create_matrix (|X|, 3, 1.0, MatrixA) create_matrix (|X|, 1, X, MatrixACol1) create_matrix (|X|, 1, X * X, MatrixACol0) set_sub_matrix (MatrixA, MatrixACol1, 0, 1) set_sub_matrix (MatrixA, MatrixACol0, 0, 0) create_matrix (|X|, 1, Y, MatrixB) solve_matrix (MatrixA, 'general', 0, MatrixB, MatrixX) get_value_matrix (MatrixX, 0, 0, A) get_value_matrix (MatrixX, 1, 0, B) get_value_matrix (MatrixX, 2, 0, C) Sequence := [0:1200] Distances := A * Sequence * Sequence + B * Sequence + C * 显示拟合曲线 gen_contour_polygon_xld (Contour, Size - Distances, Sequence) dev_set_color('green') dev_display(Contour) stop ()
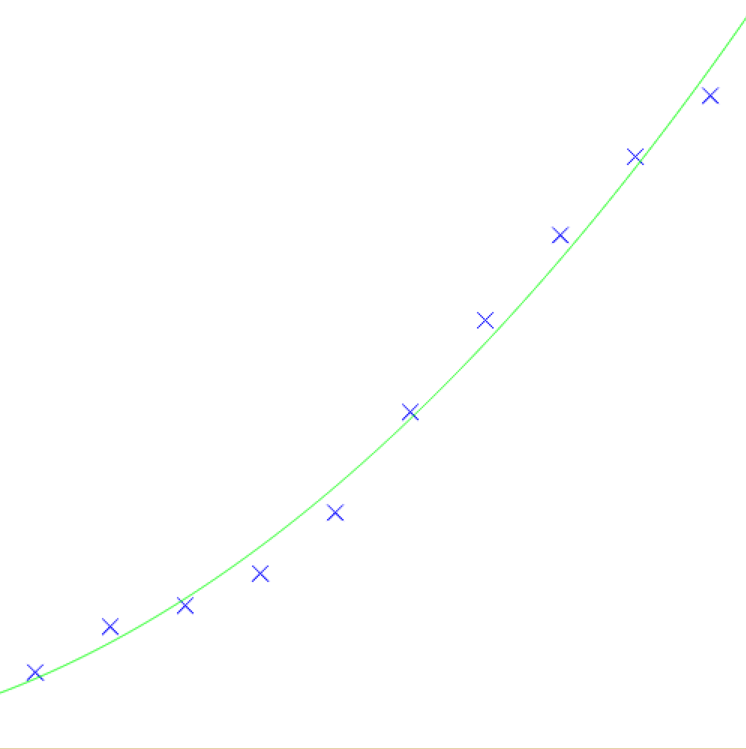
下面是解平面方程:
dev_update_off() dev_close_window () Size := 500 dev_open_window (0, 0, Size, Size, 'white', WindowHandle) * 创建随机点 X := rand(1000) * 100 Y := rand(1000) * 100 Z := rand(|X|) * 6 * 解平面方程 * f(x,y) = ax + by + c create_matrix (|X|, 3, 1.0, MatrixA) create_matrix (|X|, 1, Y, MatrixACol1) create_matrix (|X|, 1, X, MatrixACol0) set_sub_matrix (MatrixA, MatrixACol1, 0, 1) set_sub_matrix (MatrixA, MatrixACol0, 0, 0) create_matrix (|X|, 1, Z, MatrixB) solve_matrix (MatrixA, 'general', 0, MatrixB, MatrixX) get_value_matrix (MatrixX, 0, 0, A) get_value_matrix (MatrixX, 1, 0, B) get_value_matrix (MatrixX, 2, 0, C) PlaneX := [] PlaneY := [] for I := 0 to 99 by 1 PlaneX := [PlaneX, gen_tuple_const(100, I)] PlaneY := [PlaneY, [0:99]] endfor PlaneZ := A * PlaneX + B * PlaneY + C * 三维显示 dev_open_window (0, 0, Size, Size, 'white', WindowHandle) gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D1) gen_object_model_3d_from_points(PlaneX, PlaneY, PlaneZ, ObjectModel3D2) PoseVis := [-50, 0, 2000, 80, 0, 0, 0] visualize_object_model_3d(WindowHandle, [ObjectModel3D1, ObjectModel3D2], [], PoseVis, \ ['point_size', 'color_0', 'color_1'], [2, 'red', 'blue'], \ [], [], [], PoseOut)
显示效果如下:
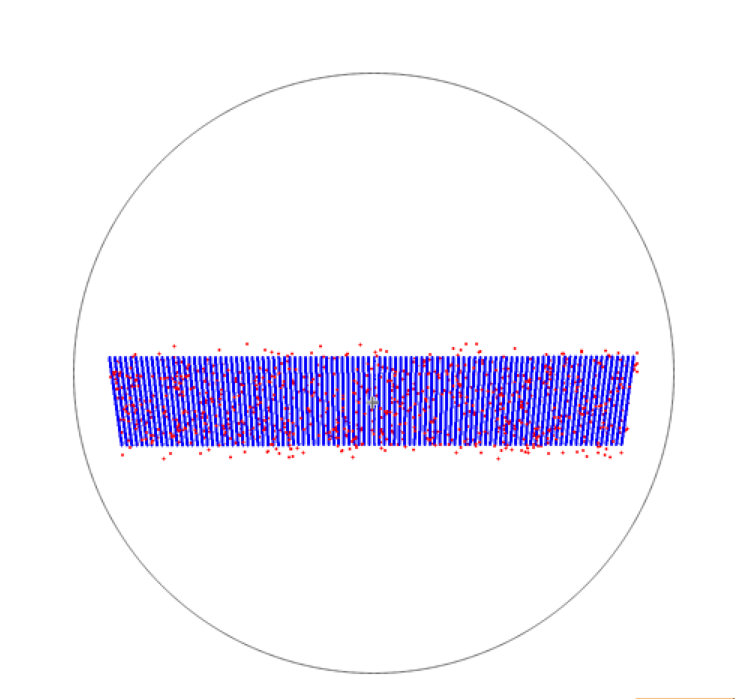
增加解三维直线方程:
dev_update_off() dev_close_window () Size := 500 dev_open_window (0, 0, Size, Size, 'white', WindowHandle) * 创建随机点 Z := rand(1000) * 100 X := rand(|Z|) * 6 Y := rand(|Z|) * 5 * 解三维直线方程 * x = k1 * z + b1 * y = k2 * z + b2 create_matrix (|X|, 2, 1.0, MatrixA) create_matrix (|X|, 1, Z, MatrixACol0) set_sub_matrix (MatrixA, MatrixACol0, 0, 0) create_matrix (|X|, 2, 1.0, MatrixB) create_matrix (|X|, 1, Y, MatrixBCol1) create_matrix (|X|, 1, X, MatrixBCol0) set_sub_matrix (MatrixB, MatrixBCol1, 0, 1) set_sub_matrix (MatrixB, MatrixBCol0, 0, 0) solve_matrix (MatrixA, 'general', 0, MatrixB, MatrixX) get_value_matrix (MatrixX, 0, 0, K1) get_value_matrix (MatrixX, 1, 0, B1) get_value_matrix (MatrixX, 0, 1, K2) get_value_matrix (MatrixX, 1, 1, B2) Line3dX := K1 * Z + B1 Line3dY := K2 * Z + B2 * 三维显示 dev_open_window (0, 0, Size, Size, 'white', WindowHandle) gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D1) gen_object_model_3d_from_points(Line3dX, Line3dY, Z, ObjectModel3D2) PoseVis := [-50, 0, 2000, 80, 0, 0, 0] visualize_object_model_3d(WindowHandle, [ObjectModel3D1, ObjectModel3D2], [], PoseVis, \ ['point_size', 'color_0', 'color_1'], [2, 'red', 'blue'], \ [], [], [], PoseOut)
三维直线拟合效果如下:
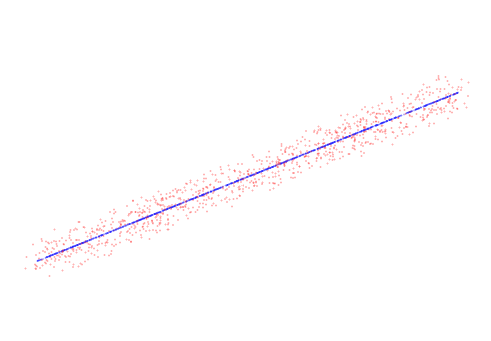





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话