一、格雷码的特点
格雷码是一种循环二进制码或者叫作反射二进制码。格雷码的特点是从一个数变为相邻的一个数时,只有一个数据位发生跳变,由于这种特点,就可以避免二进制编码计数组合电路中出现的亚稳态。格雷码常用于通信,FIFO或者RAM地址寻址计数器中。经常作为跨市终于处理的一种方法。切记在做跨时钟处理的时候要成对的出现。
二、二进制码转换为格雷码的方法
|
十进制 |
二进制 |
格雷码 |
十进制 |
二进制 |
格雷码 |
|
0 |
0000 |
0000 |
8 |
1000 |
1100 |
|
1 |
0001 |
0001 |
9 |
1001 |
1101 |
|
2 |
0010 |
0011 |
10 |
1010 |
1111 |
|
3 |
0011 |
0010 |
11 |
1011 |
1110 |
|
4 |
0100 |
0110 |
12 |
1100 |
1010 |
|
5 |
0101 |
0111 |
13 |
1101 |
1011 |
|
6 |
0110 |
0101 |
14 |
1110 |
1001 |
|
7 |
0111 |
0100 |
15 |
1111 |
1000 |
从自然的二进制码到GRAY码,就是GRAY的编码。具体方法是从二进制的最低位起(最右边的位数),依次起与左边的一位数进行异或运算,作为对应格雷码该位的值。而最高位保持不变。如下图所示:根据图示可以写出的代码:
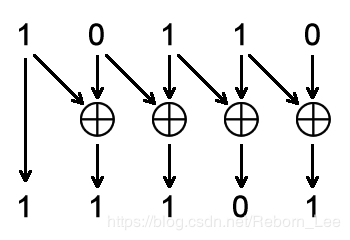
1 g[n] = b[n];//最高位不变 2 g[i] = b[i] xor b[i+1];//其中g,b 分别对应n位的格雷码和二进制码。 其实根据以上图示以及,表格中的对比,可以发现规律: 就是二进制码右移一位后与自身异或。所以可以描述数为:
assign gray = binary ^ binary(binary>>1);
三、格雷码转换为二进制码
具体的方法就是:从格雷码左边第二位(次高位),将每一位与其左边一位解码后的值进行异或,作为当前格雷码的值,而最左边一位(最高位)的解码结果就是它本身。如下图所示:
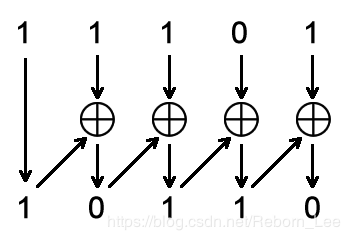
转换成逻辑代码就是:
b[n] = g[n] ;//最高位,保持不变 b[n] = g[i] xor b[i+1];//b和G都是n位的二进制码和格雷码。
转换成Verilog 语言实现:
1 // ********************************************************************************* 2 // Project Name : 3 // weixin : li15226499835 4 // Website : https://www.cnblogs.com/lgy-gdeu/ 5 // Create Time : 2020// 6 // File Name : .v 7 // Module Name : 8 // Abstract : 9 // editor : sublime text 3 10 // ********************************************************************************* 11 // Modification History: 12 // Date By Version Change Description 13 // ----------------------------------------------------------------------- 14 // 2020// Liguoyong 1.0 Original 15 // 16 // ********************************************************************************* 17 `timescale 1ns/1ns 18 module gray2bin #( 19 parameter N= 6 20 )( 21 //system signals 22 input wire [N-1:0] gray , 23 output wire [N-1:0] bin 24 25 ); 26 //============================================================================= 27 //**************************** Main Code ******************************* 28 //============================================================================= 29 assign bin[N-1] = gray[N-1];//最高位不发生改变 30 generate 31 genvar i; 32 for (i = N-2; i >=0; i = i - 1) 33 begin:gray_2_bin 34 assign bin[i] = bin[i+1] ^ gray[i]; 35 end 36 endgenerate 37 endmodule
在上述,实现中使用了generate for语句,现在改用平常的for语句,来实现。平常的For语句一定要出现在always 块中。
1 module gray_to_binary #(parameter N = 4 2 ) 3 ( 4 input [N-1:0] gray_value, 5 output [N-1:0] binary_value 6 ); 7 reg [N-1:0] binary_value; 8 integer i; 9 10 always@(*)begin 11 binary_value[N-1] = gray_value[N-1]; 12 for(i=0; i<=N-2; i=i+1)begin:U1 13 binary_value[i] = binary_value[i+1]^gray_value[i]; 14 end 15 end 16 endmodule
四、格雷码计数原理
格雷码计数器,采用三个模块进行设计,格雷码转二进制、加法器、二进制转格雷码。格雷码转二进制将格雷码转换为二进制,并将值输出用于加法器进行加法运算,然后将加法运算结果通过二进制转格雷码转换为格雷码,最后将格雷码进行输出,同时将结果输出到格雷码转二进制作为输入,形成一个计数功能。
1 module gray_counter #( 2 parameter data_width = 4 3 ) 4 ( 5 input wire clk, 6 input wire reset_n, 7 output wire [data_width-1:0] gray_out 8 ); 9 10 //格雷码转二进制 11 12 wire [data_width-1:0] bin_out; 13 14 gray_to_bin gray_to_bin_1( 15 16 .gray_in (gray_wire), 17 .bin_out (bin_out) 18 ); 19 20 //二进制加一 21 22 wire [data_width-1:0] bin_add_wire; 23 assign bin_add_wire = bin_out + 1'b1; 24 25 //二进制转格雷码 26 27 wire [data_width-1:0] gray_wire; 28 29 reg [data_width-1:0] gray_out; 30 31 bin_to_gray bin_to_gray_1( 32 33 .bin_in (bin_add_wire), 34 35 .gray_out (gray_wire) 36 37 ); 38 39 40 41 always @(posedge clk or negedge reset_n)begin 42 if(reset_n == 1'b0)begin 43 gray_out <= {data_width{1'b0}}; 44 end 45 else begin 46 gray_out <= gray_wire; 47 end 48 end 49 50 endmodule




