逻辑回归
逻辑回归是分类最简单的算法。
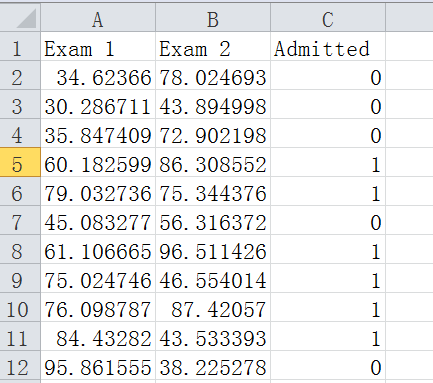
题目是有一个学校招生,考2门专业课。给出了100个样本,每一个样本包含2门课的成绩以及是否被录取。也就是LogiReg_data.csv数据。原始是txt格式,为了方便,人为的加上了表头。
1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 # 导入相关库,并重命名 5 pdData = pd.read_csv("LogiReg_data.csv") 6 #打开文件 7 positive = pdData[pdData['Admitted'] == 1] #将'Admitted'一列为1的行(样本)提取出来,放入positive 8 negative = pdData[pdData['Admitted'] == 0] #将'Admitted'一列为0的行(样本)提取出来,放入negative 9 fig, ax = plt.subplots(figsize=(10,5)) 10 #subplots固定用法 11 #subplots是matplotlib中的画子图像的函数, 12 #原型: 13 #plt.subplots( 14 # nrows=1, 15 # ncols=1, 16 # sharex=False, 17 # sharey=False, 18 # squeeze=True, 19 # subplot_kw=None, 20 # gridspec_kw=None, 21 # **fig_kw, 22 #) 23 #nrows,ncols控制几个子图,例如:nrows=1,ncols=2就是2个子图,左一个右一个。sharex、sharey控制 24 #是否共享x、y轴。返回值是两个,一个是fig,图像,一个是axes。figsize是图片大小。 25 ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o', label='Admitted') 26 ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x', label='Not Admitted') 27 #scatter可以用来画散点图,里边参数positive['Exam 1'], positive['Exam 2']分别是x轴和y轴是什么。“c”是可选颜色 28 #“marker”是可选点的形状,具体可以百度。s是size,为点的大小,label是图中'o'的点是'Admitted','x'是'Not Admitted' 29 ax.legend() 30 #ax.legend控制图例的参数,例如大小、位置、标题等等。https://blog.csdn.net/qq_35240640/article/details/89478439?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~all~first_rank_v2~rank_v25-2-89478439.nonecase 31 ax.set_xlabel('Exam 1 Score') 32 ax.set_ylabel('Exam 2 Score') 33 #set_ylabel是x轴和y轴的名称叫什么。用plt.xlabel和plt.ylabel也可以。 34 35 def sigmoid(z): 36 return 1 / (1 + np.exp(-z)) 37 #sigmoid 函数,用来映射成【0,1】的一个概率值 38 39 nums = np.arange(-10, 10, step=1) #np.arange构造一个【-10,10】的一个ndarray,步长为1.(10,-9,-8,-7…………,7,8,9,10) 40 fig, ax = plt.subplots(figsize=(12,4)) 41 ax.plot(nums, sigmoid(nums), 'r') #ax.plot画出sigmoid函数。其中sigmoid(0)=0.5 42 print(type(nums)) #发现nums就是一个ndarray。 43 44 def model(X, theta): 45 return sigmoid(np.dot(X, theta.T)) #np.dot 计算点积,需要注意的是,点积计算时,要求第一个参数的列数要和第二个参数的行数一样才可以。最后的返回值也是一个矩阵,列数为1 46 47 pdData.insert(0, 'Ones', 1,allow_duplicates=True) #在第一列数据前增加新的一列,变为0、1、2、3列 48 orig_data = pdData.iloc[:,:].values #将dataframe转成numpy.array。 49 cols = orig_data.shape[1] #计算出二位数组有几列,也可以写成cols=len(orig_data[0]) 50 X = orig_data[:,0:cols-1] #将前3列0、1、2列赋值给x 51 y = orig_data[:,cols-1:cols] #将最后一列赋值给y 52 theta = np.zeros([1, 3]) #创建一个theta [[0. 0. 0.]] 这里写np.zeros((1,3))也可以 53 54 55 56 def cost(X, y, theta): #定义损失函数,损失函数可以评判估计值和实际值的误差 57 left = np.multiply(-y, np.log(model(X, theta))) #np.multiply是参数相乘、乘法。np.log计算数学的log,model返回值是计算sigmoid,结果(0,1) 58 right = np.multiply(1 - y, np.log(1 - model(X, theta))) 59 return np.sum(left - right) / (len(X)) #np.sum求和,计算总的损失,再除以样本数量,就是平均损失。 60 61 cost(X, y, theta) 62 63 def gradient(X, y, theta): #用来计算梯度下降方向的,这里需要先对损失函数求导,目的是计算出损失最小的位置,参考数学公式。 64 grad = np.zeros(theta.shape) #grad是一个二维数组,[[0. 0. 0.]] 65 error = (model(X, theta)- y).ravel() #把error转成一维数组,是为后边的和X第j列相乘做准备 66 for j in range(len(theta.ravel())): #theta本身是二维数组,但是通过theta.ravel() 将theta转成一维数组, len(theta.ravel()) 计算数组长度,在这里实际长度是3。 67 term = np.multiply(error, X[:,j]) #注意X是一个二维数组,所以采用X[:,j]选取所有行的第j列。 68 grad[0, j] = np.sum(term) / len(X) #grad是一个二维数组,[[0. 0. 0.]],theta有三个参数,所以要计算三个梯度的方向 69 return grad #grad是一个二维数组,[[0. 0. 0.]] 70 71 STOP_ITER = 0 72 STOP_COST = 1 73 STOP_GRAD = 2 74 #设定三种不同的停止策略 75 def stopCriterion(type, value, threshold): 76 if type == STOP_ITER: return value > threshold #设定迭代次数 77 elif type == STOP_COST: return abs(value[-1]-value[-2]) < threshold #给损失函数cost设定阈值 78 elif type == STOP_GRAD: return np.linalg.norm(value) < threshold #给梯度设定阈值 注意三种情况返回的都是bool值 79 80 import numpy.random 81 #洗牌,无法保证数据是具有随机性,通过np.random.shuffle函数打乱数据顺序,使数据具有随机性 82 def shuffleData(data): #函数的功能就是将X和y数据重新排列组合 83 np.random.shuffle(data) 84 cols = data.shape[1] #计算出二位数组有几列,也可以写成cols=len(orig_data[0]) 85 X = data[:, 0:cols-1] #重新选择X,但是和之前一样,还是第0、1、2列 86 y = data[:, cols-1:] #重新选择y,但是和之前一样,还是第3列 87 return X, y 88 89 90 import time 91 92 93 def descent(data, theta, batchSize, stopType, thresh, alpha): 94 # 梯度下降求解 95 96 init_time = time.time() # 显示计算时间 97 i = 0 # 迭代次数 迭代次数越多,损失函数越趋于0,看图像就可以 98 k = 0 # batch 选取的样本,当k=1时,一个样本计算一次,计算速度快,但不一定收敛,这是随机梯度下降; 99 # 但是慢当k=10时,10个样本计算一次,比较实用,这是小批量梯度下降;当k=样本数量时,计算所有样本,速度慢,但是容易找到最优解,这是批量梯度下降。 100 X, y = shuffleData(data) # 调用shuffleData函数,打乱数据 101 grad = np.zeros(theta.shape) # 初始化grad,grad是梯度 102 costs = [cost(X, y, theta)] # 初始化损失值,这里打算用appand,所以新生成的costs是二维数组。 103 # 以上是将变量初始化。 104 while True: # 死循环,碰到break停止 105 grad = gradient(X[k:k + batchSize], y[k:k + batchSize], 106 theta) # X和y是二维数组X[k:k+batchSize],意思是第k行到第k+batchSize行,y同理 107 k += batchSize # 取batch数量个数据 108 if k >= n: # n会在后边赋值,这个n代表如果计算的样本数量超出了原来的样本数量,就重新洗牌,重新计算参数 109 k = 0 110 X, y = shuffleData(data) # 重新洗牌 111 theta = theta - alpha * grad # 参数更新,可以参考数学部分 112 costs.append(cost(X, y, theta)) # 计算新的损失 113 i += 1 114 115 if stopType == STOP_ITER: 116 value = i 117 elif stopType == STOP_COST: 118 value = costs 119 elif stopType == STOP_GRAD: 120 value = grad 121 if stopCriterion(stopType, value, thresh): break 122 123 return theta, i - 1, costs, grad, time.time() - init_time 124 125 def runExpe(data, theta, batchSize, stopType, thresh, alpha): 126 #import pdb; pdb.set_trace(); 127 theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha) 128 #以下都是为图的标题做准备的 129 name = "Original" if (data[:,1]>2).sum() > 1 else "Scaled" 130 name += " data - learning rate: {} - ".format(alpha) 131 if batchSize==n: strDescType = "Gradient" 132 elif batchSize==1: strDescType = "Stochastic" 133 else: strDescType = "Mini-batch ({})".format(batchSize) 134 name += strDescType + " descent - Stop: " 135 if stopType == STOP_ITER: strStop = "{} iterations".format(thresh) 136 elif stopType == STOP_COST: strStop = "costs change < {}".format(thresh) 137 else: strStop = "gradient norm < {}".format(thresh) 138 name += strStop 139 print ("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format( 140 name, theta, iter, costs[-1], dur)) 141 #以上都是为图的标题做准备的 142 fig, ax = plt.subplots(figsize=(12,4)) 143 ax.plot(np.arange(len(costs)), costs, 'r') 144 ax.set_xlabel('Iterations') 145 ax.set_ylabel('Cost') 146 ax.set_title(name.upper() + ' - Error vs. Iteration') 147 plt.show() 148 return theta 149 n=100 150 runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.000001) #1.1次 151 #一次选取整个样本,采用控制迭代次数的方式,5000次,Last cost: 0.63,time=1.69s 152 runExpe(orig_data, theta, n, STOP_ITER, thresh=50000, alpha=0.000001) #1.2次 153 #一次选取整个样本,采用控制迭代次数的方式,5000次,Last cost: 0.63,time=17.30s 154 runExpe(orig_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001) #1.3次 155 #一次选取整个样本,采用控制迭代次数的方式,5000次,Last cost: 0.61,time=1.69s 156 #1.2和1.1次相比,迭代次数*10,时间也大约*10,但是损失值并没有降低,所以这种情况下增加迭代次数并没有用。 157 #1.1和1.3相比,迭代次数不变,学习率降低,但是cost并没有降低很多,一般的cost取0.001比较合适 158 runExpe(orig_data, theta, n, STOP_COST, thresh=0.000001, alpha=0.001) #2次 159 #一次选取整个样本,采用控制cost方式,Last cost: 0.38,time: 38.37s,需要迭代11000次左右 160 #通过增大或者减小cost的值很容易发现,cost越小,迭代次数越多,消耗时间越多;cost增大则相反。 161 runExpe(orig_data, theta, 100, STOP_GRAD, thresh=0.02, alpha=0.001) # 3.1次 162 #一次选取整个样本,采用控制grad梯度下降速度方式,Last cost: 0.31,time: 78.83s,需要迭代220000次左右 163 runExpe(orig_data, theta, 100, STOP_GRAD, thresh=0.05, alpha=0.001) # 3.2次 164 #一次选取整个样本,采用控制grad梯度下降速度方式,Last cost: 0.49,time: 14.96s,需要迭代40000次左右 165 #3.2和3.1对比,增大grad,发现迭代次数降低,cost升高。实际上grad为0时为最理想值,但是耗时非常大。 166 runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha=0.001) #4次 167 #一次选取1个样本,采用控制迭代次数方式,图像不稳定,说明1个样本下模型不收敛,也就是结果不趋于0 168 #即使增加迭代次数也没用,减小学习率alpha也没用,图像始终不稳定。 169 runExpe(orig_data, theta, 16, STOP_ITER, thresh=15000, alpha=0.001) #5次 170 #一次选取16个样本,采用控制迭代次数方式,图像仍然不稳定,所以在控制迭代次数方式这里,问题出在了数据 171 #需要对数据进行标准化 172 173 #以下是数据进行标准化 174 from sklearn import preprocessing as pp 175 scaled_data = orig_data.copy() 176 scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3]) 177 #以上是数据进行标准化 178 runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha=0.001) #6次 179 #一次选取整个样本,采用控制迭代次数的方式,5000次,Last cost: 0.38,time:1.92s 180 #6次和1.1次相比,是数据标准化之后的结果,发现时间上没有太大改善(因为迭代次数没有变),但是cost下降了很多 181 #所以数据预处理很重要,要先进行标准化,去量纲,变为纯数 182 runExpe(scaled_data, theta, n, STOP_GRAD, thresh=0.02, alpha=0.001) #7次 183 #一次选取整个样本,采用控制grad梯度下降速度方式,迭代次数不到60000次,Last cost: 0.22 - time: 22.24s 184 #7次和3.1相比,是数据标准化之后的结果,迭代次数减小,时间减小,cost降到了0.22 185 runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.02, alpha=0.001) #8次 186 #一次选取1个样本,采用控制grad梯度下降速度方式,迭代次数15000次左右,cost: 0.28,time:1.95s 187 #8次和7次相比,样本数为1,整体迭代次数缩减了很多,时间缩减了很多 188 189 theta = runExpe(scaled_data, theta, 1, STOP_GRAD, thresh=0.002/5, alpha=0.001) #9次 190 #一次选取1个样本,采用控制grad梯度下降速度方式,70000多次,cost降到了0.22 - time: 8.78s 191 runExpe(scaled_data, theta, 16, STOP_GRAD, thresh=0.002*2, alpha=0.001) #10次 192 #一次选取16个样本,采用控制grad梯度下降速度方式,6000多次,cost降到了0.21 - time: 1.19s 193 #需要注意的是10次和9次比,虽然看起来只是变了计算一次的样本数量,但是10的theta初试值并不是0, 194 #而是用的9次的计算结果,也就是说初始值是经过训练之后的值,所以迭代次数大幅下降。 195 196 def predict(X, theta): #函数功能是用原始数据验证模型的准确性 197 #return [1 if x >= 0.5 else 0 for x in model(X, theta)] #这是原博主写的,但是不太好理解,但是习惯矩阵运算很重要 198 a = [] 199 for i in model(X, theta): 200 if i>=0.5: 201 a.append(1) 202 else: 203 a.append(0) 204 return a #函数的返回值是一个list,是每一个样本是否被录取的结果[1, 0, 1, 1, 0,…………, 1, 1, 1, 0] 205 206 scaled_X = scaled_data[:, :3] #选取前三列数据 207 y = scaled_data[:, 3] #选取最后一列数据 208 predictions = predict(scaled_X, theta) #predictions是预测值 209 correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)] 210 #correct是一个list,如果真实值和预测值相等,该位置写1,否则写0.这里也可以用for循环实现。 211 #zip函数是将(predictions, y)组合成一个可迭代对象,不然for循环无法实现。 212 accuracy = (sum(map(int, correct)) % len(correct)) #map是将correct转成int型list(猜的),可以不用map,分开计算也可以 213 print ('accuracy = {0}%'.format(accuracy)) #计算概率,需要注意的是,这里是整数除以整数。format很简单,百度就可以
数学公式:
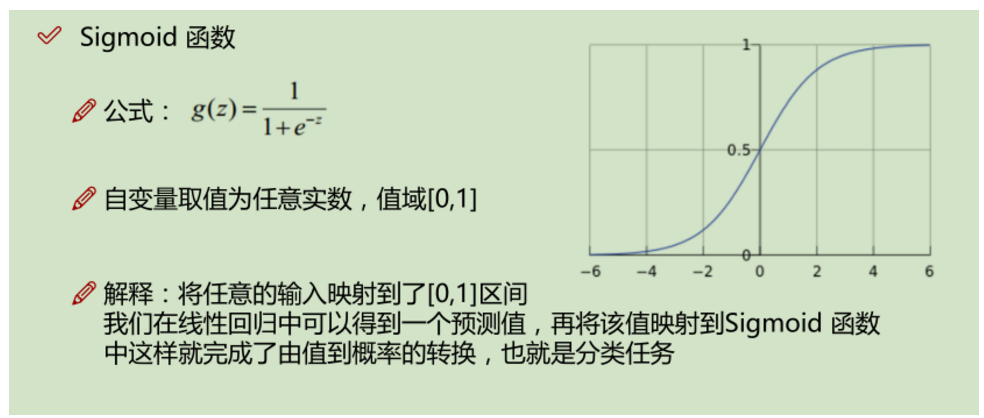


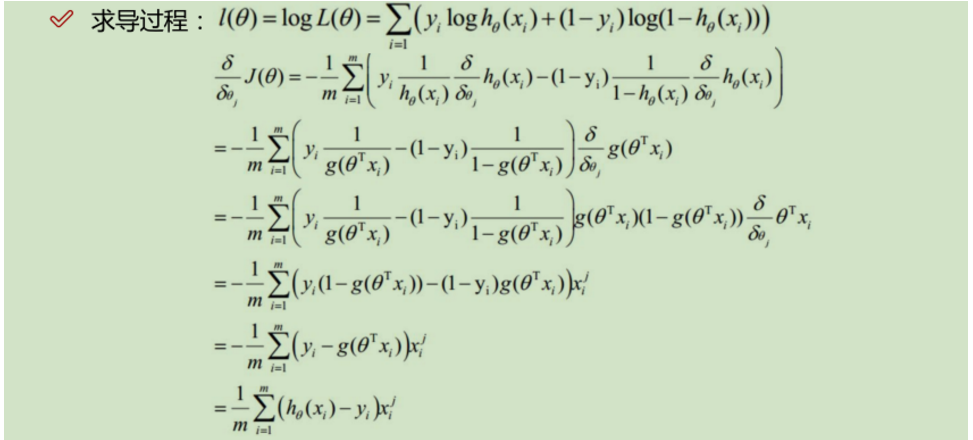

以上是根据唐宇迪视频,以及某博客https://www.cnblogs.com/douzujun/p/8370993.html所写
代码是基于python 3.7,没有任何问题。



