杂题乱做笔记
P2587 [ZJOI2008]泡泡堂
简单小清新题。但是甚至先写了一发假的贪心
对于最大值，把 \(a\) 排序，把所有 \(b\) 丢进一个 multiset 。
首先最大化 \(2\) 贡献的次数，从小到大对于每个 \(a\) ，在 \(b\) 中找一个他能打败的最强的打败即可。
然后最大化 \(1\) 贡献的次数，再用一个 map 存一下每个数出现的次数直接匹配就好了。
最小值直接 swap(a,b),writeln(2*n-solve()); 即可。
复杂度 \(O(n\log n)\)。
CF1474E What Is It? *2500
一开始猜了个 \((n-1)^2+(n-2)^2+(n-3)^2+...\) 发现不对，然后又猜了个 \((n-1)^2+2\times(n-2)^2+2\times(n-4)^2+...\) 又错了。看了一眼 CF 上的数据，发现很有规律，然后就会了。
首先思考答案的上界，那么显然是让每个位置向离其最远的位置交换，那么对于 \(1 \sim \lfloor \dfrac n2 \rfloor\) 向 \(n\) 连显然最优，对于 \(\lfloor \dfrac n2 \rfloor +1 \sim n\) ，向 \(1\) 连显然最优，所以答案上界为 \((n-1)^2+2\times(n-2)^2+2\times(n-3)^2+...\)。
所以 \(\{\lfloor \dfrac n2 \rfloor +1 \sim n-1\}\) 依次与 \(1\) 交换（其实这样本质上形成了一个置换环），\(\{1 \sim \lfloor \dfrac n2 \rfloor\}\) 依次与 \(n\) 交换即可。
构造显然是可以做到的，即对于一个初始的 identity permutation，倒着把操作做一遍就好了。
复杂度 \(O(n)\)。
总结： 构造题思考理论上界，这样就为构造找到了方向与证明。
CF1455F String and Operations *2800
容易发现原本在第 \(i\) 个位置上的字符只能在 \(i-1\) 或 \(i\) 上，那么设 \(f_{i,0/1}\) 表示第 \(i\) 次操作后第 \(i+1\) 个字符是否在 \(i+1\) 的位置上，然后直接转移即可。具体转移有些细节，见代码。
复杂度 \(O(n)\)。
总结： 可以思考一下发现不可能将 \(0/1\) 那一维压掉，因为当前的局部最优不一定满足全局最优。所以这个 dp 的本质便是通过多设状态来使得所有策略都被考虑到，当某些转移不合法或最优解不能被考虑到时可以考虑这种做法。
CF1381C Mastermind *2500
首先发现值域是 \(n+1\) ，很自然地发现有一个数没有出现过，这样就解决了 \(n-y\) 个没出现过的数的问题。
那 \(x\) 个数目前不好确定，不妨先考虑如何让这之外的 \(n-x\) 个数对应位置上全部不相同，由此得到策略之后再考虑那 \(x\) 个。
我们现在想让同样的数在不同的位置上，想到一种策略：先将 \(a\) 按出现个数从小到大排序（求出答案之后映射回去即可），然后在 \(b\) 中将出现次数最多的放在最前面，然后其他数按照在 \(a\) 中的顺序一次填即可。
例如序列 \(a=[ 1,1,2,3,2,2,4,4,4]\)，将 \(a\) 重排后得到 \([3,1,1,2,2,2,4,4,4]\)，所以 \(b=[4,4,4,3,1,1,2,2,2]\) ，容易发现这种策略下只有出现次数最多的数可能有交，那么这就确定了 \(x\) 的策略：让剩下的 \(n-x\) 个数中出现次数最多的数出现次数最少（使得出现次数最多的数尽量无交）。
具体来说，维护一个按出现次数排序的大根堆，对于前 \(x\) 个数，每次取出堆顶即可。
但是即使这样，记剩下的 \(n-x\) 个数中出现次数最多的数有 \(k\) 个，那么可能出现 \(n-x-k<k\) 的情况，那么这样子就可以利用 \(n-y\) 个没有出现过的数来隔开这些数，如果最优情况下仍隔不开，那么无解。
复杂度 \(O(n \log n)\)，瓶颈在于排序。
CF1601D Difficult Mountain *2700
发现不是很好找到一种贪心顺序，那么考虑 dp，也就是说需要确定一个顺序。
发现当 \(a_i \leq s_j\) 且 \(s_i \leq a_j\)，\(i\) 必定在 \(j\) 的前面选择更优。然而这种偏序不能直接排序，那么将其加强到其的一个必要条件：\(a_is_i \leq a_js_j\) ，用这个排序即可。
排完序之后直接线段树优化 dp 即可，复杂度 \(O(n\log n)\)。
事实上有直接按 \(\max\{a_i,s_i\}\) 排序然后直接贪心的高妙做法，待填。
CF1452F Divide Powers *2900
可以发现有 2 种性价比不同的操作：
- \(2^i \to 2\times2^{i-1}\) ，做 \(t\) 次收益为 \(t\) 。
- \(2^y \to 2^{y-x} \times 2^{x}\)，做 \(2^{y-x}-1\) 次收益为 \(2^{y-x}\) 。
那么从小到大枚举 \(y \ (y >x)\) ，在 \(k\geq 2^{y-x}\) 的情况下（每次操作 \(k \gets k-2^{y-x}\)）显然每次能做第二种就做第二种，直到 \(k < 2^{y-x}\) 。
接下来的决策有：将一个 \(2^{y}\) 拆成一些 \(2^x\) ，但不全拆完（比如 \(x=1,y=3,8 \to 4+2+2\)），以及用第一种操作。
但是我们并不知道“不全拆完”到底怎么拆，所以考虑枚举。枚举一个 \(x<z\leq y\) ，同时维护一个 \(cnt\) 表示将 \(k \leq x\) 的全部拆掉能拆多少次，然后在不超过 \(k\) 的情况下每次把一个 \(2^z \to 2^{z-1}+2^{z-x}\times2^x\)，更新答案即可，复杂度 \(O(qn)\)。
P6943 [ICPC2018 WF]Conquer The World
一种显然错误的贪心是，枚举每个点作为 \(lca\)，然后直接贪心地匹配子树内的点对。
考虑反悔，对于两个点 \(x,y\) ，他们在 \(lca=a\) 处匹配的代价是 \(dep_x+dep_y-2dep_a\) ，如果 \(x\) 在之后的 \(lca=b\) 与 \(z\) 匹配更优，此时的代价是 \(dep_x+dep_z-2dep_b\)，那么两次的差值是 \(dep_z-2dep_b-(dep_y-2dep_a)\)。那么初始时将每个点的需求点 \(dep\) 存入一个小根堆，供给点 \(dep\) 存入另一个小根堆，然后 \(dfs\) 的时候可并堆合并即可，合并之后将 \(2dep_a-dep_x,2dep_a-dep_y\) 分别存回对应的堆即可。
注意到需要满足所有需求点的条件，那么给每个需求点的代价 \(w \gets w-\inf\) 即可，复杂度 \(O(n \log n)\)。
BZOJ2264 Free Goodies
假定 Jan 先手。
首先按 \(a\) 为第一关键字从大到小，\(b\) 为第二关键字从小到大排序，那么 Petra 每次取的一定是没取过的最左边的。
之后就是经典结论：对于任意前 \(i\) 个元素，Jan 最多取 \(\lceil \dfrac i2 \rceil\) 个，设 \(f_{i,j}\) 为前 \(i\) 个 Jan 取了 \(j\) 个的最大价值，\(g_{i,j}\) 表示这种策略下 Petra 的最大价值，直接转移即可。对于 Petra 先手，让他拿走第一个，然后转化成 Jan 先手继续做即可。
复杂度 \(O(n^2)\) 。
Bonus： \(n\leq 1 \times 10^6\)。
把 Jan 取的看作 \(-1\)，Petra 取的看作 \(+1\)。初始全为 \(+1\) ，那么每次操作相当于把一个 \(+1\) 变成 \(-1\) 且要求没有 \(< -1\)的地方，使用线段树维护每个位置的前缀和，每次二分找出最靠右的 \(\leq1\) （若没有则为 \(0\)）的位置 \(p\) ，在 \([p+1,n]\) 中查找最优解，在这之后区间 \(-2\) 即可，复杂度 \(O(n \log n)\)。
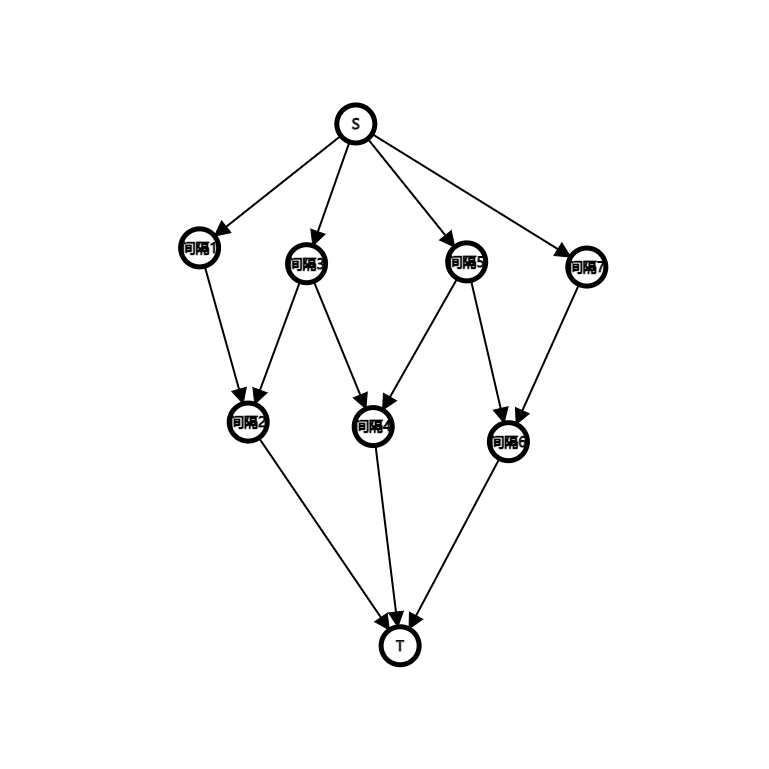
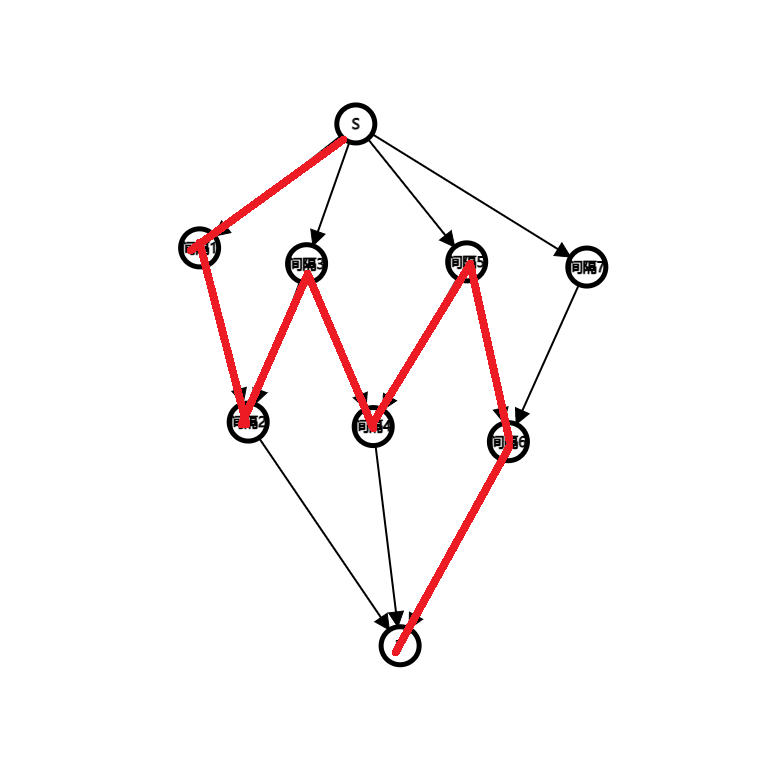
P3620 [APIO/CTSC2007] 数据备份
问题显然可以转化成在一个长度为 \(n-1\) 的差分数组里，选出 \(k\) 个不相邻的数的最小代价。
考虑模拟费用流。
建图，相当于两个间隔之间最多可以贡献一个点的代价，那么源点向每个奇数间隔连容量为 \(1\)，费用为 \(0\) 的边，每个奇数间隔向相邻的间隔连容量为 \(1\) ，费用为其代价 \(a_i\) 的边，每个偶数间隔再向汇点连容量为 \(1\) ，费用为 \(0\) 的边即可，这样流一条边就相当于填了这两个间隔中间的那一个点。
流量为 \(k\) ，跑最小费用最大流即可（其中间隔 \(1\) 指的是点 \(1\) 前面的间隔，间隔 \(7\) 指的是点 \(6\) 后面的间隔）。
考虑一次增广，比如长成这个样子（经过了一些前向边和一些反向边）：
那么相当于把 \(2,4\) 变成了 \(1,3,5\) 。
直观一点地，那么每次操作就是把 [ 不选 ... 不选 ] [不选，选，不选，选，不选] [ 不选 ... 不选 ] 合并成 \(1\) 个两端依然都是不选的区间。
所以考虑维护一个堆，每个元素代表其的区间翻转所需的代价，同时维护一个链表用来查前驱后继。
每次从堆里面取出一个点的时候，把他的前驱后继都删掉，设前驱代价为 \(x\) ，后继代价为 \(y\) ，当前代价为 \(z\) ，那么让答案加上 \(z\) 并且往堆里插入一个 \(x+y-z\) 即可。
复杂度 \(O(n \log n)\) 。
P4609 [FJOI2016]建筑师
发现把相邻两个最值之间的数归给前一个，这样分成了若干个集合，且要求最大的数排在最前面，而这与轮换数等价。
所以相当于把 \(1 \sim n-1\) 这些数分成若干个轮换，再把轮换放在 \(n\) 的两边。
所以答案是 \(\displaystyle {n-1 \brack a+b-2}{a+b-2 \choose a-1}\)。
P5419 [CTSC2016]单调上升序列
出题人把做法写题面里，谢谢出题人！！1
出题人在题面里告诉了我们结论：考虑初始如果在每个点上放一个棋子，对于一个图，从小到大枚举每条边，然后交换这两个棋子，最后会发现每个棋子都走出了一个上升路径，并且一共有 \(n(n-1)\) 条边，且有 \(n\) 条路径，于是答案下界为 \(n-1\)。
考虑构造，相当于把 \(\dfrac{n(n-1)}{2}\) 分成 \(n-1\) 组匹配，然后一组一组地给边从小到大标号，容易发现这样子只能从前面的匹配走到后面的匹配，那么最长的路径不会超过 \(n-1\)。
这样就转化成了一个对称拉丁方：首先做一个 \(n-1\) 的拉丁方出来：令 \(a_{i,j}=(i+j)\bmod (n-1)\)。
然后让所有的 \(a_{i,i}=0\)，把原来的 \(a_{i,i}\) 移到 \(a_{n,i}\) 与 \(a_{i,n}\) 即可。
CF1493E Enormous XOR *2600
考虑怎么快速计算 $ \oplus_{i=x}^y i$，发现一个性质：当 \(i\) 为偶数时 \(i \oplus (i+1)=1\)，这样可以通过左右端点的奇偶性以及区间长度模 \(4\) 的值得到异或的结果。
首先若 \(l,r\) 首位不同那么答案显然是 \(111\cdots111(2^{n} \oplus 2^{n}-1)\)。
如果首位相同，那么答案至少是 \(r\)。
然后你发现 \([x,y]\) 的异或和只可能有 \(6\) 种结果：\(x,x \oplus 1,y,y \oplus 1,x\oplus y,x\oplus y \oplus 1\)，前两种肯定不优，后两种最高位抵消了，所以也不优，所以现在只关心能不能取到 \(y \oplus 1\)。
简单分析可以得到当且仅当区间长度 \(\geq 3\) 并且 \(2 \mid r\) 的时候答案是 \(r+1\)，否则是 \(r\)。
CF1463F Max Correct Set *3100
结论：答案一定是以 \(x+y\) 为周期的。
证明：令 \(p=x+y,n=kp+r\)。
将 \([1,n]\) 划分为 \(2k+1\) 个区间，其中奇数的长度为 \(r\) ，偶数的长度为 \(p-r\)，设第 \(i\) 个区间里选了 \(v_i\) 个。
然后设 \(b_i\) 为对于最优解，把第 \(i\) 个区间复制到与他同奇偶的所有区间上答案增加了多少。
即若最优解答案为 \(x\)，其中奇数个区间的和为 \(y\)，偶数个区间的和为 \(z\)。
那么 \(y=\sum\limits_{j=0}^{k}v_{2j+1},z=\sum\limits_{j=1}^{k}v_{2j}\)，\(b_i=(k+1)v_i-y,2 \not\mid i\)，\(b_i=kv_i-z,2 \mid i\)。
那么有 \(\sum\limits_{j=0}^{k}b_{2j+1}=(k+1)\sum\limits_{j=0}^{k} v_{2j+1}-(k+1)y=0\)，同理可得 \(\sum\limits_{j=1}^{k}b_{2j}=0,\sum\limits_{i=0}^{2k+1} b_i=0\)。
若把任意一个 \(b_i,b_{i+1}\) 复制给整个区间都不优，即 \(b_i+b_{i+1} <0\)，由 \(\sum b_i=0\) 可知对所有 \(2 \not \mid i,b_i>0\)。
这与 \(\sum\limits_{j=0}^{k}b_{2j+1}=0\) 矛盾，所以答案呈周期性。
所以只需 dp 出 \([1,x+y]\) 的最优解即可，直接状压，只需保留最高的 \(\max(x,y)\) 位即可，复杂度 \(O((x+y)2^{\max(x,y)})\)。
CF1372E Omkar and Last Floor *2900
首先 \(y=x^2\) 是凸的，并且 \((x+y)^2 > x^2+y^2\)，所以尽量把 \(1\) 放在一起一定是最优的。
然后有一个显然的贪心：选一列放尽量多的数，然后往两边递归下去。
这显然是一个区间 dp 的形式，直接做就好了。
具体地，设 \(f_{i,j}\) 为只考虑被 \([i,j]\) 完全包含的区间的最大答案。
转移：\(f_{i,j}=\max\limits_{k=i}^j \{ f_{i,k-1}+f_{k+1,j}+t^2\}\)，其中 \(t\) 是被区间 \([i,j]\) 完全包含的中包含 \(k\) 的区间个数。
复杂度 \(O(n^3)\)。
P7914 [CSP-S 2021] 括号序列
去年没做出来，我考场上大概在睡觉。
一脸区间 dp，然后设 \(f_{i,j}\) 为 \([i,j]\) 的所有方案数，按照题目说的转移就好了。
然后发现第二个样例寄了，怎么会是呢？
你就发现 \(ASBSC\) 这种串会算两次，\(ABC\) 这种串也会算两次，还有 \(ASBC\) 之类的。
所以再设一个数组 \(g_{i,j}\) 表示 \(i,j\) 是一对匹配的括号的时候的方案数，然后 \(AB,ASB\) 的转移强制令左半边区间从 \(g\) 转移而来即可，由于题目条件的优秀性质（除了这两类其他最外面都要包一对括号），这样做就是对的。其中 \(ASB\) 的转移可以加一个前缀和优化。
复杂度 \(O(n^3)\)。
P7915 [CSP-S 2021] 回文
和上一题加起来花了 \(2h\) 左右想+写+调，结果去年花了 \(3h+\) 这两题一共拿了 \(47pts\)，我去年大概真的在睡觉。希望今年赛场上状态正常一些。
首先发现只要知道了第一个取啥，就知道了最后一个取啥，这样这个序列就被劈成了两边。
例如 \(4,1,2,4,5,3,1,2,3,5\) ，如果第一个取左边的，那么会劈成 \([1,2]\) 和 \([5,3,1,2,3]\) 两半。
然后思考一下有什么策略，一种想法是每次贪心地取左边的，然后判合法性，但是发现合法性不太好判。
然后想到能不能把这个回文串两边同时往中间做，发现是可以的！每次相当于在左边的开头或者右边的结尾取一个放在序列的开头，在左边的结尾或者右边的开头取一个放在序列的结尾，且要求这两个数相同，直接贪心做就完事了。
复杂度 \(O(n)\)。
UVA11181 条件概率 Probability|Given
算是板子题吧，学习一下条件概率。
定义 \(P(A)\) 为事件 \(A\) 发生的概率， \(P(AB)\) 为事件 \(A,B\) 同时发生的概率，\(P(A \mid B)\) 为在 \(B\) 发生的条件下 \(A\) 发生的概率。
那么显然有 \(P(AB)=P(A)P(B\mid A)\)，所以可以定义条件概率为 \(P(B \mid A)=\dfrac {P(AB)}{P(A)}\)，感觉一般肯定是用条件概率算 \(P(AB)\) ，但是也存在 \(P(AB)\) 好算的情况，用它来反推条件概率。
这道题设时间 \(A_i\) 表示第 \(i\) 个人去买了东西，\(B\) 表示有 \(r\) 个人买了东西，那么就是要求所有的 \(\dfrac{P(AB)}{P(B)}\)，上面相当于钦定第 \(i\) 个人买了，然后剩下 \(n-1\) 个人里面有 \(r-1\) 个人买了，可以跟下面一样求出来，直接 dp，复杂度 \(O(n^2r)\)。
CF123E Maze
记 \(u\) 作为起点的概率为 \(q_u\) ，作为终点的概率为 \(p_u\)。
题目给的代码可以看作一个从某个点开始，以它为根 dfs 到终点的步数，这启发我们直接考虑以每个点为根，到达所有可能终点的期望步数之和。
首先可以观察出几个性质：
假设当前的根为 \(x\)，终点是 \(y\)，那么从 \(x\) 开始走，考虑其中的一步。
- 如果这一步进入了与 \(y\) 所在子树不同的一个子树，一定会把这个子树内的所有点遍历完才出来。假设进入了一个以 \(z\) 为根的子树，大小为 \(sz_z\)，那么这个子树内的边数就是 \(sz_z-1\)，所需步数即为 \(2(sz_z-1)+2=2sz_z\)。
- 如果走进了了 \(y\) 所在的子树，那么就不会再出来。
对于一个点，记 \(y\) 所在的子树的根为 \(u\)。
由上面的性质可以知道，对于一个点，如果一个它的一个儿子 \(v \not=u\) 在 \(u\) 之前被访问，那么答案就会加上 \(sz_v\)。而 \(v\) 在 \(u\) 之前被访问的概率相当于给这个点的儿子随机一个排列，其中 \(v\) 在 \(u\) 之前的概率。考虑对于每种 \(v\) 在 \(u\) 之前的排列，swap(u,v) 之后就会得到一个 \(u\) 在 \(v\) 之前的排列，所以概率是 \(\dfrac 12\)。
接下来设 \(S\) 为 \((x,fa_y)\) 这条路径上的点分叉出去的点集的并，那么 \(x\) 走到 \(y\) 的期望就是 \(\sum\limits_{u \in S} \dfrac{2sz_u}{2}\)，对答案的贡献就是 \(q_xp_y\sum\limits_{u \in S}sz_u\)。
接下来就考虑对于每个根 \(x\) 求出 \(p_y\sum\limits_{u \in S}sz_u\)，先考虑以 \(1\) 为根。
设 \(f_u\) 表示以 \(u\) 为起点，到达 \(u\) 子树的的所有可能终点的期望步数之和，设 \(s=\sum\limits_{v \in son_u} sz_v=sz_u-1\)，\(t_u=\sum\limits_{v\in Subtree_u} p_u\)。
那么转移就是 \(f_u=\sum\limits_{v \in son_u} (s-sz_v+1)t_v+f_v\)。
换根也非常容易，首先对于每个点的 \(\sum t_v\) 可以提前维护出来，这样子 \(s\) 的变化导致的答案增量也很容易算出，具体的转移可以见代码。
复杂度 \(O(n)\)。
CF1081E Missing Numbers *1900
大水题，考虑把 \(a_{2k-1}\) 和 \(a_{2k}\) 分成一组，那么现在相当于这一组的开头大于上一组的结尾，且要求这一组的差分为完全平方数。
所以直接暴力分解当前数，为了让后面的选择更多，贪心地取 \(a_{2k}\) 最小的那一组即可，复杂度 \(O(n\sqrt n)\)。
P8496 [NOI2022] 众数
联想到 CF 的那道 Choosing Ads，所以可以考虑摩尔投票。
要支持删除，所以对每个队列维护一个权值线段树，然后叶子节点记录出现次数，合并的时候直接摩尔投票就好了。
操作 \(1,2\)，可以用一个链表配合线段树修改，操作 \(4\) 直接线段树合并+链表合并即可。
操作 \(3\) 直接查询这几个队列的根节点，摩尔投票合并，然后再在这几个线段树上查询出现次数之和来 check 即可。
复杂度 \(O(n \log n)\)。
P4684 [IOI2008] \(sa \sim ka \sim na \sim\)
容易得到一个关键性质：同种颜色中的长度较大鱼的可能决策一定包含那些小于它的鱼，所以统计答案的时候可以只考虑每种颜色的最长鱼。
一种想法是，将颜色按最长鱼的长度排序，然后对于每条最长鱼限制其只能选取前面的鱼。这样会算漏一种情况：当前的鱼可以吃掉后面的一些鱼。
思考这种情况为什么不会被后面的考虑到，显然是因为这条鱼在当前颜色的鱼中选择的鱼更多，所以可以考虑补上这种决策。
称只考虑之前的鱼的决策为 \(A\) 类决策，考虑吃掉后面的鱼的决策为 \(B\) 类决策，要求不重不漏。
考虑调整当前决策使得不与后面冲突（而不是后面考虑前面有哪些算过的）那么如果要得到当前可行的 \(B\) 类决策，自然要求其不与后面所有的 \(A,B\) 类决策重合。
也就是说对于在当前颜色能吃掉的鱼的个数 \(>\) 当前最长鱼能吃掉当前颜色的鱼的个数的那些后面的颜色，显然不能选，其他能选的可以任意选。由于单调性，这样的颜色形成的是一个区间，这样就很好维护了。具体地，将所有鱼按长度排序，依次考虑所有的最长鱼，把可行的新决策加入即可（因为单调性）。
由于区间乘积任意模数下不支持求逆，所以维护一棵线段树来查乘积，就做完了。
可以作进一步的思考：为什么不使用 ”后面考虑前面有哪些算过的“ 的这种计算方法呢？事实上，这道题的单调性在这种算法上体现为每个位置的决策数量都减少，而不是最终做法中的可决策位置的减少，这显然是很难做到一个位置一个位置修改的。所以可以归纳出一个东西：对于当前决策避免与后面决策算重的方法，会使得可行的位置更少；对于后面避免与前面位置算重的方法，每个位置上可行的数量会变少。
CF1139D Steps to One *2300
-
Method 1：牛逼的题解区的做法
首先有一个经典结论：\(E(x)=\sum\limits_{i \geq 1} P(x\ge i)=1+\sum\limits_{i\geq 1}P(x>i)\)。
所以设 \(x\) 为最终序列长度，那么：
\(P(x>i) =P(\gcd\limits_{j=1}^i a_j >1) = 1- P(\gcd\limits_{j=1}^i a_j =1) = 1-\dfrac{\sum\limits_{a_j \leq m} [\gcd\limits_{j=1}^i a_j=1]}{m^i} = 1-\dfrac{\sum\limits_{d=1}^m \mu(d)\lfloor \dfrac{m}{d}\rfloor ^i}{m^i}。 \)
所以 \(E(x)-1=\displaystyle\sum\limits_{i\geq 1}1-\dfrac{\sum\limits_{d=1}^m \mu(d)\lfloor \dfrac{m}{d}\rfloor ^i}{m^i}=-\sum\limits_{i\geq 2}\dfrac{\sum\limits_{d=1}^m \mu(d)\lfloor \dfrac{m}{d}\rfloor ^i}{m^i}=-\sum\limits_{d=1}^m \mu(d)\sum\limits_{i \geq 2} \dfrac{ \lfloor \dfrac{m}{d} \rfloor^i}{m^i}\)。
最后项可以等比数列求和，做到 \(O(n)\)。
事实上显然可以杜教筛到 \(O(n^{\frac 23})\)。
-
Method 2：自然的 dp
设 \(f_i\) 表示当前 \(\gcd\) 为 \(i\)，还期望需要多少步结束，由于 \(\gcd\) 的单调性，转移顺序是显然的。
有 \(f_i = 1+ \dfrac 1m \displaystyle\sum\limits_{\gcd(i,j)=k} f_k=1+\dfrac 1m\sum\limits_{k \mid i}f_k\sum\limits_{d \mid \frac ik}\mu(d)\lfloor \dfrac{\dfrac mk}{d}\rfloor\)，暴力计算即可。
有 \(\sum\limits_{i \leq m} \dfrac mi \sum\limits_{j \leq \frac mi} \dfrac{\dfrac mi}{j} = \sum\limits_{i \leq m} \dfrac mi \ln \dfrac mi < \sum\limits_{i \leq m} \dfrac mi \ln m = m\ln^2 m\)，所以复杂度上界是 \(O(m \ln^2m)\)。
