【题解】CF379E | 关于带权二分优化dp的一点理解

一. 问题引入 | 暴力dp

为了叙述方便：

#define A 宝贝球
#define B 超级球

同时为了避免歧义，我们令 \(qwq\) 为题目中的 \(b\)

设 \(f_{i,j,k}\) 表示前 \(i\) 个 Pokemon ，用了 \(j\) 个 A 以及 \(k\) 个 B 的最大期望。

转移方程显然：

\[f_{i,j,k}=\max \{f_{i-1,j,k},f_{i-1,j-1,k}+a_i,f_{i-1,j,k-1}+b_i,f_{i-1,j-1,k-1}+1-(1-a_i)(1-b_i) \} \]

答案为 \(f_{n,q,qwq}\) 复杂度 \(O(n^3)\)

二. WQS二分 | 优化

在平面上选出形如 \((m,f_{n,a,m})\) 的若干个点，显然其为凸函数（如果多选一个球，期望是增加的，球用的越多，期望增的越慢），但是我们不能直接求出该凸函数的样子（直接求就是上面的暴力），而我们需要知道的为该函数在 \(m=qwq\) 时的取值，于是我们考虑通过其他方式确定 \(y_m\)。

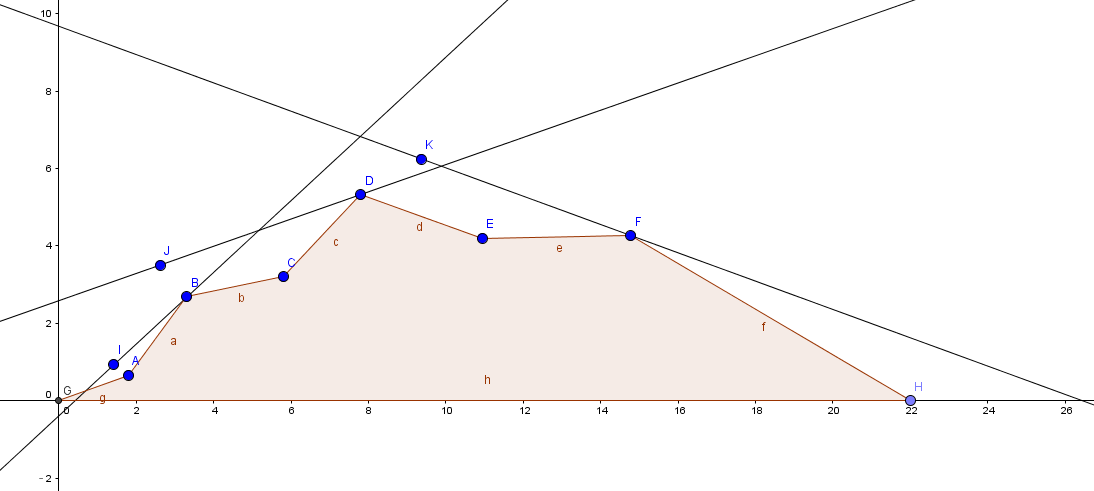
由于其凸函数的性质，那么任意引一条直线，当该函数过图像上一点且在 \(y\) 轴上的截距取到最大值时，此直线与该函数图像相切（如图）。

（图片来源于 Creeper_LKF 大佬的博客）

设该直线斜率为 \(k\)，那么可设该直线方程为： \(f_{n,a,m}=km+b\)，则有：\(b=f_{n,a,m}-km\)，如果我们能对于一个 \(k\) 快速求出 \(b\) 的最大值（\(m\) 为自变量）以及取到最大值时 \(m\) 的值，那么我们就能求出该直线与该函数的切点横坐标 \(x\)（\(x=m\)）。如果 \(x<qwq\)，由于凸函数的性质，我们可以适当减小该直线的斜率使其切点右移，同理，如果 \(x>qwq\)，我们可以适当增大该直线的斜率使其切点左移，这个调大调小的过程可以使用二分，保证了算法的复杂度正确。当二分完毕的时候，我们便得到了\(x=qwq\) 的时候的 \(k\) 以及 \(b\)，便可求出 \(f_{n,a,qwq}\)，也就是我们要求的答案。

于是问题转化为求 \(f_{n,a,m}-km\) 的最大值，其中 \(m\) 可任取。
考虑设 \(g_{i,j}=\max\limits_{m} \{ f_{i,j,m}-km \}\)，那么关于 \(g\) 的转移方程可以写成：

\[g_{i,j}=\max \{g_{i-1,j},g_{i-1,j-1}+a_i,g_{i-1,j}+b_i-k,g_{i-1,j-1}+1-(1-a_i)(1-b_i)-k \} \]

而 \(m\) 就是 \(g_{n,a}\) 从第三、四中情况转移过来的次数（可以理解为每用一个 B ，都要携带一个权值 \(k\)），可以在 dp 过程中很好维护。（代码中的 cnt[i][j]表示 \(g_{i,j}\) 从第三、四中情况转移过来的次数）。

上述过程可以在 \(O(n^2)\) 的时间内完成。

我们来梳理一下算法流程：

• 在外层二分 \(k\)
• 对于一个确定的 \(k\)，以 \(O(n^2)\) 的复杂度求出 \(g_{n,a}\) ，也即 \(b=f_{n,a,m}-km\) 的最大值，同时在这个过程中求出使 \(b\) 取到最大值的 \(m\)。
• 如果 \(x<qwq\)，往小二分
• 同理，如果 \(x>qwq\)，往大二分
• 最终当 \(x=qwq\)，求得答案

总复杂度 \(O(n^2 \log n)\)

代码

const int N=2050;
int n,a,b,cnt[N][N];
double p[N],q[N],g[N][N];
inline bool check(double k)
{
	memset(g,0,sizeof(g)),memset(cnt,0,sizeof(cnt));
	fr(i,1,n) fr(j,0,a)
	{
		g[i][j]=g[i-1][j],cnt[i][j]=cnt[i-1][j];
		if(j!=0&&g[i-1][j-1]+p[i]>=g[i][j]) g[i][j]=g[i-1][j-1]+p[i],cnt[i][j]=cnt[i-1][j-1];
		if(g[i-1][j]+q[i]-k>=g[i][j]) g[i][j]=g[i-1][j]+q[i]-k,cnt[i][j]=cnt[i-1][j]+1;
		if(j!=0&&g[i-1][j-1]+p[i]+q[i]-p[i]*q[i]-k>=g[i][j]) g[i][j]=g[i-1][j-1]+p[i]+q[i]-p[i]*q[i]-k,cnt[i][j]=cnt[i-1][j-1]+1;
	}
	return cnt[n][a]<=b;
}
int main(void)
{
	n=read(),a=read(),b=read();
	fr(i,1,n) scanf("%lf",&p[i]);
	fr(i,1,n) scanf("%lf",&q[i]);
	double l=0,r=1;int lim=60;
	while(lim--)
	{
		double mid=(l+r)/2;
		if(check(mid)) r=mid;
		else l=mid;
	}
	double k=l;//最后二分出来的斜率 
	printf("%.5lf\n",g[n][a]+k*b);//因为最后二分出来的 m 为 b 
	return 0;
}

三. 一点总结

带权二分适用于如下问题：

求出限制取某种东西的个数恰好为 \(x\)（可设 \(f_x\) 为恰好用 \(x\) 个时的最值），在这个限制下的最值，同时要求由若干个形如 \((x,f_x)\) 的点构成的函数具有凸性。

四. 关于正确性的一点证明

事实上，我们发现这个函数的凸性似乎一点用都没有。因为即使这个函数不是凸函数（甚至没有单调性也可以），也照样能满足“直线斜率减小使切点右移，直线斜率增大使切点左移”，那么，问题到底出在哪里呢？

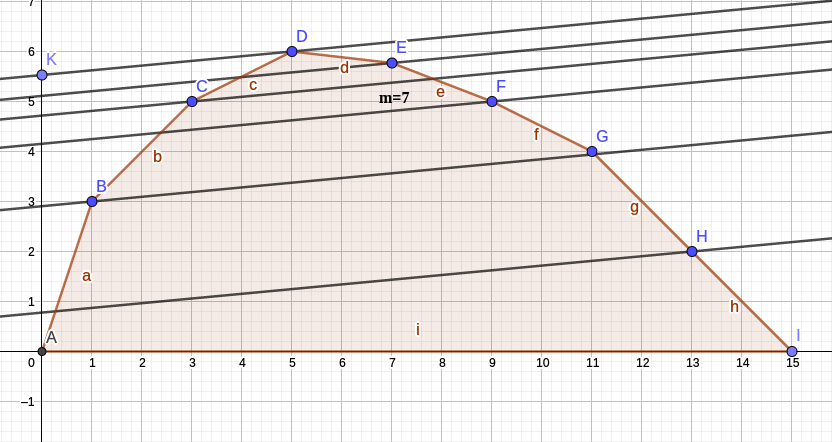
观察下图，事实上，当直线斜率变小的时候，切点依次为 \(B,D,F\) ，我们发现不在凸壳上的点其实是没有被考虑到的，所以答案的点有可能根本二分不到。（这也是许多网上的感性理解没有谈到的问题，“附加权值”变大或变小，可能导致最优决策点从来没有考虑到我们限制的那个位置）

为了满足所有点都在凸壳上，我们便要求它为一个凸函数。

（自己画的图好丑哇）

根据此，我们可以对 WQS 分治作一点没用的推广：我们只需保证答案所在的点在所有点形成的凸壳上即可，单调性与凸性其实只是这个的充分条件。
（这只是个人思考得出的结论，不保证正确性 /kk）