树状数组学习笔记
目录
-
原理（结构）
-
建树
-
应用
-
单点修改，区间求和
-
区间修改，单点求值
-
区间修改，区间求和
-
单点修改，区间求最值
-
求逆序对个数
-
二维树状数组
-
trick：树状数组上倍增
-
权值树状数组
-
正文
1. 原理
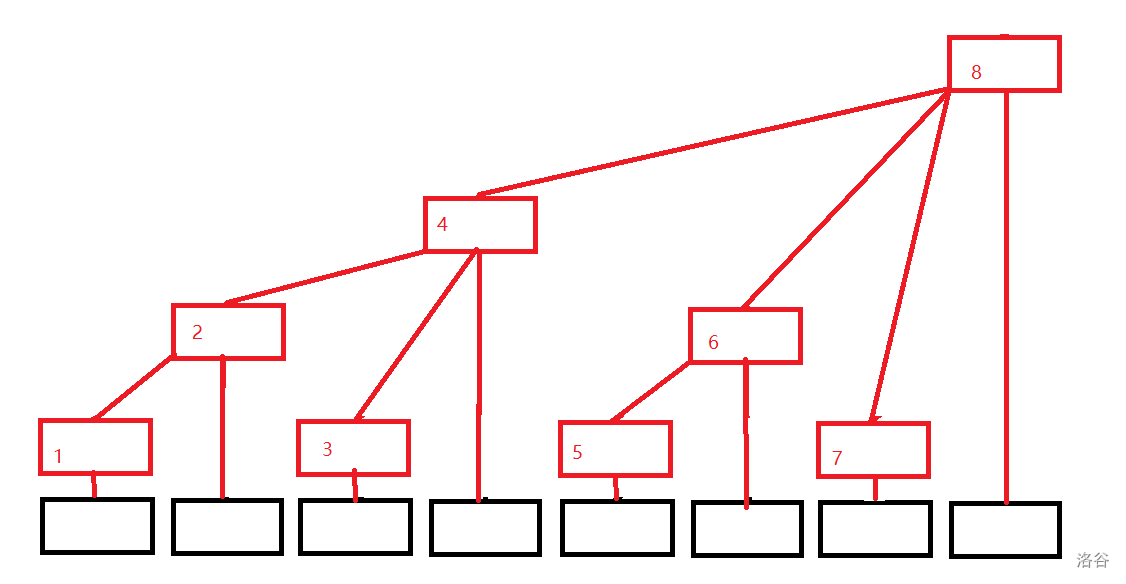
引用日报图片。
设黑色框内数组为 \(a_1 \to a_8\).
可以推得 \(c_i=a_{i-2^k+1}+a_{i-2^k+2}+...+a_i\)，其中 \(k\) 为 \(i\) 的二进制最低位到最高位连续零的长度
问题转变为求出二进制中从最低位到高位连续零的长度。
此时，我们引入 lowbit(x)=x&(-x) 。
其实可以发现，树状数组其实就是对原数组做一个特殊的前缀和，使得其可以 \(O(\log n)\) 修改和查询。
2. 建树
一般使用 \(n\) 次修改，时间复杂度为 \(O(n\log n)\)，不影响总复杂度。
但有两种方法可以达到 \(O(n)\)。
- 根据定义，\(c_i\) 表示区间 \([i-\operatorname{lowbit}(i)+1,i]\) 的和，可以直接前缀和。
for(int i=1;i<=n;i++)a[i]+=a[i-1],tr[i]=a[i]-a[i-(i&-i)];
-
算贡献。这个结合代码理解比较好。
for(int i=1;i<=n;i++) { scanf("%d",&a[i]); for(int j=1;j<lowbit(i);j*=2){ a[i]+=a[i-j]; } }for(int i=1;i<=n;i++){ scanf("%lld",&x); a[i]+=x; if(i+lowbit(i)<=n)a[i+lowbit(i)]+=a[i];//注意这里的条件 }两个代码等价，所以复杂度为 \(O(n)\)。显然也可以直接算一下第一个的大小，发现是 \(O(n)\) 的。
3. 应用
1）单点修改，区间求和
最基本的应用。
ll qry(int x) { ll ans=0; for(; x; x-=lowbit(x)) ans+=tr[x]; return ans; } void upd(int x,ll y) { for(; x<=n; x+=lowbit(x)) tr[x]+=y; }
2）区间修改，单点查询
显然可以记 b 数组为原数组的差分数组，然后在区间 \([l,r]\) 加 \(x\) 就是在 \(l\) 位置加 \(x\) ，在 \(r+1\) 位置减去 \(x\)。
3）区间修改，区间查询
记原数组 \(a\) 的差分数组为 \(b\)，则 \(a_i=\sum_{j=1}^ib_j\)。
同时维护 \(b_i,(i-1)b_i\) 即可。
int a[maxn],b[maxn],ib[maxn],n,m;
ll query(int x) {
ll ans=0;
int z=x;
for(; x; x-=lowbit(x)) ans+=z*b[x]-ib[x];
return ans;
}
void upd(int x,ll y) {
int z=x;
for(; x<=n; x+=lowbit(x)) b[x]+=y,ib[x]+=y*(z-1);
}
4）单点修改，区间最值
有点抽象，直接背板。
ll a[maxn],tr[maxn];
const ll INF=1e10;
int n,m;
void upd(int x,ll y) {
for(; x<=n; x+=lowbit(x)) tr[x]=max(tr[x],y);
}
ll query(int l,int r) {
ll res=-INF;
for(; r>=l&&r-l+1>=lowbit(r); r-=lowbit(r)) res=max(res,tr[r]);
while(r>=l) {
res=max(res,a[r]);
if(r-l+1<lowbit(r)) r--;
else res=max(res,tr[r]),r-=lowbit(r);
}
return res;
}
5）求逆序对/顺序对
给出逆序对代码。
struct element {
ll val;
int id;
bool operator < (element x) const {
return x.val<val;
}
} a[maxn];
int n,b[maxn],tr[maxn];
ll query(int x) {
ll ans=0;
for(; x; x-=lowbit(x)) ans+=tr[x];
return ans;
}
void upd(int x,int o) {
for(; x<=n; x+=lowbit(x)) tr[x]+=o;
}
void solve() {
cin>>n;
for(int i=1; i<=n; i++) cin>>a[i].val,a[i].id=i;
stable_sort(a+1,a+n+1);
for(int i=1; i<=n; i++) b[a[i].id]=i;
ll ans=0;
for(int i=n; i; i--) {
upd(b[i],1);
ans+=query(b[i]-1);
}
cout<<ans<<'\n';
}
6）二维树状数组
Useless algorithm！！！！！！！！！！！！！！！！111
7）树状数组上倍增
一个很神的 trick，可以在 \(O(\log n)\) 的时间内在树状数组上二分。
开始二分，设初始位置为 \(r\)，\(sum=\sum\limits_{i=1}^r tr_i\)，要求的数记为 \(ans\)。
考虑依次跳 \(2^{\log n},2^{\log n-1},...,2^0\) 个单位，方式如下：如果跳的这位更新后 \(>ans\)，则不更新，否则更新。也就是说，时刻保证 \(\sum\limits_{i=1}^r tr+i\le y\)。
发现往后跳的段都是诸如 \([r+1,r+2^k]\) 的段，显然树状数组可以 \(O(1)\) 统计。
例题：P6619 [省选联考 2020 A/B 卷] 冰火战士。
Solve
发现因为冰、火战士的特殊性，对冰、火战士的温度从小到大排序后，可用的冰战士是所有冰战士的一段前缀，可用火战士是所有火战士的一段后缀。
考虑记 \(f(x)\) 表示温度为 \(x\) 时消耗的总能量之和，不难发现 \(f(x)\) 等于两边能量的最小值乘二，这是一个单峰函数。
则答案在单峰函数的峰顶左右两侧。考虑二分找到最大的 \(x\) 使得 \(\sum ice_x<\sum fire_x\) 和最大的 \(y\) 使得 \(\sum\limits_{i=1}^{x+1}fire_{i}=\sum\limits_{i=1}^yfire_i\)。
显然答案不是 \(x\) 就是 \(y\)，随便算下就行了。
8）权值树状数组
使用条件：值域小 或 不强制在线（不强制在线时可以离散化）
假设维护一个桶 \(t\)，大小为值域（这就是为啥要离散化）。
-
插入一个数。即桶内这个位置加1。
-
删除一个数。即桶内这个位置减1。
-
求 \(x\) 的排名。即求 \((\sum\limits_{i=1}^{x-1}t_i)+1\)。
-
求排名为 \(x\) 的数。
记 \(f(x)\) 表示 \(x\) 的排名。则 \(f(x)=(\sum\limits_{i=1}^{x-1}t_i)+1\)。
我们需要找到最大的 \(y\) 使得 \(f(y)\le x\)。可以用到上面树状数组上倍增的技巧，时间复杂度仍然为 \(O(\log n)\)。
int kth(int k,int r) {//r为开始二分的位置 int t=0; //w 为值域 for(int i=__lg(w),x,y; i>=0; i--) { if((x=r+(1<<i))>w) continue; if((y=(t+tr[x])<k) r=x,t=y; } return r+1; }- 求 \(x\) 的前驱，即求 \(\operatorname{kth}(\operatorname{rnk}(x)-1)\)。
- 求 \(x\) 的后继，即求 \(\operatorname{kth}(\operatorname{rnk}(x+1))\)。
给出参考实现 by diqiuyi：
#include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
int n,a[maxn],t[maxn],cnt,tot;
pair<int,int> p[maxn];
#define lowbit(x) (x&(-x))
inline void Add(int x,int val) {
for(; x<=cnt; x+=lowbit(x))
t[x]+=val;
}
inline int query(int x) {
int res=0;
for(; x; x-=lowbit(x))
res+=t[x];
return res;
}
inline int rnk(int x) {
int res=0,sum=0;
for(int i=17; ~i; i--)
if(res+(1<<i)<=cnt&&sum+t[res+(1<<i)]<x)
sum+=t[res+(1<<i)],res+=(1<<i);
return res+1;
}
int main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1; i<=n; i++) {
cin>>p[i].first>>p[i].second;
if(p[i].first^4) a[++tot]=p[i].second;
}
sort(a+1,a+tot+1);
cnt=unique(a+1,a+tot+1)-a-1;
for(int i=1; i<=n; i++)
if(p[i].first^4)
p[i].second=lower_bound(a+1,a+cnt+1,p[i].second)-a;
for(int i=1; i<=n; i++) {
if(p[i].first==1) Add(p[i].second,1);
else if(p[i].first==2) Add(p[i].second,-1);
else if(p[i].first==3) cout<<query(p[i].second-1)+1<<'\n';
else if(p[i].first==4) cout<<a[rnk(p[i].second)]<<'\n';
else if(p[i].first==5) cout<<a[rnk(query(p[i].second-1))]<<'\n';
else cout<<a[rnk(query(p[i].second)+1)]<<'\n';
}
return 0;
}
