差分与前缀和 学习笔记

前缀和

一维前缀和

前缀和指数列前 \(n\) 项和，比如数组 \(a\) 的前缀和为 \(sum_i=\sum_{j=1}^ia_j\)。可以通过递推计算前缀和：

for(int i=1;i<=n;i++)sum[i]=sum[i-1]+a[i];

前缀和可以做到 \(O(1)\) 查询静态区间和，区间 \([l,r]\) 的和 \(\sum_{i=l}^l a_i=\sum_{i=1}^ra_i-\sum_{i=1}^{l-1}a_i=sum_r-sum_{l-1}\)。通过前缀和预处理可以大大减少复杂度。

与前缀和相对，也存在后缀和。只要这个运算有结合律、逆运算，就可以通过这种方式求一段区间的信息。

二维前缀和

拓展到二维上，前缀和就变成某一个位置与其左上角的和。推一下递推式，简单容斥：

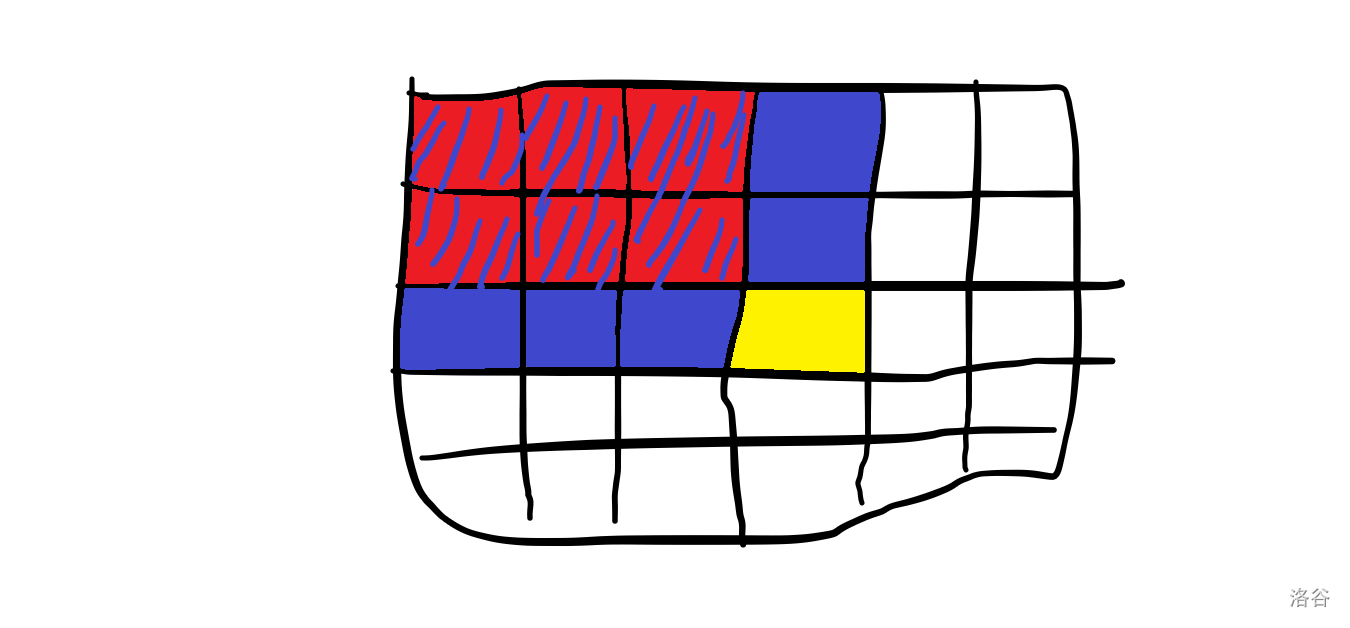
求 \(sum_{i,j}\)，先尝试用两个蓝色部分 \(sum_{i-1,j},sum_{i,j-1}\) 凑，红色部分 \(sum_{i-1,j-1}\) 算了两遍要减掉，最后加上 黄色 \(a_{i,j}\) 即可。

for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];

查询左上角为 \((x_1,y_1)\)，右下角为 \((x_2,y_2)\) 的子矩形和，仿照上面的过程，结果是 \(sum_{x_2,y_2}-sum_{x_1-1,y_2}-sum_{x_2,y_1-1}+sum_{x_1-1,y_1-1}\)。

树上前缀和

树上前缀和是一个结点到根节点路径上的权值和，可以对树 DFS 求：

void dfs(int pos,int fa){
  sum[pos]+=sum[fa];
  for(int i=0;i<e[pos].size();i++)if(e[pos][i]!=fa)dfs(e[pos][i],pos);
}

求出树上前缀和后可以 \(O(1)\) 查询树上路径的权值和。分为两种情况：

把树上路径按 \(lca\) 拆成两段。如果维护点权，那么 \(lca\) 不能减两次，\(u\to v\) 路径上的权值和为 \(sum_u+sum_v-sum_{lca(u,v)}-sum_{fa_{lca(u,v)}}\)；

如果维护边权，可以将边权放到深度较大的端点上。此时树上路径就不包括 \(lca\)，\(u\to v\) 路径上的权值和为 \(sum_u+sum_v-2sum_{lca(u,v)}\)；

高维前缀和

考虑另一种求前缀和的方式：枚举每一维，在之前的结果之上对这一维做前缀和。

for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)a[i][j]+=a[i-1][j];
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)a[i][j]+=a[i][j-1];

在维数高的时候，这样做会有很大优化。

一个应用是子集 DP：有一个长 \(2^n\) 的数组 \(a\)，要求另一个数组 \(sum\)，\(sum\) 的每一项都是其下标在二进制下子集的 \(a\) 之和。即 \(sum_i=\sum_{j\operatorname{and}i=i}a_j\)。直接枚举每个数的子集是 \(O(3^n)\) 的。然而可以把每一位看作一维，每一维只有 \(0,1\)，原来的下标中的每一位对应一维的下标。此时 \(sum\) 就是 \(a\) 的高维前缀和。

for(int i=0;i<n;i++)for(int j=0;j<(1<<n);j++)if(j>>i&1)a[j]+=a[j^(1<<i)];

另一个应用是狄利克雷前缀和：有一个数组 \(a\)，求数组 \(sum\)，\(sum_i=\sum_{j\mid i}a_j\)。类似，可以把每个质数看作一维，下标就是该质因数的次数。

for(int i=1;i<=cnt;i++)for(int j=1;prime[i]*j<=n;j++)a[prime[i]*j]+=a[j];

差分

一维差分

差分可以看作前缀和的逆运算，一维差分就是相邻两项的差：

for(int i=1;i<=n;i++)d[i]=a[i]-a[i-1];

差分可以 \(O(1)\) 表示区间修改。将区间 \([l,r]\) 加上 \(x\)，其差分数组有 \(d_l\gets d_l+x,d_{r+1}\gets d_{r+1}+x\)。

不难发现差分数组做一遍前缀和又会变回原数组。差分数组有时可以处理在原序列上不好进行的区间操作，例如对一个序列多次区间加，最后输出原数组。可以在差分数组上操作，最后再转回原数组。

二维差分

差分可以看作前缀和的逆运算，那么二维差分就是 \(d_{i,j}=a_{i,j}-a_{i-1,j}-a_{i,j-1}+a_{i-1,j-1}\)。

二维差分中修改子矩阵： \(d_{x_2+1,y_2+1}\gets d_{x_2+1,y_2+1}+x,d_{x_1,y_2+1}\gets d_{x_1,y_2+1}-x,d_{x_2+1,y_1}\gets d_{x_2+1,y_1}-x,d_{x_1,y_1}\gets d_{x_1,y_1}+x\)

树上差分

树上差分则可以表示树上路径修改，同样分为维护点权和边权两种。树上差分的意义可以看作节点的权值减去所有儿子的权值。因此把树上差分变回原数组做的是子树和。

如果是加路径上的点权，需要带上 \(lca\)：\(sum_u\gets sum_u+x,sum_v\gets sum_v+x,sum_{lca(u,v)}\gets sum_{lca(u,v)}-x,sum_{fa_{lca(u,v)}}\gets sum_{fa_{lca(u,v)}}-x\)；

否则不能操作 \(lca\)：

\(sum_u\gets sum_u+x,sum_v\gets sum_v+x,sum_{lca(u,v)}\gets sum_{lca(u,v)}-2x\)。

[[杂项]]