扩展KMP 学习笔记

定义

扩展 KMP（Z 函数）可以求主串的所有后缀与模式串的最长公共前缀。

约定字符串下标以 \(1\) 为起点。定义字符串 \(t\) 的 Z 数组 \(z_i=\operatorname{lcp}(t,t[i,m])\)，即串与每个后缀的 \(lcp\)；主串 \(s\) 与模式串 \(t\) 的 Extend 数组 \(ext_i=\operatorname{lcp}(t,s[i,n])\)，就是要求的东西。

求解 Z 函数

显然 \(z_1=n\)，考虑递推。

定义位置 \(i>1\) 的 Z-box 为 \([i,i+z_i-1]\)，也就是 \(lcp\) 的区间。记当前右端点最大的 \(lcp\) 为 \([l,r]\)。分类讨论：

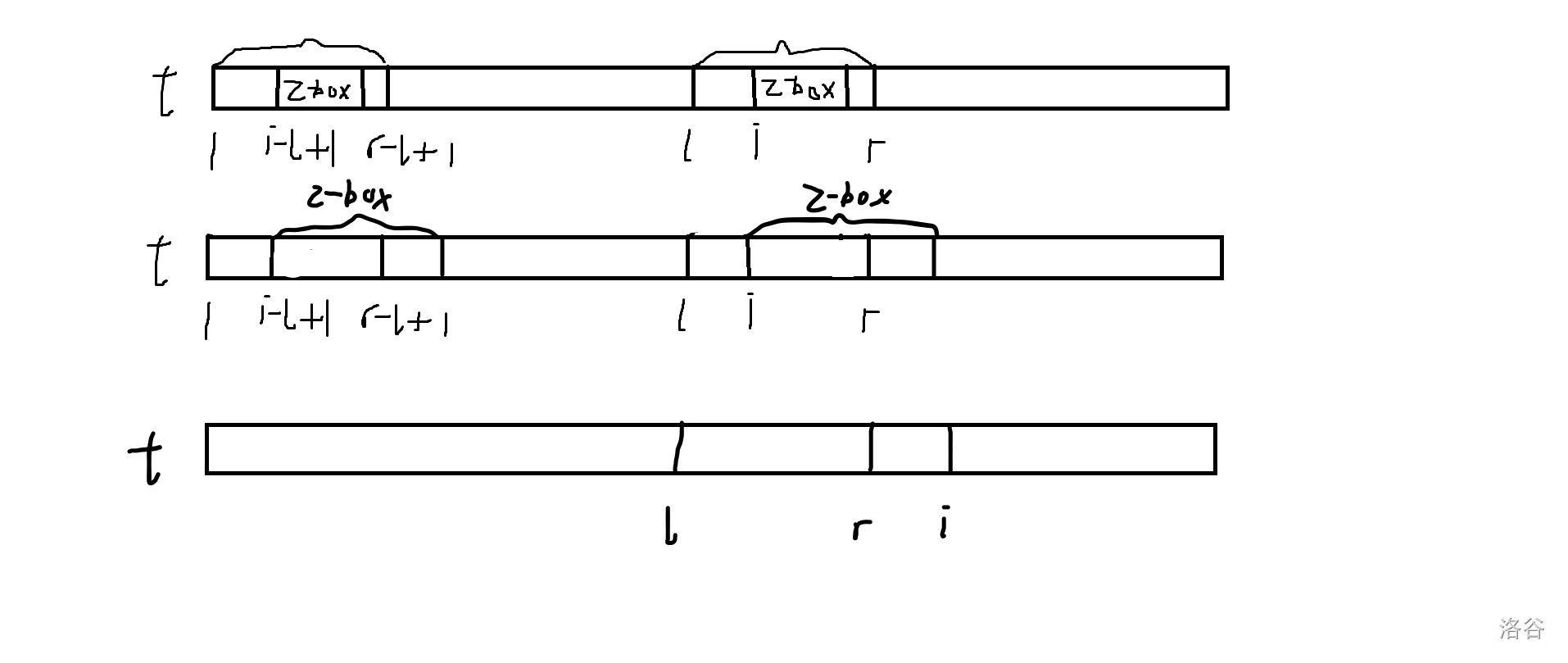
1. \(i\leq r,z_{i-l+1}<r-i+1\)

根据 Z-box 的定义，\(t[l,r]=t[1,r-l+1]\)。由于 \(z_{i-l+1}<r-i+1\)，以 \(i-l+1\) 为起点的 Z-box 属于相等的区间，可以直接移过来，\(z_i=z_{i-l+1}\)。

2. \(i\leq r,z_{i-l+1}<r-i+1\)

以 \(i-l+1\) 为起点的 Z-box 超出了区间，将 \(z_i\) 赋值为 \(r-i+1\) 再暴力往后枚举。

3. \(i>r\)

直接往后枚举。

void getz(int m,char t[],int z[]){
  z[1]=m;
  for(int i=2,l=0,r=0;i<=m;i++){
    if(i<=r)z[i]=min(z[i-l+1],r-i+1);
    while(i+z[i]<=m&&t[i+z[i]]==t[1+z[i]])z[i]++;
    if(i+z[i]-1>r)l=i,r=i+z[i]-1;
  }
}

复杂度证明：while 每执行一次 \(r\) 会增加 \(1\)，但是 \(r\leq m\)，因此复杂度线性。

求解 Extend

类似地，可以定义 Ext-box 为 \([i,i+ext_i-1]\)。

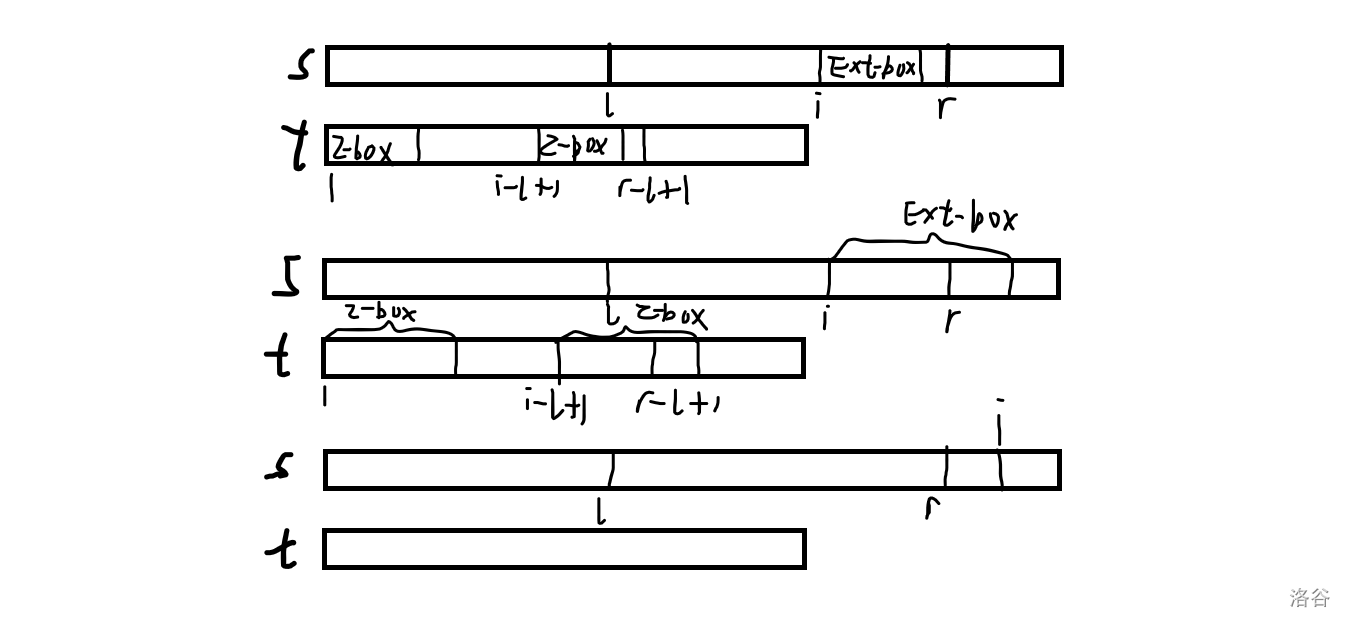
1. \(i\leq r,z_{i-l+1}<r-i+1\)

根据 Ext-box 的定义，\(s[l,r]=t[1,r-l+1]\)。由于 \(z_{i-l+1}<r-i+1\)，以 \(i-l+1\) 为起点的 Z-box 属于相等的区间，可以直接移过来，\(ext_i=z_{i-l+1}\)。

2. \(i\leq r,z_{i-l+1}<r-i+1\)

以 \(i-l+1\) 为起点的 Z-box 超出了区间，将 \(ext_i\) 赋值为 \(r-i+1\) 再暴力往后枚举。

3. \(i>r\)

直接往后枚举。

void exkmp(int n,char s[],int m,char t[],int z[],int ext[]){
  for(int i=1,l=0,r=0;i<=n;i++){
    if(i<=r)ext[i]=min(z[i-l+1],r-i+1);
    while(i+ext[i]<=n&&s[i+ext[i]]==t[1+ext[i]])ext[i]++;
    if(i+ext[i]-1>r)l=i,r=i+ext[i]-1;
  }
}

求解 \(z\) 与 \(ext\) 很相似，Z 函数可以看作模式串自己与自己作 exKMP。

[[字符串]]