AC自动机 学习笔记
自动机
OI 中所说的“自动机”一般都指“确定有限状态自动机”。
自动机可以看作一张图,有五个组成部分:字符集 \(\sum\)、状态集合 \(Q\)、起始状态 \(s\)、接受状态集合 \(F\)、转移函数 \(\delta\)。
字符集可以输入一个串,这个串的字符属于字符集。状态从起始状态转移。转移函数有两个参数:状态和输入的字符,表示这个状态输入字符后会走到哪里。每次按顺序输入一个字符转移,如果最后停在接受状态之一,则称自动机接受这个串,否则不接受。
Trie 是一个自动机,只接受已经插入的串。状态集合是树上的节点,表示串的前缀;起始状态为根;接受状态集合为叶节点;转移函数就是沿着边转移。
KMP 也可以看作一个自动机,只接受以模式串为后缀的串,状态为 \(j\),接受状态为 \(|t|\)。
定义
AC 自动机是一种多模式匹配算法,即给定多个模式串与一个主串匹配。
考虑构建一个自动机,只接受以模式串之一结尾的串。首先把所有模式串插入 Trie。
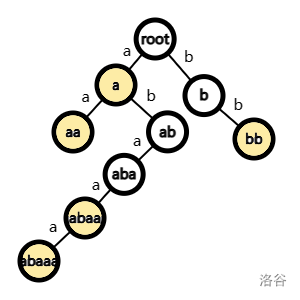
每个节点还需要一个失配指针 fail 表示在这个位置失配后回溯的位置。一个简单的想法是回溯到根,但是这样是错误的。比如在 abaa 处失配,可以回溯到 aa。因此 fail 应该指向的状态是当前状态的最长真后缀。
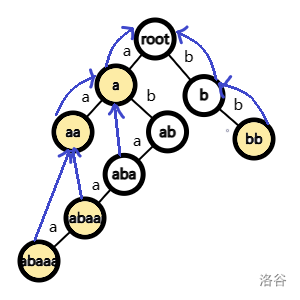
失配指针的含义和 KMP 的前缀函数类似,都是确定失配后的位置,因此 AC 自动机可以看作在 Trie 上做 KMP。
建立
和 KMP 一样考虑递推。对建好的 Trie 广搜,如果一个节点的父亲指向的节点存在一个儿子与这个节点的字符相同,那么 fail 指向这个儿子。否则就要一直沿着 fail 边跳。
然而这样做并不会向 KMP 一样均摊复杂度,寄!这样暴力跳 fail 边,过程可能产生重复,可以压缩一下跳的过程。如果子节点不存在,那么将这个节点设为父节点的 fail 下这个字符对应的节点。
比如在处理 \(aa\) 时,建出了一个虚拟节点 \(aaa\),这个节点实际上是 \(a\) 的 \(a\) 边连向的儿子,即 \(aa\)。这样在处理 \(abaaa\) 时 fail 指向 \(aaa\),即 \(aa\),可以类比一下并查集的路径压缩。
void build(){
queue<int>q;
for(int i=0;i<maxn2;i++)if(tr[0][i])fail[tr[0][i]]=0,q.push(tr[0][i]);
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=0;i<maxn2;i++){
if(tr[now][i])fail[tr[now][i]]=tr[fail[now]][i],q.push(tr[now][i]);
else tr[now][i]=tr[fail[now]][i];
}
}
}
查询
一个应用:求有多少模式串在主串出现过。
把主串输入 AC 自动机。自动机的状态是前缀,fail 边表示的是后缀,而统计的是子串,也就是前缀的后缀。那么对于经过的每一个状态暴力跳 fail 边,累加出现次数即可。
int query(string a,int pos=0,int ans=0){
for(int i=0;i<a.size();i++){
pos=tr[pos][to_num(a[i])];
for(int j=pos;j&&vis[j]!=-1;j=fail[j])ans+=vis[j],vis[j]=-1;
}
return ans;
}
这道题类似。不同的是模式串出现多次算多次,因此不用去重。
void query(string a,int pos=0){
for(int i=0;i<a.size();i++){
pos=tr[pos][to_num(a[i])];
for(int j=pos;j;j=fail[j])num[r[j]]++;
}
}
暴力跳 fail 边的深度每次至少减一,乘上外层循环,复杂度最劣 \(O(|\sum t||s|)\),在这一题中要寄。
分析一下性质:fail 边只能指向深度更小的节点,假如把所有 fail 边看作一张有向图,那么这是一张 DAG。更准确地说是一棵树,因为只有 \(n-1\) 条边。
每个节点会对其祖先产生贡献,那么先算出每个节点的经过次数,再在 fail 树上求子树和即可,深搜和拓扑排序都可。此处使用拓扑排序。
void query(string a,int ans[],int pos=0){
int deg[maxn1];
queue<int>q;
memset(deg,0,sizeof(deg));
for(int i=0;i<a.size();i++)pos=tr[pos][to_num(a[i])],ans[pos]++;
for(int i=1;i<=cnt;i++)deg[fail[i]]++;
for(int i=1;i<=cnt;i++)if(!deg[i])q.push(i);
while(!q.empty()){
int now=q.front();
q.pop(),deg[fail[now]]--,ans[fail[now]]+=ans[now];
if(!deg[fail[now]])q.push(fail[now]);
}
}
[[字符串]]


