线段树学习笔记

概述

线段树（Segment Tree）是一种常用的维护区间信息的数据结构。线段树的结构是如下的分治结构：

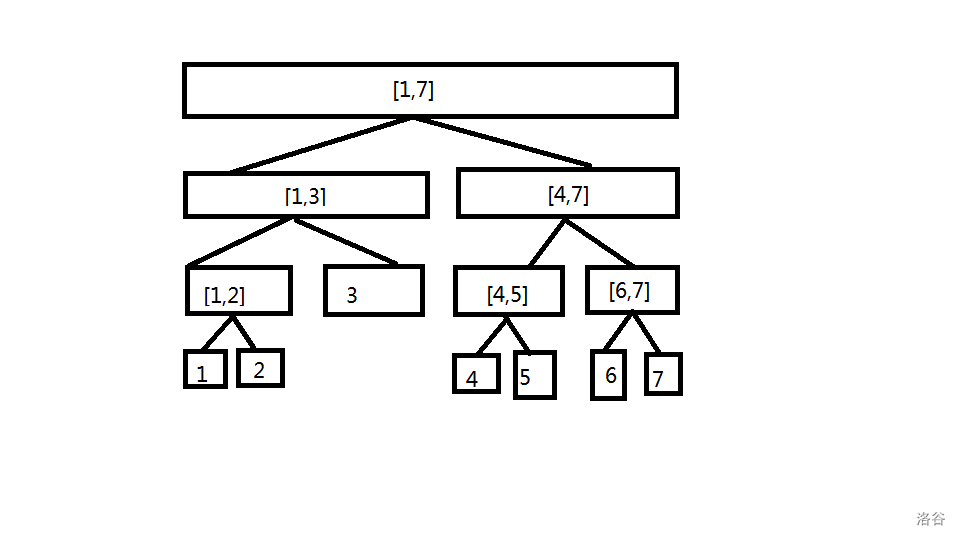
线段树是完全二叉树，每一个节点表示一个区间，将每个长度不为 \(1\) 的区间均分成左右两个区间。对于节点 \(i\)，左右儿子的编号分别为 \(2i,2i+1\)。

下面以 P3372 为例。

定义

每个节点维护两个值：\(v,tag\) 分别是维护的值和懒惰标记。其中 \(tag\) 在区间修改时会用到。

注意线段树的数组要开到原数组的四倍大小。

建树

递归建树。如果递归到叶节点就赋值，否则分治并递归，在回溯时用已经赋值的子节点更新父节点的值。

void pushup(int pos){
  tr[pos].v=tr[pos<<1].v+tr[pos<<1|1].v;
}
void build(int pos,int nl,int nr,T a[]){
  tr[pos].tag=0;
  if(nl==nr)tr[pos].v=a[nl];
  else{
    int mid=(nl+nr)>>1;
    build(pos<<1,nl,mid,a),build(pos<<1|1,mid+1,nr,a),pushup(pos);
  }
}

单点修改，区间查询

单点修改时找到叶节点更新，在回溯时 pushup。

void add(int pos,int nl,int nr,int g,T k){
  if(nl==nr){
    tr[pos].v+=k;
    return;
  }
  int mid=(nl+nr)>>1;
  if(g<=mid)add(pos<<1,nl,mid,g,k);
  if(g>mid)add(pos<<1|1,mid+1,nr,g,k);
  pushup(pos);
}

区间查询时，如果整个区间被包含在目标区间内，那么返回这个区间的值。否则需要继续往下细分。

T query(int pos,int nl,int nr,int gl,int gr){
  if(gl<=nl&&nr<=gr)return tr[pos].v;
  int mid=(nl+nr)>>1;
  T ans=0;
  if(gl<=mid)ans+=query(pos<<1,nl,mid,gl,gr);
  if(gr>mid)ans+=query(pos<<1|1,mid+1,nr,gl,gr);
  return ans;
}

区间修改，区间查询

懒惰标记

区间查询时目标区间包含当前区间可以直接返回，但是如果暴力区间修改，当前区间被包含时还要修改子树。这样如果查询 \([1,n]\) 就要把整棵树都遍历，显然要炸。

这时对这个区间打懒惰标记表示对一颗子树的修改，因为不需要用到子树的信息，所以不用修改子节点真正的值。

当需要用到子树的信息时，将标记下传给两个子节点并更新实际值，自身的标记清空，用一个函数 pushdown 表示。

void pushdown(int pos,int nl,int nr){
  int mid=(nl+nr)>>1;
  tr[pos<<1].tag+=tr[pos].tag,tr[pos<<1|1].tag+=tr[pos].tag;
  tr[pos<<1].v+=(mid-nl+1)*tr[pos].tag,tr[pos<<1|1].v+=(nr-mid)*tr[pos].tag;
  tr[pos].tag=0;
}

区间操作

区间修改：目标区间包含当前区间时，修改当前节点并打标记，直接返回。否则要往下细分并下传标记。回溯时由于不知道当前节点需要修改多少，要 pushup。

void add(int pos,int nl,int nr,int gl,int gr,T k){
  if(gl<=nl&&nr<=gr){
    tr[pos].tag+=k;
    tr[pos].v+=(tr[pos].r-tr[pos].l+1)*k;
    return;
  }
  pushdown(pos,nl,nr);
  int mid=(nl+nr)>>1;
  if(gl<=mid)add(pos<<1,nl,mid,gl,gr,k);
  if(gr>mid)add(pos<<1|1,mid+1,nr,gl,gr,k);
  pushup(pos);
}

区间查询：

类似单点修改的情况，多一个下传标记。

T query(int pos,int nl,int nr,int gl,int gr){
  if(gl<=nl&&nr<=gr)return tr[pos].v;
  pushdown(pos,nl,nr);
  int mid=(nl+nr)>>1;
  T ans=0;
  if(gl<=mid)ans+=query(pos<<1,nl,mid,gl,gr);
  if(gr>mid)ans+=query(pos<<1|1,mid+1,nr,gl,gr);
  return ans;
}

小技巧

两倍空间

上面说线段树需要开四倍空间。但是显然线段树的节点最多有 \(2n-1\) 个，下面介绍一种开两倍空间的方法：令区间 \([l,r]\) 的编号为 \((l+r)\operatorname{or}[l\ne r]\)。

叶节点的标号为偶数，其他为奇数。一个区间 \([l,r]\) 的标号为 \(2mid+1\)，左儿子的标号范围为 \([2l,2mid]\)，右儿子的标号范围为 \([2mid+2,2r]\)。因此不会重复。最大标号为 \([n,n]\) 的标号 \(2n\)。

标记永久化

标记永久化是懒惰标记之外维护区间修改的方式，不下传标记或用儿子的信息更新自身。

如果不下传标记，那么标记会影响整一棵子树。

区间修改：对于完全包含的打标记，对于不完全包含的，直接算出这个节点的区间与修改区间的交集计算影响而非 pushup。

区间查询：对于标记，由于标记不下传，每个经过的节点都要算标记与查询区间的交集的贡献。

void add(int pos,int nl,int nr,int gl,int gr,T k){
  if(gl<=nl&&nr<=gr){
    tr[pos].tag+=k;
    return;
  }
  tr[pos].v+=k*(min(nr,gr)-max(nl,gl)+1);
  int mid=(nl+nr)>>1;
  if(gl<=mid)add(pos<<1,nl,mid,gl,gr,k);
  if(gr>mid)add(pos<<1|1,mid+1,nr,gl,gr,k);
}
T query(int pos,int nl,int nr,int gl,int gr){
  if(gl<=nl&&nr<=gr)return tr[pos].v+tr[pos].tag*(nr-nl+1);
  int mid=(nl+nr)>>1;
  T ans=tr[pos].tag*(min(nr,gr)-max(nl,gl)+1);
  if(gl<=mid)ans+=query(pos<<1,nl,mid,gl,gr);
  if(gr>mid)ans+=query(pos<<1|1,mid+1,nr,gl,gr);
  return ans;
}

动态开点

当 \(n\) 很大，达到不能直接开数组的级别，可以动态开点
节约空间，当一个节点用到的时候才分配编号。

单点修改时需要多加一行 if(!pos)pos=++cnt;查询时如果节点没有建出就返回 \(0\)。如果区间修改就要在 pushdown 时也给子节点分配编号。

每个节点记录左儿子和右儿子的编号，\(pos\) 需要改为引用，这样对新建节点时，也给父节点的 \(ls,rs\) 赋值了。

一次修改最多经过 \(\log n\) 个点，一共 \(m\) 次修改，那么只需要开 \(O(m\log n)\) 的空间。

当需要开多棵线段树时，可以把线段树开在同一个数组里。

权值线段树

用线段树维护一个桶，这样的线段树叫权值线段树。

权值线段树可能出现值域过大的情况，因此可以使用动态开点。可以发现这样也自带离散化。

权值线段树也能处理负数。此时 \(mid\) 应取 \(\frac{l+r-1}{2}\)。

线段树合并

合并两棵线段树，如果有一棵树的节点没有建出就返回另一棵树上的节点，递归合并左右子树。

int merge(int a,int b,int nl,int nr){
  if(!a||!b)return a^b;
  if(nl==nr)return tr[a].v+=tr[b].v,a;
  int mid=(nl+nr)>>1;  
  tr[a].ls=merge(tr[a].ls,tr[b].ls,nl,mid),tr[a].rs=merge(tr[a].rs,tr[b].rs,mid+1,nr),pushup(a);
  return a;
}

P3224

板子题。用并查集维护连通块，每个连通块开一棵权值线段树。连边操作为线段树合并，第 \(k\) 小在这个连通块的线段树上二分。

zkw线段树

定义

zkw线段树是一种非递归的线段树，相比于递归线段树具有小常数，好码，空间小等优点，缺点是适用范围更小。

建树

zkw线段树需要先将数组长度填充成 \(2\) 的整数幂。这时这棵树为一颗满二叉树，具有很多性质。

建树时，可以利用满二叉树的性质，先对叶节点赋值，然后自底向上建树。

for(num=1;num<=n+1;num<<=1);
for(int i=1;i<=n;i++)v[num+i]=a[i];
for(int i=num-1;i>=1;i--)v[i]=v[i<<1]+v[i<<1|1];

为了方便查询，建树时需要将原数组对应的叶节点向后平移一位，并且当数组大小是 \(2\) 的整数幂或 \(2\) 的整数幂减一时，数组大小会翻倍。

单点修改，区间查询

单点修改时，直接从叶节点开始向根节点跳，修改沿途的节点。

for(x+=num;x;x>>=1)tr[x]+=k;

区间查询时，需要维护两个指针 \(l,r\)。一开始这两个指针分别指向 \([l-1,l-1],[r+1,r+1]\)，剩下要查询的区间在 \(l,r\) 中间。比如下图中 \(l,r\) 分别指向 \([2,2],[7,7]\)，表示剩下的区间为 \((2,7)\)。

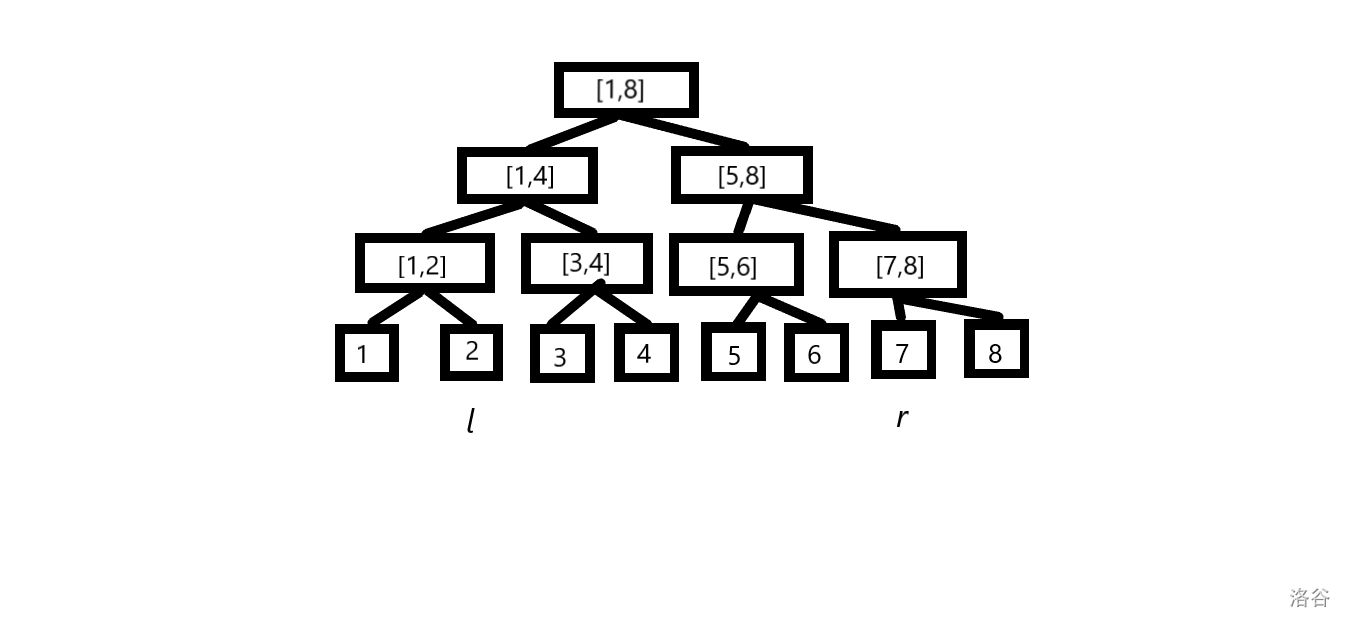
然后让 \(l,r\) 不断向上跳。对于 \(l\)，如果指向的是左儿子，那么其兄弟在当前区间内，需要统计答案。同理，如果 \(r\) 指向右儿子则统计兄弟节点的答案。当 \(l,r\) 为兄弟节点，说明剩下的区间为空，结束循环。

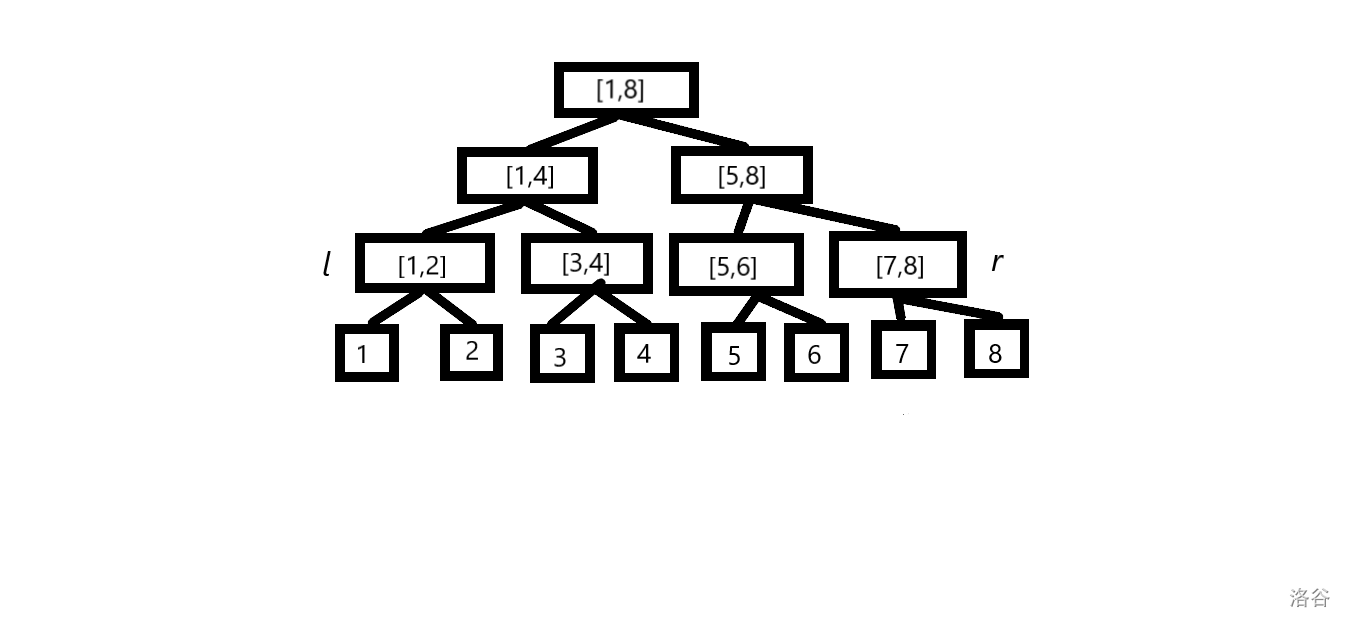
比如此时 \(l,r\) 分别指向 \([1,2],[7,8]\)，那么兄弟节点 \([3,4],[7,8]\) 在查询区间内，加入答案。然后 \(l,r\) 跳到 \([1,4],[5,8]\)，查询结束。

for(l=num+l-1,r=num+r+1;l^r^1;l>>=1,r>>=1){
  if(~l&1)ans+=tr[l^1];
  if(r&1)ans+=tr[r^1];
}
return ans;

这就解释了建树。不平移且翻倍，查询区间包括 \(1,n\) 时可能越界。

区间修改，区间查询

zkw线段树自底向上遍历，显然不能标记下传，需要使用标记永久化。

修改时遍历方法同上，对于 \(l,r\) 指向的节点修改值，兄弟节点整体修改值并打标记，表示子树需要修改。并且当这一个循环结束时，\(l,r\) 更上方的节点也需要修改，所以要继续跳到根节点。

其中 \(l,r\) 指向的节点修改的长度不固定，要开三个变量 \(cntl,cntr,len\) 表示 \(l\) 的子树修改的长度，\(r\) 的子树修改的长度，当前层区间的长度。

for(l=num+l-1,r=num+r+1;l^r^1;l>>=1,r>>=1,len<<=1){
  v[l]+=cntl*k,v[r]+=cntr*k;
  if(~l&1)v[l^1]+=len*k,tag[l^1]+=k,cntl+=len;
  if(r&1)v[r^1]+=len*k,tag[r^1]+=k,cntr+=len;
}
for(;l;l>>=1,r>>=1)v[l]+=cntl*k,v[r]+=cntr*k;

区间查询类似，需要开一个变量统计子树打标记的区间长度。由于标记不下传，有些标记可能打在更上方，需要一直跳到根节点。

for(l=num+l-1,r=num+r+1;l^r^1;l>>=1,r>>=1,len<<=1){
  ans+=cntl*tag[l]+cntr*tag[r];
  if(~l&1)ans+=v[l^1],cntl+=len; 
  if(r&1)ans+=v[r^1],cntr+=len; 
}
for(;l;l>>=1,r>>=1)ans+=cntl*tag[l]+cntr*tag[r];
return ans;

李超线段树

一种数据结构，可以动态维护平面直角坐标系上的一些线段。

P4254

板子题。有两个操作：动态插入直线，询问与直线 \(x=x_0\) 相交的已插入线段中交点 \(y\) 的最值。

这一题全是直线，可以看做左右端点取到边界的线段，相当于全局修改。每条线段转成斜截式，线段树的每个节点记录与 \(x=mid\) 的交点 \(y\) 最大的线段。

采用标记永久化，直接修改经过的每条线段。设原来的线段的斜率和截距为 \(k_0,b_0\)，新的线段为 \(k_1,b_1\)。分类讨论：

原来的线段整体在新的线段的上方，新的线段不可能更新，直接返回；
原来的线段整体在新的线段的下方，直接更新后返回；
两条线段相交，更新并用淘汰的线段递归进交点所在的儿子。

查询时递归到节点 \(y\)，由于是标记永久化要一路取 \(\max\)。

template<int maxn>struct SMT{
  int tr[maxn],cnt;
  double k[maxn],b[maxn];
  bool check(int u,int v,int x){
    return k[u]*x+b[u]>k[v]*x+b[v];
  } 
  void add(int pos,int nl,int nr,int g){
    int mid=(nl+nr)>>1;
    if(check(tr[pos],g,nl)&&check(tr[pos],g,nr))return;
    if(!check(tr[pos],g,nl)&&!check(tr[pos],g,nr)){
      tr[pos]=g;
      return;
    }
    if(check(g,tr[pos],mid))swap(g,tr[pos]);
    if(check(g,tr[pos],nl))add(pos<<1,nl,mid,g);
    else add(pos<<1|1,mid+1,nr,g);
  }
  void insert(int pos,int nl,int nr,double k,double b){
    (*this).k[++cnt]=k,(*this).b[cnt]=b,add(pos,nl,nr,cnt);
  }
  double query(int pos,int nl,int nr,int g){
    if(nl==nr)return k[tr[pos]]*g+b[tr[pos]];
    int mid=(nl+nr)>>1;
    double ans=k[tr[pos]]*g+b[tr[pos]];
    if(g<=mid)ans=max(ans,query(pos<<1,nl,mid,g));
    if(g>mid)ans=max(ans,query(pos<<1|1,mid+1,nr,g));
    return ans;
  }  
};

P4097

这一题是线段，所以是区间修改。先在线段树上拆分区间，然后按照全局修改的办法递归。复杂度 \(O(n\log^2n)\)。

template<int maxn>struct SMT{
  int tr[maxn],cnt;
  double k[maxn],b[maxn];
  bool check(int u,int v,int x){
    return fabs(k[u]*x+b[u]-k[v]*x-b[v])<1e-6?u<v:k[u]*x+b[u]>k[v]*x+b[v];
  }
  void add(int pos,int nl,int nr,int gl,int gr,int g){
    int mid=(nl+nr)>>1;
    if(gl<=nl&&nr<=gr){
      if(check(tr[pos],g,nl)&&check(tr[pos],g,nr))return;
      if(check(g,tr[pos],nl)&&check(g,tr[pos],nr)){
        tr[pos]=g;
        return;
      }
      if(check(g,tr[pos],mid))swap(g,tr[pos]);
      if(check(g,tr[pos],nl))add(pos<<1,nl,mid,gl,gr,g);
      else add(pos<<1|1,mid+1,nr,gl,gr,g);
      return;  
    }
    if(gl<=mid)add(pos<<1,nl,mid,gl,gr,g);
    if(gr>mid)add(pos<<1|1,mid+1,nr,gl,gr,g);
  }
  void insert(int pos,int nl,int nr,double k,double b){
    (*this).k[++cnt]=k,(*this).b[cnt]=b,add(pos,1,39989,nl,nr,cnt);
  }
  double query(int pos,int nl,int nr,int g){
    if(nl==nr)return tr[pos];
    int mid=(nl+nr)>>1,ans;
    if(g<=mid)ans=query(pos<<1,nl,mid,g);
    else ans=query(pos<<1|1,mid+1,nr,g);
    if(check(tr[pos],ans,g))return tr[pos];
    else return ans;
  }  
};

查询和全局修改是 \(O(\log n)\) 的。不过区间修改 \(O(\log^2 n)\)。

李超线段树是线段树的一种，所以上面线段树的操作也可应用于李超线段树。

可持久化线段树

可持久化数据结构进行操作时，还可以保存所有历史版本。

如果直接对每一个版本都建一棵树，显然时间和空间都寄。但是根据线段树的特性，每次只有 \(O(\log n)\) 级别的节点会被修改，剩下的节点可以共用剩余的点。

以 P3919 为例：

首先需要建出一棵基础树。

void build(int &pos,int nl,int nr,T a[]){
  pos=++cnt;
  if(nl==nr)tr[pos].v=a[nl];
  else{
    int mid=(nl+nr)>>1;
    build(tr[pos].ls,nl,mid,a),build(tr[pos].rs,mid+1,nr,a);
  }
}

修改时，同时在两个版本的树上递归并复制路径。

void add(int &pos,int v,int nl,int nr,int g,T k){
  tr[pos=++cnt]=tr[v];
  if(nl==nr){
    tr[pos].v=k;
    return;
  }
  int mid=(nl+nr)>>1;
  if(g<=mid)add(tr[pos].ls,tr[v].ls,nl,mid,g,k);
  else add(tr[pos].rs,tr[v].rs,mid+1,nr,g,k);
}

查询与普通线段树一样，这道题还需要将当前版本的根指向查询的版本。

P3834

如果询问全局 kth，可以用权值线段树。

对于区间问题，可以维护桶的前缀和，即对于序列的每个前缀都建一棵权值线段树，差分就可以得到一个区间的权值线段树。这需要用到可持久化线段树。

#include<bits/stdc++.h>
using namespace std;
template<typename T>struct node{
  T v;
  int ls,rs;
};
template<typename T,int maxn>struct SMT{
  node<T>tr[maxn];
  int cnt;
  void pushup(int pos){
    tr[pos].v=tr[tr[pos].ls].v+tr[tr[pos].rs].v;
  }
  void add(int &pos,int v,int nl,int nr,int g,T k){
    tr[pos=++cnt]=tr[v];
    if(nl==nr){
      tr[pos].v+=k;
      return;
    }
    int mid=(nl+nr)>>1;
    if(g<=mid)add(tr[pos].ls,tr[v].ls,nl,mid,g,k);
    else add(tr[pos].rs,tr[v].rs,mid+1,nr,g,k);
    pushup(pos);
  }
  T query(int pl,int pr,int nl,int nr,int k){
    if(nl==nr)return nl;
    int mid=(nl+nr)>>1;
    if(tr[tr[pr].ls].v-tr[tr[pl].ls].v>=k)return query(tr[pl].ls,tr[pr].ls,nl,mid,k);
    else return query(tr[pl].rs,tr[pr].rs,mid+1,nr,k-(tr[tr[pr].ls].v-tr[tr[pl].ls].v));
  }
};
SMT<int,6000005>t;
int n,m,rt[200005],a[200005],p[200005];
void rebuild(int n,int a[],int cnt=0){
  int temp[n+5];
  for(int i=1;i<=n;i++)temp[i]=a[i];
  sort(temp+1,temp+n+1),cnt=unique(temp+1,temp+n+1)-temp-1;
  for(int i=1,t;i<=n;i++)t=lower_bound(temp+1,temp+cnt+1,a[i])-temp,p[t]=a[i],a[i]=t;
}
int main(){
  cin>>n>>m;
  for(int i=1;i<=n;i++)cin>>a[i];
  rebuild(n,a);
  for(int i=1;i<=n;i++)t.add(rt[i],rt[i-1],1,n,a[i],1);
  for(int i=1,l,r,k;i<=m;i++)cin>>l>>r>>k,cout<<p[t.query(rt[l-1],rt[r],1,n,k)]<<'\n';
  return 0;
}

线段树优化建图

CF786B

这题里有对一个区间连边的操作，直接连是 \(O(n)\) 的。考虑将这些区间拆成比较少的区间，发现线段树满足这个要求。

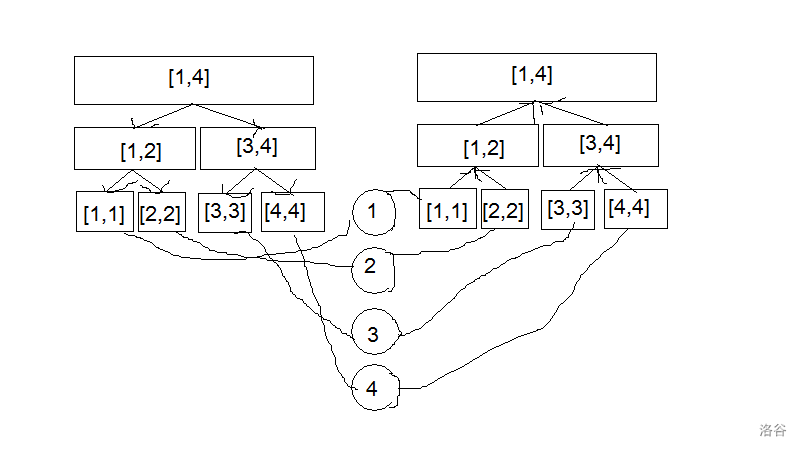
如图，建出两棵线段树，一棵由父亲向儿子连边，一棵由儿子向父亲连边，边权为零。线段树的子节点向原图的节点连双向边，边权为零。

当点向区间连边时，就把区间在第一棵线段树拆分出若干个区间，点向这些区间代表的点。这样点就可以先走到这些区间，再向下走到原图的节点。同理，区间向点连边，就在第二个线段树上拆分连向点。

边数 \(O(m\log n)\)，复杂度 \(O(m\log^2n)\)。

#include<bits/stdc++.h>
using namespace std;
int n,m,s,cnt;
long long w,dis[900005];
bool vis[900005];
vector<pair<int,long long>>e[900005];
priority_queue<pair<long long,int>,vector<pair<long long,int>>,greater<pair<long long,int>>>q;
void build(int pos,int nl,int nr){
  if(nl==nr){
    e[pos].push_back(make_pair(8*n+nl,0)),e[8*n+nl].push_back(make_pair(pos,0));
    e[4*n+pos].push_back(make_pair(8*n+nl,0)),e[8*n+nl].push_back(make_pair(4*n+pos,0));
  }
  else{
    int mid=(nl+nr)>>1;
    build(pos<<1,nl,mid),build(pos<<1|1,mid+1,nr);
    e[pos].push_back(make_pair(pos<<1,0)),e[pos].push_back(make_pair(pos<<1|1,0));
    e[4*n+(pos<<1)].push_back(make_pair(4*n+pos,0)),e[4*n+(pos<<1|1)].push_back(make_pair(4*n+pos,0));
  }
}
void add1(int pos,int nl,int nr,int gl,int gr,int u,long long w){
  if(gl<=nl&&nr<=gr){
    e[8*n+u].push_back(make_pair(pos,w));
    return;
  }
  int mid=(nl+nr)>>1;
  if(gl<=mid)add1(pos<<1,nl,mid,gl,gr,u,w);
  if(gr>mid)add1(pos<<1|1,mid+1,nr,gl,gr,u,w);
}
void add2(int pos,int nl,int nr,int gl,int gr,int u,long long w){
  if(gl<=nl&&nr<=gr){
    e[4*n+pos].push_back(make_pair(8*n+u,w));
    return;
  }
  int mid=(nl+nr)>>1;
  if(gl<=mid)add2(pos<<1,nl,mid,gl,gr,u,w);
  if(gr>mid)add2(pos<<1|1,mid+1,nr,gl,gr,u,w);
}
void dijkstra(int st,int n,vector<pair<int,long long>>e[],long long dis[]){
  for(int i=1;i<=n;i++)dis[i]=0x3f3f3f3f3f3f3f3f;
  dis[st]=0,q.push(make_pair(0,st));
  while(!q.empty()){
    int now=q.top().second;
    q.pop();
    if(vis[now])continue;
    vis[now]=1;
    for(int i=0;i<e[now].size();i++){
      int v=e[now][i].first;
      long long w=e[now][i].second;
      if(dis[v]>dis[now]+w)dis[v]=dis[now]+w,q.push(make_pair(dis[v],v));
    }
  }
}
int main(){
  cin>>n>>m>>s,cnt=n,build(1,1,n);
  for(int i=1,opt,u,l,r;i<=m;i++){
    cin>>opt;
    if(opt==1)cin>>u>>l>>w,e[8*n+u].push_back(make_pair(8*n+l,w));
    else if(opt==2)cin>>u>>l>>r>>w,add1(1,1,n,l,r,u,w);
    else cin>>u>>l>>r>>w,add2(1,1,n,l,r,u,w);
  }
  dijkstra(8*n+s,9*n,e,dis);
  for(int i=1;i<=n;i++)cout<<(dis[8*n+i]==0x3f3f3f3f3f3f3f3f?-1:dis[8*n+i])<<(i==n?'\n':' ');
  return 0;
}

P6348

区间向区间连边也类似，把两个区间都拆分，然后 \(\log n\) 个区间向 \(\log n\) 个区间连边即可。

这样做边数是 \(O(m\log^2n)\) 的。可以优化，建两个虚点中转，让 \(\log n\) 个区间向虚点连零权边，在虚点之间连一权边。这样就把边数优化到 \(O(m\log n)\)。0/1 BFS 即可。

#include<bits/stdc++.h>
using namespace std;
int n,m,s,dis[4900005];
vector<pair<int,int>>e[4900005];
bool vis[4900005];
deque<int>q;
void build(int pos,int nl,int nr){
  if(nl==nr){
    e[pos].push_back(make_pair(8*n+nl,0)),e[8*n+nl].push_back(make_pair(pos,0));
    e[4*n+pos].push_back(make_pair(8*n+nl,0)),e[8*n+nl].push_back(make_pair(4*n+pos,0));
  }
  else{
    int mid=(nl+nr)>>1;
    build(pos<<1,nl,mid),build(pos<<1|1,mid+1,nr);
    e[pos].push_back(make_pair(pos<<1,0)),e[pos].push_back(make_pair(pos<<1|1,0));
    e[4*n+(pos<<1)].push_back(make_pair(4*n+pos,0)),e[4*n+(pos<<1|1)].push_back(make_pair(4*n+pos,0));
  }
}
void add1(int pos,int nl,int nr,int gl,int gr,int u){
  if(gl<=nl&&nr<=gr){
    e[u].push_back(make_pair(pos,0));
    return;
  }
  int mid=(nl+nr)>>1;
  if(gl<=mid)add1(pos<<1,nl,mid,gl,gr,u);
  if(gr>mid)add1(pos<<1|1,mid+1,nr,gl,gr,u);
}
void add2(int pos,int nl,int nr,int gl,int gr,int u){
  if(gl<=nl&&nr<=gr){
    e[4*n+pos].push_back(make_pair(u,0));
    return;
  }
  int mid=(nl+nr)>>1;
  if(gl<=mid)add2(pos<<1,nl,mid,gl,gr,u);
  if(gr>mid)add2(pos<<1|1,mid+1,nr,gl,gr,u);
}
void bfs(int st,int n,vector<pair<int,int>>e[],int dis[]){
  for(int i=1;i<=n;i++)dis[i]=0x3f3f3f3f;
  dis[st]=0,q.push_front(st);
  while(!q.empty()){
    int now=q.front();
    q.pop_front();
    if(vis[now])continue;
    vis[now]=1;
    for(int i=0;i<e[now].size();i++){
      int v=e[now][i].first,w=e[now][i].second;
      if(dis[now]+w<dis[v]){
        dis[v]=dis[now]+w;
        if(w)q.push_back(v);
        else q.push_front(v);
      }
    }
  }
}
int main(){
  cin>>n>>m>>s,build(1,1,n);
  for(int i=1,a,b,c,d;i<=m;i++){
    cin>>a>>b>>c>>d;
    add1(1,1,n,c,d,9*n+i),add2(1,1,n,a,b,9*n+m+i),add1(1,1,n,a,b,9*n+2*m+i),add2(1,1,n,c,d,9*n+3*m+i);
    e[9*n+m+i].push_back(make_pair(9*n+i,1)),e[9*n+3*m+i].push_back(make_pair(9*n+2*m+i,1));
  }
  bfs(8*n+s,9*n+4*m,e,dis);
  for(int i=1;i<=n;i++)cout<<dis[8*n+i]<<'\n';
  return 0;
}

线段树分治

线段树分治一般用于带删除的问题，可以用一只 \(\log\) 的代价把删除变为撤销。

P5787

假如不删边，可以用种类并查集。

每条边的存在时间是一个区间。在时间轴上构建一颗线段树，将每条边按存在时间挂在线段树上。此时一个时刻存在的边就是线段树上叶子结点到祖先路径上的所有边。对线段树 DFS，在途中用并查集维护。

在回溯时，需要撤销这个节点的加边，这就将删除任意边变为撤销。用一个栈存储操作即可。

#include<bits/stdc++.h>
using namespace std;
int n,m,k,f[200005],r[200005],st[200005],top;
struct node{
  int u,v;
};
vector<node>tr[400005];
int find(int x){
  return f[x]?find(f[x]):x;
}
bool merge(int x,int y){
  int f1=find(x),f2=find(y);
  if(f1==f2)return 0;
  if(r[f1]<r[f2])f[f1]=f2,st[++top]=f1;
  else f[f2]=f1,st[++top]=f2;
  return 1;
}
void add(int pos,int nl,int nr,int gl,int gr,node k){
  if(gl<=nl&&nr<=gr){
    tr[pos].push_back(k);
    return;
  }
  int mid=(nl+nr)>>1;
  if(gl<=mid)add(pos<<1,nl,mid,gl,gr,k);
  if(gr>mid)add(pos<<1|1,mid+1,nr,gl,gr,k);
}
void dfs(int pos,int nl,int nr){
  int temp=top;
  for(int i=0;i<tr[pos].size();i++){
    merge(tr[pos][i].u,tr[pos][i].v+n),merge(tr[pos][i].v,tr[pos][i].u+n);
    if(find(tr[pos][i].u)==find(tr[pos][i].u+n)||find(tr[pos][i].u)==find(tr[pos][i].u+n)){
      for(int j=nl;j<=nr;j++)puts("No");
      goto tag;
    }
  }
  if(nl==nr)puts("Yes");
  else{
    int mid=(nl+nr)>>1;
    dfs(pos<<1,nl,mid),dfs(pos<<1|1,mid+1,nr);
  }
  tag:while(top!=temp)f[st[top]]=0,top--;
}
int main(){
  srand(time(NULL)),cin>>n>>m>>k;
  for(int i=1;i<=2*n;i++)r[i]=rand();
  for(int i=1,u,v,l,r;i<=m;i++){
    cin>>u>>v>>l>>r;
    if(++l<=r)add(1,1,k,l,r,(node){u,v});
  }
  return dfs(1,1,k),0;
}

[[数据结构]]

posted @ 2024-03-01 09:35 lgh_2009 阅读(7) 评论(0) 编辑收藏举报

刷新页面返回顶部

lgh-blog

qwq

线段树学习笔记

概述

定义

建树

单点修改，区间查询

区间修改，区间查询

懒惰标记

区间操作

小技巧

两倍空间

标记永久化

动态开点

权值线段树

线段树合并

zkw线段树

定义

建树

单点修改，区间查询

区间修改，区间查询

李超线段树

可持久化线段树

线段树优化建图

线段树分治

公告

lgh-blog

qwq

线段树 学习笔记

概述

定义

建树

单点修改，区间查询

区间修改，区间查询

懒惰标记

区间操作

小技巧

两倍空间

标记永久化

动态开点

权值线段树

线段树合并

zkw线段树

定义

建树

单点修改，区间查询

区间修改，区间查询

李超线段树

可持久化线段树

线段树优化建图

线段树分治

公告

线段树学习笔记