经典排序算法
参考地址:http://www.cnblogs.com/kkun/archive/2011/11/23/2260312.html
1,快速排序 -- Quick sort
原理,通过一趟扫描将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
实现:
1 int partition(int unsortded[],int low,int high) 2 { 3 int pivot = unsortded[low]; 4 while(low < high) 5 { 6 while(low<high && unsortded[high]>pivot) high --; 7 unsortded[low] = unsortded[high]; 8 while(low<high && unsortded[low]<pivot) low ++; 9 unsortded[high] = unsortded[low]; 10 } 11 unsortded[low] = pivot; 12 return low; 13 } 14 15 void quick_sort(int unsorted[],int low,int high) 16 { 17 int loc = 0; 18 if( low < high) 19 { 20 loc = partition(unsortded,low,high); 21 quick_sort(unsortded,low,loc-1); 22 quick_sort(unsortded,loc+1,high); 23 } 24 }
性能及优化:
快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下,每次划分将得到最坏的结果。一种比较常见的优化方法是随机化算法,即随机选取一个元素作为主元。这种情况下虽然最坏情况仍然是O(n^2),但最坏情况不再依赖于输入数据,而是由于随机函数取值不佳。实际上,随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。一位前辈做出了一个精辟的总结:“随机化快速排序可以满足一个人一辈子的人品需求。”
随机化快速排序的唯一缺点在于,一旦输入数据中有很多的相同数据,随机化的效果将直接减弱。对于极限情况,即对于n个相同的数排序,随机化快速排序的时间复杂度将毫无疑问的降低到O(n^2)。解决方法是用一种方法进行扫描,使没有交换的情况下主元保留在原位置
平衡快排:
每次尽可能地选择一个能够代表中值的元素作为关键数据,然后遵循普通快排的原则进行比较、替换和递归。通常来说,选择这个数据的方法是取开头、结尾、中间3个数据,通过比较选出其中的中值。取这3个值的好处是在实际问题中,出现近似顺序数据或逆序数据的概率较大,此时中间数据必然成为中值,而也是事实上的近似中值。万一遇到正好中间大两边小(或反之)的数据,取的值都接近最值,那么由于至少能将两部分分开,实际效率也会有2倍左右的增加,而且利于将数据略微打乱,破坏退化的结构
外部快排:
与普通快排不同的是,关键数据是一段buffer,首先将之前和之后的M/2个元素读入buffer并对该buffer中的这些元素进行排序,然后从被排序数组的开头(或者结尾)读入下一个元素,假如这个元素小于buffer中最小的元素,把它写到最开头的空位上;假如这个元素大于buffer中最大的元素,则写到最后的空位上;否则把buffer中最大或者最小的元素写入数组,并把这个元素放在buffer里。保持最大值低于这些关键数据,最小值高于这些关键数据,从而避免对已经有序的中间的数据进行重排。完成后,数组的中间空位必然空出,把这个buffer写入数组中间空位。然后递归地对外部更小的部分,循环地对其他部分进行排序。
三路基数快排:
(Three-way Radix Quicksort,也称作Multikey Quicksort、Multi-key Quicksort):结合了基数排序(radix sort,如一般的字符串比较排序就是基数排序)和快排的特点,是字符串排序中比较高效的算法。该算法被排序数组的元素具有一个特点,即multikey,如一个字符串,每个字母可以看作是一个key。算法每次在被排序数组中任意选择一个元素作为关键数据,首先仅考虑这个元素的第一个key(字母),然后把其他元素通过key的比较分成小于、等于、大于关键数据的三个部分。然后递归地基于这一个key位置对“小于”和“大于”部分进行排序,基于下一个key对“等于”部分进行排序
2 桶排序 Bucket sort
特点:
桶排序是稳定的
桶排序是常见排序里最快的一种,比快排还快(大多数情况下)
桶排序非常快,但是同时也非常耗空间,基本上是最耗空间的一种排序算法

基本实现:
1 /// 桶排序 2 int * bucket_sort(int unsorted[],int len,int maxNumber=99) 3 { 4 int *sorted = new int[maxNumber+1]; 5 for(int i = 0; i < len; i ++ ) 6 { 7 sorted[unsortded[i]] = unsorted[i]; 8 } 9 }
上面这个列子是简单的思路,肯定不实用,要想深一层了解桶排序,参考:http://www.cnblogs.com/hxsyl/p/3214379.html
桶排序主要应用在海量数据处理
3,插入排序 -- Insertion Sort
插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置,直到全部插入完毕
插入排序方法分直接插入排序和折半插入排序两种,这里只介绍直接插入排序,折半插入排序留到“查找”内容中进行

实现:
1 void insertion_sort(int unsorted[],int len) 2 { 3 for(int i = 0 ; i < len; i ++ ) 4 if(unsorted[i - 1] > unsortded[i]) 5 { 6 int temp = unsorted[i]; 7 int j = i; 8 while( j > 0 && unsortded[j-1]>temp) 9 { 10 unsortded[j] = unsortded[j-1]; 11 j --; 12 } 13 unsortded[j] = temp; 14 } 15 }
复杂度:
如果目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1)次。平均来说插入排序算法的时间复杂度为O(n^2)。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择
稳定性:
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的
4,基数排序 -- Radix Sort
原理类似桶排序,这里总是需要10个桶,多次使用
首先以个位数的值进行装桶,即个位数为1则放入1号桶,为9则放入9号桶,暂时忽视十位数,再次入桶,不过这次以十位数的数字为准,进入相应的桶
这是基本桶排序的一个升级版
实现:
1 //约定:待排数字中没有0,如果某桶内数字为0则表示该桶未被使用,输出时跳过即可 2 // unsorted 待排数组 array_x 桶数组第一维长度 array_y 桶数组第二维长度 3 void radix_sort(int unsorted[],int len,int array_x=10,int array_y=100); 4 { 5 for(int i = 0 ; i < array_x; /* 最大数字不超过999999999...(array_x个9) */ i ++ ) 6 { 7 int bucket[arry_x][array_y]; 8 for(int j = 0 ; j < len;j ++) 9 { 10 int temp = (unsortded[j]/(int)pow(10,i))%10; 11 for(int l = 0; l < array_y; l ++ ) 12 { 13 if(bucket[temp][l] == 0) 14 { 15 bucket[temp][l] = unsortded[j]; 16 break; 17 } 18 } 19 } 20 for(int o = 0,x = 0; x < array_x ; x ++ ) 21 { 22 for(int y = 0; y < array_y ; y ++ ) 23 { 24 if(bucket[x][y] == 0) continue; 25 unsorted[o ++] = bucket[x][y]; 26 } 27 } 28 } 29 }
效率分析:
时间效率[1] :设待排序列为n个记录,d个关键码,关键码的取值范围为radix,则进行链式基数排序的时间复杂度为O(d(n+radix)),其中,一趟分配时间复杂度为O(n),一趟收集时间复杂度为O(radix),共进行d趟分配和收集。 空间效率:需要2*radix个指向队列的辅助空间,以及用于静态链表的n个指针
5,鸽巢排序 -- Pigeonhole Sort
原理类似桶排序,同样需要一个很大的鸽巢[桶排序里管这个叫桶,名字无所谓了]
鸽巢其实就是数组啦,数组的索引位置就表示值,该索引位置的值表示出现次数,如果全部为1次或0次那就是桶排序
样例实现:
1 int * pogeon_sort(int unsorted[],int len,int maxNumber = 100) 2 { 3 int * pogeonHole = new int[maxNumber+1]; 4 for(int i = 0 ; i < len; i ++ ) 5 { 6 pogeonHole[unsortded[i]] ++; 7 } 8 return pogeonHole; 9 }
算法效率:
最坏时间复杂度: O(N+n)
最好时间复杂度: O(N+n)
平均时间复杂度: O(N+n)
最坏空间复杂度: O(N*n)
6,归并排序 -- Merge Sort
原理,把原始数组分成若干子数组,对每一个子数组进行排序,继续把子数组与子数组合并,合并后仍然有序,直到全部合并完,形成有序的数组

归并排序中中两件事情要做:
第一: “分”, 就是将数组尽可能的分,一直分到原子级别。
第二: “并”,将原子级别的数两两合并排序,最后产生结果。
实现:
1 void merge(int unsorted[],int first,int mid,int last,int sorted[]) 2 { 3 int i = first,j = mid; 4 int k = 0 ; 5 while( i < mid && j < last ) 6 if(unsortded[i] < unsortded[j]) 7 sorted[k++] = unsorted[i++]; 8 else 9 sorted[k++] = unsortded[j++]; 10 while( i < mid ) 11 sorted[k++] = unsorted[i++]; 12 while( j < last) 13 sorted[k++] = unsortded[j++] 14 for( int v = 0 ; v < k ; v ++ ) 15 unsorted[first + v] = sorted[v]; 16 } 17 void merge_sort(int unsorted[],int first,int last,int sorted[]) 18 { 19 if( first+1 < last ) 20 { 21 int mid = ( first + last ) / 2; 22 merge_sort(unsortded,first,mid,sorted); 23 merge_sort(unsortded,mid,last,sorted); 24 merge(unsorted,first,mid,last,sorted); 25 } 26 }
负责度:
时间复杂度为 O(nlogn) 这是该算法中最好,最坏,和平均的时间性能
空间复杂度为 O(n)
比较操作的次数介于 (nlogn)/2 和 nlongn -n + 1
赋值操作的次数是 2nlogn。
归并算法的空间复杂度为 O(n)
归并排序比较占用内存,但却是一种效率高切稳定的算法
7,冒泡排序 -- Bubble Sort
原理是临近的数字两两进行比较,按照从小到大或者从大到小的顺序进行交换,样一趟过去后,最大或最小的数字被交换到了最后一位,然后再从头开始进行两两比较交换,直到倒数第二位时结束,其余类似
实现:
1 void bubble_sort(int unsorted[],int len) 2 { 3 for(int i = 0 ; i < len; i ++ ) 4 { 5 for(int j = i ; j < len; j ++ ) 6 { 7 if( unsorted[i] > unsortded[j]) 8 { 9 int temp = unsortded[i]; 10 unsortded[i] = unsortded[j]; 11 unsortded[j] = temp; 12 } 13 } 14 } 15 }
存在不足:就是本来位于前面的较小数被交换到后面
时间复杂度:
若文件的初始状态是正序的,一趟扫描即可完成排序。所需的关键字比较次数 C 和记录移动次数 M 均达到最小值:

所以,冒泡排序的最好的时间复杂度为 O(n)
若初始文件是反序的,需要进行 n-1 趟排序。每趟排序要进行 n-i 次关键字的比较(1 <= 1 <= n-1),且每次都必须移动记录三次来达到交换记录位置。这种情况下,比较和移动次数均达到最大值:


冒泡排序的最欢时间复杂度为 O(n2)
综上,因此冒泡排序总得时间复杂度为 O(n2)
算法稳定性:
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,我想你是不会再无聊地把他们俩交换一下的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法
冒泡排序动画演示:

8,选择排序 -- Selection Sort
顾名思意,就是直接从待排序数组里选择一个最小(或最大)的数字,每次都拿一个最小数字出来,顺序放入新数组,直到全部拿完
再简单点,对着一群数组说,你们谁最小出列,站到最后边,然后继续对剩余的无序数组说,你们谁最小出列,站到最后边,再继续刚才的操作,一直到最后一个,继续站到最后边,现在数组有序了,从小到大
实现:
1 void selection_sort(int unsorted[],int len) 2 { 3 for(int i = 0; i < len; i ++ ) 4 { 5 int min = unsorted[i],min_index = i; 6 for(int j = i ; j < len; j ++ ) 7 { 8 if( unsortded[j] < min ) 9 { 10 min = unsortded[j]; 11 min_index = j; 12 } 13 } 14 if( min_index != i ) 15 { 16 int temp = unsorted[i]; 17 unsortded[i] = unsortded[min_index]; 18 unsortded[min_index] = temp; 19 } 20 } 21 }
分析:
从选择排序的思想或者是上面的代码中,我们都不难看出,寻找最小的元素需要一个循环的过程,而排序又是需要一个循环的过程。因此显而易见,这个算法的时间复杂度也是O(n*n)的。这就意味值在n比较小的情况下,算法可以保证一定的速度,当n足够大时,算法的效率会降低。并且随着n的增大,算法的时间增长很快。因此使用时需要特别注意。
9,鸡尾酒排序 -- Cocktail Sort
鸡尾酒排序是基于冒泡排序,双向循环
样例实现:
1 void cocktail_sort(int unsorted[],int len) 2 { 3 bool swapped = false; 4 do 5 { 6 for(int i = 0; i < len; i ++ ) 7 { 8 if(unsorted[i] > unsorted[i+1]) 9 { 10 int temp = unsorted[i]; 11 unsorted[i] = unsorted[i+1]; 12 unsorted[i+1] = temp; 13 swapped = true; 14 } 15 } 16 swapped = false; 17 for(int j = len; j > 1; j -- ) 18 { 19 if(unsortded[j] < unsortded[j-1]) 20 { 21 int tmep = unsorted[j]; 22 unsorted[j] = unsorted[j=1]; 23 unsortded[j-1] = temp; 24 swapped = true; 25 } 26 } 27 }while(swapped); 28 }
复杂度:
鸡尾酒排序最糟或是平均所花费的次数都是O(n²),但如果序列在一开始已经大部分排序过的话,会接近O(n)。
10,希尔排序 -- Shell Sort
希尔排序 是基于插入排序的一种改动,同样分为两部分,希尔排序和关键字的选取
(参考:http://www.cnblogs.com/jingmoxukong/p/4303279.html)
观察一下”插入排序“:其实不难发现她有个缺点:
如果当数据是”5, 4, 3, 2, 1“的时候,此时我们将“无序块”中的记录插入到“有序块”时,估计俺们要崩盘,每次插入都要移动位置,此时插入排序的效率可想而知。
shell根据这个弱点进行了算法改进,融入了一种叫做“缩小增量排序法”的思想,其实也蛮简单的,不过有点注意的就是: 增量不是乱取,而是有规律可循的

首先要明确一下增量的取法:
第一次增量的取法为: d=count/2;
第二次增量的取法为: d=(count/2)/2;
最后一直到: d=1;
看上图观测的现象为:
d=3时:将40跟50比,因50大,不交换。
将20跟30比,因30大,不交换。
将80跟60比,因60小,交换。
d=2时:将40跟60比,不交换,拿60跟30比交换,此时交换后的30又比前面的40小,又要将40和30交换,如上图。
将20跟50比,不交换,继续将50跟80比,不交换。
d=1时:这时就是前面讲的插入排序了,不过此时的序列已经差不多有序了,所以给插入排序带来了很大的性能提高。
第一块希尔排序介绍
准备待排数组[6 2 4 1 5 9]
首先需要选取关键字,例如关键是3和1(第一步分成三组,第二步分成一组),那么待排数组分成了以下三个虚拟组:
[6 1]一组
[2 5]二组
[4 9]三组
看仔细啊,不是临近的两个数字分组,而是3(分成了三组)的倍数的数字分成了一组,
就是每隔3个数取一个,每隔三个再取一个,这样取出来的数字放到一组,
把它们当成一组,但不实际分组,只是当成一组来看,所以上边的"组"实际上并不存在,只是为了说明分组关系
对以上三组分别进行插入排序变成下边这样
[1 6] [2 5] [4 9]
具体过程:
[6 1]6和1交换变成[1 6]
[2 5]2与5不动还是[2 5]
[4 9]4与9不动还是[4 9]
第一趟排序状态演示:
待排数组:[6 2 4 1 5 9]
排后数组:[1 2 4 6 5 9]
第二趟关键字取的是1,即每隔一个取一个组成新数组,实际上就是只有一组啦,隔一取一就全部取出来了嘛
此时待排数组为:[1 2 4 6 5 9]
直接对它进行插入排序
还记得插入排序怎么排不?复习一下
[1 2 4]都不用动,过程省略,到5的时候,将5取出,在前边的有序数组里找到适合它的位置插入,就是4后边,6前边
后边的也不用改,所以排序完毕
顺序输出结果:[1 2 4 5 6 9]
第二块希尔排序的关键是如何取关键字,因为其它内容与插入排序一样
那么如何选取关键字呢?就是分成三组,一组,这个分组的依据是什么呢?为什么不是二组,六组或者其它组嘞?
好的增量序列的共同特征:
① 最后一个增量必须为1
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况
参见 http://baike.baidu.com/view/2217047.htm
这么关键的问题竟然没有一个公式,只给出了两个判定标准
好吧,一般10个待排数字的话,关键依次选取5 3 1即可,其它的情况只能自己判断了,然后看是否符合上述两条"好"的标准
增量的取值规则为第一次取总长度的一半,第二次取一半的一半,依次累推直到1为止
图示如下:

实现:
1 void shell_sort(int unsorted[],int len) 2 { 3 int group,i,j,temp; 4 for(group = len/2,grop > 0; group /= 2) 5 { 6 for(i = group; i < len; i ++ ) 7 { 8 for(j = i - group; j >=0 ; j -= group ) 9 { 10 if(unsortded[j] > unsortded[j+group]) 11 { 12 temp = unsortded[j]; 13 unsortded[j] = unsortded[j + group]; 14 unsortded[j + group] = temp; 15 } 16 } 17 } 18 } 19 }
希尔排序的算法性能:
| 排序类别 | 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 | 复杂性 | ||
| 平均情况 | 最坏情况 | 最好情况 | |||||
| 插入排序 | 希尔排序 |
O(Nlog2N)
|
O(N1.5)
|
O(1)
|
不稳定 | 较复杂 | |
时间复杂度:
算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为插入排序,这就保证了数据一定会被排序。
Donald Shell 最初建议步长选择为N/2并且对步长取半直到步长达到1。虽然这样取可以比O(N2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。比如,如果一个数列以步长5进行了排序然后再以步长3进行排序,那么该数列不仅是以步长3有序,而且是以步长5有序。如果不是这样,那么算法在迭代过程中会打乱以前的顺序,那就不会以如此短的时间完成排序了。
| 步长序列 | 最坏情况下复杂度 |
|---|---|
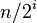 |
 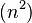 |
 |
  |
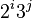 |
 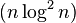 |
这项研究也表明“比较在希尔排序中是最主要的操作,而不是交换。”用这样步长序列的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
算法稳定性:
由上文的希尔排序算法演示图即可知,希尔排序中相等数据可能会交换位置,所以希尔排序是不稳定的算法。
11,堆排序 -- Heap Sort
堆排序有点小复杂,分成三块 : 什么是堆,什么是最大堆 怎么将堆调整为最大堆 堆排序
什么是堆:
这里的堆(二叉堆),指得不是堆栈的那个堆,而是一种数据结构。堆实际上是一棵完全二叉树,其任何一非叶节点满足性质:
Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2] 即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字
堆分为大顶堆和小顶堆,满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆,满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的,小顶堆的堆顶的关键字是所有关键字中最小的。
堆可以视为一棵完全的二叉树,完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示,每一个结点对应数组中的一个元素.数组与堆之间的关系

二叉堆一般分为两种:最大堆和最小堆。
最大堆:堆中每个父节点的元素值都大于等于其孩子结点(如果存在),这样的堆就是一个最大堆。因此,最大堆中的最大元素值出现在根结点(堆顶)
节点与数组索引关系:对于给定的某个结点的下标i,可以很容易的计算出这个结点的父结点、孩子结点的下标,而且计算公式很漂亮很简约

怎么将堆调整为最大堆
个过程如下图所示
在4,14,7这个小堆里边,父节点4小于左孩子14,所以两者交换
在4,2,8这个小堆里边,父节点4小于右孩子8,所以两者交换

上图展示了一趟调整的过程,这个过程递归实现,直到调整为最大堆为止
堆排序介绍:
堆排序就是把堆顶的最大数取出,将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现
剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束
下边三张图详细描述了整个过程



以下参考:http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html
.堆排序的思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
其基本思想为(大顶堆):
1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆,此堆为初始的无序区;
2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
操作过程如下:
1)初始化堆:将R[1..n]构造为堆;
2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换,然后将新的无序区调整为新的堆。
因此对于堆排序,最重要的两个操作就是构造初始堆和调整堆,其实构造初始堆事实上也是调整堆的过程,只不过构造初始堆是对所有的非叶节点都进行调整。
下面举例说明:
给定一个整形数组a[]={16,7,3,20,17,8},对其进行堆排序。
首先根据该数组元素构建一个完全二叉树,得到

然后需要构造初始堆,则从最后一个非叶节点开始调整,调整过程如下:



20和16交换后导致16不满足堆的性质,因此需重新调整

这样就得到了初始堆
即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质,因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了

此时3位于堆顶不满堆的性质,则需调整继续调整










这样整个区间便已经有序了。
从上述过程可知,堆排序其实也是一种选择排序,是一种树形选择排序。只不过直接选择排序中,为了从R[1...n]中选择最大记录,需比较n-1次,然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过,而树形选择排序恰好利用树形的特点保存了部分前面的比较结果,因此可以减少比较次数。对于n个关键字序列,最坏情况下每个节点需比较log2(n)次,因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序,不适合记录较少的排序
实现:
1 //堆排序(大顶堆) 2 void HeapAdjust(int *a,int i,int size) //调整堆 3 { 4 int lchild = 2 * i; //i的左孩子节点序号 5 int rchild = 2 * i + 1; //i的右孩子节点序号 6 int max = i; //临时变量 7 if( i < size/2 ) //如果i是叶节点就不用进行调整 8 { 9 if( lchild <= size && a[lchild] > a[max] ) 10 { 11 max = lchild; 12 } 13 if( rchild <= size && a[rchild] > a[max] ) 14 { 15 max = rchild; 16 } 17 if( max != i ) 18 { 19 swap(a[i],a[max]); 20 HeapAdjust(a,max,size); //避免调整之后以max为父节点的子树不是堆 21 } 22 } 23 } 24 void BuildHeap(int *a,int size) //建立堆 25 { 26 int i; 27 for( i=size/2; i >= 1 ; i -- ) //非叶节点最大序号值为size/2 28 29 { 30 HeapAdjust(a,i,size); 31 } 32 } 33 void HeapSort(int *a,int size) //堆排序 34 { 35 int i; 36 BuildHeap(a,size); 37 for(i = size; i >= 1; i --) 38 { 39 swap(a[1],a[i]); //交换堆顶和最后一个元素,即每次将剩余元素中的最大者放到最后面 40 HeapAdjust(a,1,i-1); //重新调整堆顶节点成为大顶堆 41 } 42 }
算法分析:
堆排序的时间,主要由建立初始堆和反复重建堆这两部分的时间开销构成,它们均是通过调用Heapify实现的
平均性能:
O(N*logN)
其他性能:
由于建初始堆所需的比较次数较多,所以堆排序不适宜于记录数较少的文件。
堆排序是就地排序,辅助空间为O(1).
它是不稳定的排序方法。(排序的稳定性是指如果在排序的序列中,存在前后相同的两个元素的话,排序前 和排序后他们的相对位置不发生变化)
12,地精排序 -- Gnome Sort
号称最简单的排序算法,只有一层循环,默认情况下前进冒泡,一旦遇到冒泡的情况发生就往回冒,直到把这个数字放好为止
实现:
1 void gnome_sort(int unsorted[],int len) 2 { 3 int i = 0; 4 while( i < len ) 5 { 6 if( i == 0 || unsortded[i-1] <= unsortded[i] ) 7 { 8 i ++; 9 } 10 else 11 { 12 int tmp = unsortded[i]; 13 unsortded[i] = unsortded[i-1]; 14 unsortded[i-1] = tmp; 15 i -- ; 16 } 17 } 18 }
模板实现:
1 template<class T> 2 void gnome_sort_1(T data[],int n,bool comparator(T,T)) 3 { 4 int i = 1; 5 while( i < n ) 6 { 7 if( i > 0 && comparator(data[i],data[i-1]) 8 { 9 swap(data[i],data[i-1]); 10 i --; 11 } 12 else 13 { 14 i ++; 15 } 16 } 17 }
优化1:
精在回头检查花盘顺序前记下当前位置,整理完就瞬间转移到之前位置的下一个位置。瞬间转移,很强大,哈哈。
实现:
1 template<class T> 2 void gnome_sort_2(T data[],int n,bool comparator(T,T)) 3 { 4 int i = 1,previous_position = -1; 5 while( i < n ) 6 { 7 if( i > 0 && comparator(data[i],data[i-1]) 8 { 9 if( previous_position == -1 ) 10 { 11 previous_position = i; 12 } 13 swap(data[i],data[i-1]); 14 i --; 15 } 16 else 17 { 18 if( previous_position == -1 ) 19 { 20 i ++; 21 } 22 else 23 { 24 i = previous_position + 1; 25 previous_position = -1; 26 } 27 } 28 } 29 }
不断把列表后面待排序的元素插入到列表前面已排序的部分中,但类似于冒泡排序那样比较并交换相邻元素。因此其算法复杂度与插入排序相当,但比插入排序需要更多的复制操作(用于交换相邻元素)。
优化2:
搬了无数花盘后,地精想到一个新方法。如果交换相邻两个花盘,每次要搬花盘三次(复制三次),如果先拿起来当前位置的花盘(temp=data[i]),就有空位给其他花盘移动,每次只搬一次花盘(复制一次,data[i]=data[i-1])。这次地精先拿一个花盘在手(temp),如果手中花盘(temp)应放到上一个花盘(i-1)前面,就用脚(地精一般不高,脚够长吗?^_^)将上一个花盘(i-1)踢到当前位置(i),然后拿着花盘(temp)走到上一个位置(i=i-1),重复此过程。
实现:(原文没有给temp初始化,也许我理解错了)
1 template<class T> 2 void gnome_sort_3(T data[],int n,bool comparator(T,T)) 3 { 4 int i = 1,previous_position = -1; 5 T temp = data[i]; 6 while( i < n ) 7 { 8 if( i > 0 && comparator(temp,data[i-1]) 9 { 10 if( previous_position == -1 ) 11 { 12 previous_position = i; 13 } 14 data[i] = data[i-1]; 15 i --; 16 } 17 else 18 { 19 if( previous_position == -1 ) 20 { 21 i ++; 22 } 23 else 24 { 25 data[i] = temp; 26 i = previous_position + 1; 27 previous_position = -1; 28 } 29 temp = data[i]; 30 } 31 } 32 }
又一个比较性质的排序,基本思路是奇数列排一趟序,偶数列排一趟序,再奇数排,再偶数排,直到全部有序
举例吧
待排数组[6 2 4 1 5 9]
第一次比较奇数列,奇数列与它的邻居偶数列比较,如6和2比,4和1比,5和9比
[6 2 4 1 5 9]
交换后变成
[2 6 1 4 5 9]
第二次比较偶数列,即6和1比,5和5比
[2 6 1 4 5 9]
交换后变成
[2 1 6 4 5 9]
第三趟又是奇数列,选择的是2,6,5分别与它们的邻居列比较
[2 1 6 4 5 9]
交换后
[1 2 4 6 5 9]
第四趟偶数列
[1 2 4 6 5 9]
一次交换
[1 2 4 5 6 9]
实现:
1 void parallel_bubblesort(void **ppData,int nDataLen,COMPAREFUNC func) 2 { 3 int i,j; 4 for(i = 0; i < nDataLen; i ++ ) 5 { 6 if( (i & 0x1) == 0 ) //i为偶数 7 { 8 for( j = 0; j < nDataLen; j += 2 ) 9 { 10 if( (*func)(ppData[j],ppData[j+1])>0 ) 11 { 12 void *pData = ppData[j]; 13 ppData[j] = ppData[j+1]; 14 ppData[j+1] = pData; 15 } 16 } 17 } 18 else 19 { 20 for(j = 1; j < nDataLen - 1; j += 2) 21 { 22 if( (*func)(ppData[j],ppData[j+1])>0) 23 { 24 void *pData = ppData[j]; 25 ppData[j] = ppData[j+1]; 26 ppData[j+1] = pData; 27 } 28 } 29 } 30 } 31 return ; 32 }
14,梳排序 -- Comb Sort
梳排序还是基于冒泡排序,与冒泡不同的是,梳排序比较的是固定距离处的数的比较和交换,类似希尔那样
这个固定距离是待排数组长度除以1.3得到近似值,下次则以上次得到的近似值再除以1.3,直到距离小至3时,以1递减
不太好描述,还是看例子吧
假设待数组[8 4 3 7 6 5 2 1]
待排数组长度为8,而8÷1.3=6,则比较8和2,4和1,并做交换
[8 4 3 7 6 5 2 1]
[8 4 3 7 6 5 2 1]
交换后的结果为
[2 1 3 7 6 5 8 4]
第二次循环,更新间距为6÷1.3=4,比较2和6,1和5,3和8,7和4
[2 1 3 7 6 5 8 4]
[2 1 3 7 6 5 8 4]
[2 1 3 7 6 5 8 4]
[2 1 3 7 6 5 8 4]
只有7和4需要交换,交换后的结果为
[2 1 3 4 6 5 8 7]
第三次循环,更新距离为3,没有交换
第四次循环,更新距离为2,没有交换
第五次循环,更新距离为1,三处交换
[2 1 3 4 6 5 8 7]
[2 1 3 4 6 5 8 7]
[2 1 3 4 6 5 8 7]
三处交换后的结果为[1 2 3 4 5 6 7 8]
交换后排序结束,顺序输出即可得到[1 2 3 4 5 6 7 8]
实现:
1 void comb_sort(int *data,int len) 2 { 3 const double shrink = 1.25; 4 int i,delta = len,noswap = 0; 5 while( !noswap ) 6 { 7 for(noswap = 1,i = 0; i +delta < len; i ++) 8 if(data[i] > data[i+delta]) 9 { 10 data[i] ^= data[i+delta]; 11 data[i+delta] ^= data[i]; 12 data[i] ^= data[i+delta]; 13 noswap = 0; 14 } 15 if(delta>1) 16 { 17 delta /= shrink; 18 noswap = 0; 19 } 20 } 21 }
15,耐心排序 -- Patience Sort
这个排序的关键在建桶和入桶规则上
建桶规则:如果没有桶,新建一个桶;如果不符合入桶规则那么新建一个桶
入桶规则:只要比桶里最上边的数字小即可入桶,如果有多个桶可入,那么按照从左到右的顺序入桶即可
举个例子,待排数组[6 4 5 1 8 7 2 3]
第一步,取数字6出来,此时一个桶没有,根据建桶规则1新建桶,将把自己放进去,为了表述方便该桶命名为桶1或者1号桶
第二步,取数字4出来,由于4符合桶1的入桶规则,所以入桶1,并放置在6上边,如下图2所示
第三步,取数字5出来,由于5不符合桶1的入桶规则,比桶1里最上边的数字大,此时又没有其它桶,那么根据建桶规则新建桶2,放入住该桶
第四步,取数字1出来,1即符合入1号桶的规则,比4小嘛,也符合入2号桶的规则,比5也小,两个都可以入,根据入桶规则1入住1号桶(实际入住2号桶也没关系)
第五步,取数字8出来,8比1号桶的掌门1大,比2号桶的掌门5也大,而且就这俩桶,所以8决定自立门派,建立了3号桶,并入住该桶成为首位掌门
第六步,取数字7出来,1号桶,2号桶的掌门都不行,最后被3号桶收服,投奔了3号桶的门下
第七步,取数字2出来,被2号桶掌门收了
第八步,取数字3出来,被3号桶的现任掌门7收了
全部入桶完毕....

然后从第一个桶顺序取出数字1 4 6,2 5,3 7 8
剩下的使用插入排序结束战斗
伪代码:
1 BOOL PatienceSort(datatype *array, int size) 2 { 3 int i, j; 4 Node **bucket; 5 Node *p; 6 7 if(array == NULL) { 8 return FALSE; 9 } 10 11 bucket = (Node **)calloc(size, sizeof(Node *)); 12 if(bucket == NULL) { 13 return FALSE; 14 } 15 16 for(i = 0; i < size; i++) { 17 j = 0; 18 //找到第一个最上面的数据比关键字大的桶,如果没找到则指向一个空位置 19 while(bucket[j] != NULL && (bucket[j])->data < array[i]) 20 j++; 21 22 p = (Node *)malloc(sizeof(Node)); 23 if(p == NULL) { 24 return FALSE; 25 } 26 p->data = array[i]; 27 //将关键字入桶 28 if(bucket[j] != NULL) { 29 p->next = bucket[j]; 30 } else { 31 p->next = NULL; 32 } 33 34 bucket[j] = p; 35 } 36 i = j = 0; 37 //顺序的从第一个桶到最后一个桶中取出数据 38 while(bucket[j] != NULL) { 39 p = bucket[j]; 40 while(p != NULL) { 41 array[i++] = p->data; 42 p = p->next; 43 } 44 j++; 45 } 46 //进行一次插入排序 47 InsertionSort(array, size); 48 49 return TRUE; 50 }
16,珠排序 -- Bead Sort
珠排序非常另类[地精也很另类],看完你就知道了,先介绍思路,再分解过程
英文论文地址:http://www.cs.auckland.ac.nz/~jaru003/research/publications/journals/beadsort.pdf
先了解一个概念,不然不容易理解,一个数字3用3个1来表示
一个数字9用9个1来表示,珠排序中的珠指的是每一个1,它把每一个1想像成一个珠子,这些珠子被串在一起,想像下算盘和糖葫芦

上图中的三个珠就表示数字3,两个珠表示数字2,这个OK了继续,这里的3和2都叫bead

上图(a)中有两个数字,4和3,分别串在四条线上,于是数字4的最后一个珠子下落,因为它下边是空的,自由下落后变成图(b)
图(c)中随机给了四个数字,分别是3,2,4,2,这些珠子自由下落,就变成了(d)中,落完就有序了,2,2,3,4
以上就是珠排序的精华

上图中的n表示待排序数组的长度,有多少数字就有多少层,横向表示一层
m表示有多少个珠子,就是多少个1,这取决于最大数是几
比如待排数组[6 2 4 1 5 9]

让珠子全部做自由落体运动
9没有什么好落的,它在最底层
5也没有什么好落的,全部有支撑点
1同样不需要滑落
4除了第一个珠子不动外,其它三颗全部下落,落到1的位置变成下边这样

过程的细节不画了,原则就是你下边有支点,你就不用再滑落了,最后变成下边这样,排序完毕

从上到下顺序输出即可得到结果:[ 1 2 4 5 6 9]
实现样例:
1 #include <iostream> 2 #include <malloc.h> 3 4 using namespace std; 5 6 int GetMax(int *array,int size,int &len) 7 { 8 len = -1; 9 for( int i = 0; i < size; i ++ ) if( array[i] > len ) len = array[i]; 10 } 11 12 void BeadSort(int *array, int size) 13 { 14 char **bead; 15 int i,j,k,n,len; 16 if( !array ) return ; 17 18 //确定每行珠子的最大个数 19 GetMax(array,size,len); 20 cout << "Max Len of This Array is : " << len << endl; 21 //初始化 22 bead = (char **)calloc(size,sizeof(char *)); 23 if( !bead ) return ; 24 for( i = 0; i < size; i ++ ) 25 { 26 bead[i] = (char*)calloc(len,sizeof(char)); 27 if(!bead[i]) return ; 28 } 29 for( i = 0 ;i < size; i ++ ) for(j = 0; j < array[i]; j ++) bead[i][j] = 1; 30 //初始化完毕,将所有的数按顺序用珠子表示。 31 32 //让珠子自由下落 33 for(j = 0; j < len; j ++ ) 34 { 35 i = k = size - 1; 36 while(i >= 0 ) if( bead[i--][j] == 1 ) bead[k--][j] = 1; 37 while( k >= 0 ) bead[k--][j] = 0; 38 } 39 //自由下落完毕 40 41 //收集珠子,统计每一行有多少个珠子 42 for( i = 0; i < size; i ++ ) 43 { 44 j = n = 0; 45 while( i < len ) 46 { 47 if( !bead[i][j++]) break; 48 n ++; 49 } 50 array[i] = n; 51 } 52 } 53 54 int main() 55 { 56 int array[] = {9,11,15,20,19,0,5,1,10,17,13,15,11,19,11,7,20,6,10}; 57 int i=0,len = sizeof(array)/sizeof(int); 58 cout << "Before Sort: " ; 59 for( i = 0 ; i < len ; i ++ ) 60 cout << array[i] << " "; 61 cout << endl; 62 BeadSort(array,sizeof(array)/sizeof(int)); 63 64 cout << "After Sort: " ; 65 for( i = 0 ; i < len ; i ++ ) 66 cout << array[i] << " "; 67 cout << endl; 68 69 return 0; 70 }
结果:

复杂度:
珠排序可以是以下复杂度级别:
O(1):即所有珠子都同时移动,但这种算法只是概念上的,无法在计算机中实现
O(√n):在真实的物理世界中用引力实现,所需时间正比于珠子最大高度的平方根,而最大高度正比于n
O(n):一次移动一列珠子,可以用模拟和数字的硬件实现。
O(S),S是所有输入数据的和:一次移动一个珠子,能在软件中实现
17,计数排序 -- Counting sort
计数排序的过程类似小学选班干部的过程 ,如某某人10票,某人9票,那某某人是班长,某人是副班长
大体上分两个部分: 第一部分是拉选票和投票 , 第二部分是根据票数入桶
看具体过程,一共需要三个数据组,分别是: 待排序数组,票箱数组 和 桶数组
int * unsorted = new int[N]; //{ 6,2,4,1,5,9}; //待排数组
int * ballot = new int[N]; //票箱数组
int * bucket = new int[N]; //桶数组
最后再看桶数组,先看待排数组和票箱数组
初始状态,迭代变量 i = 0 时,待排序数组[i] = 6,票箱数组[i] = 0, 这样通过迭代变量建立了数字与其桶号(即票数)的联系
待排数组[ 6 2 4 1 5 9 ] i = 0时,可以从待排数组中取出6
票箱数组[ 0 0 0 0 0 0 ] 同时可以从票箱数组里取出6的票数0,即桶号
拉选票的过程:
首先6出列开始拉选票,6的票箱是0号,6对其它所有数字说,谁比我小或与我相等,就给我投票,不然揍你
于是,2 4 1 5 分别给6投票,放入0号票箱,6得四票
票箱数组[ 4 0 0 0 0 0 ]
接下来2开始拉选票,对其它人说,谁比我小,谁投我票,不然弄你!于是1投了一票,其他人比2大不搭理,心想你可真二。于是2从1那得到一票
待排数组[ 6 2 4 1 5 9 ]
票箱数组[ 4 1 0 0 0 0 ]
再然后是,4得到2和1的投票,共计两票。
1得到0票,没人投他
5得到2,4,1投的三张票
9是最大,得到所有人(自己除外)的投票,共计5票(数组长度-1票)
投票完毕时的状态是这样
待排数组[ 6 2 4 1 5 9 ]
票箱数组[ 4 1 2 0 3 5 ]
入桶的过程:
投票过程结束,每人都拥有自己的票数,桶数组说,看好你自己的票数,进入与你票数相等的桶,GO
6共计4票,进入4号桶
2得1票,进入1号桶,有几票就进几号桶
4两票,进2号桶,5三票进3号桶,9有5票,进5号桶
待排数组[ 6 2 4 1 5 9 ]
票箱数组[ 4 1 2 0 3 5 ]
-----------------------
入桶前 [ 0 1 2 3 4 5 ] //里边的数字表示桶编号
入桶后 [ 1 2 4 5 6 9 ] //1有0票,进的0号桶
排序完毕,顺序输出即可[ 1 2 4 5 6 9]
可以看到,数字越大票数越多,9得到除自己外的所有人的票,5票,票数最多所以9最大,
每个人最多拥有[数组长度减去自己]张票
1票数最少,所以1是最小的数,
样例实现:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #define random(x) rand()%(x) 4 #define NUM 100//产生100个随机数 5 #define MAXNUM 200//待排序的数字范围是0-200 6 void countingSort(int A[], int n, int k){ 7 int *ptemp, *pout; 8 int i; 9 ptemp = (int *)malloc(sizeof(int)*k); 10 pout = (int *)malloc(sizeof(int)*n); 11 for (i = 0; i < k; i++) 12 ptemp[i] = 0; 13 for (i = 0; i < n; i++) 14 ptemp[A[i]] += 1; 15 for (i = 1; i < k; i++) 16 ptemp[i] = ptemp[i - 1] + ptemp[i]; 17 for (i = n - 1; i >= 0; i--) 18 { 19 pout[ptemp[A[i]] - 1] = A[i]; 20 ptemp[A[i]] -= 1; 21 } 22 for (i = 0; i < n; i++) 23 A[i] = pout[i]; 24 free(ptemp); 25 free(pout); 26 } 27 void printArray(int A[], int n){ 28 int i = 0; 29 for (i = 0; i < n; i++){ 30 printf("%4d", A[i]); 31 } 32 printf("\n"); 33 } 34 35 void main() 36 { 37 int A[NUM]; 38 int i; 39 for (i = 0; i < NUM; i++) 40 A[i] = random(MAXNUM); 41 printf("before sorting:\n"); 42 printArray(A, NUM); 43 countingSort(A, NUM, MAXNUM); 44 printf("after sorting:\n"); 45 printArray(A, NUM); 46 } 47
先回忆下桶排序是怎么回事,它与桶的区别在于入桶规则,桶排序里是1入1号桶,2入2号桶
这个排序把数字分区了,然后给出一个所谓的键,例如它规定0-9都入0号桶
10-19都入1号桶,这样桶覆盖的范围将增大10倍,这在某种情况下是很有用的
有了桶排的基础后,再看下边两张图就什么都明白了,不再分解过程了


以下参考:http://dsqiu.iteye.com/blog/1707383
Proxmap Sort是桶排序和基数排序的改进。ProxMap的排序采用不同的方法来排序,这在概念上是类似哈希。该算法使用桶技术对哈希方法进行改变,桶的大小不相同。
Array table
| A1 | 6.7 | 5.9 | 8.4 | 1.2 | 7.3 | 3.7 | 11.5 | 1.1 | 4.8 | 0.4 | 10.5 | 6.1 | 1.8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | 1 | 3 | 0 | 1 | 1 | 1 | 2 | 1 | 1 | 0 | 1 | 1 | |
| P | 0 | 1 | -9 | 4 | 5 | 6 | 7 | 9 | 10 | -9 | 11 | 12 | |
| L | 7 | 6 | 10 | 1 | 9 | 4 | 12 | 1 | 5 | 0 | 11 | 7 | 1 |
| A2 | 0.4 | 1.1 | 1.2 | 1.8 | 3.7 | 4.8 | 5.9 | 6.1 | 6.7 | 7.3 | 8.4 | 10.5 | 11.5 |

Technique:
1, Create 4 arrays and initialize
- int HitList[ARRAYSIZE] -- Keeps a count of the number of hits at each index in the sorted array. HitList[x] holds a count of the number of items whose keys hashed to x. Initialize to all 0.
- int Location[ARRAYSIZE] -- Indices in the sorted array calculated using the hash function. Item x in the unsorted array has its hash index stored in Location[x]. Does not need to be initialized.
- int ProxMap[ARRAYSIZE] -- Starting index in the sorted array for each bucket. If HitList[x] is not 0 then ProxMap[x] contains the starting index for the bucket of keys hashing to x. Initialize to all keys to -1 (unused).
- StructType DataArray2[ARRAYSIZE] -- Array to hold the sorted array. Initialize to all -1 (unused).
2,Use the keys of the unsorted array and a carefully chosen hash function to generate the indices into the sorted array and save these. The hash function must compute indices always in ascending order. Store each hash index in the Location[] array. Location[i] will hold the calculated hash index for the ith structure in the unsorted array.
HIdx = Hash(DataArray[i]);
Location[i] = HIdx;
Care must be taken in selecting the hash function so that the keys are mapped to the entire range of indexes in the array. A good approach is to convert the keys to integer values if they are strings, then map all keys to floats in the range 0<= Key < 1. Finally, map these floats to the array indices using the following formulas:
/* Map all integer keys to floats in range 0<= Key < 1 */
KeyFloat = KeyInt / (1 + MAXKEYINTVALUE);
/* Map all float keys to indices in range 0<= Index < ARRAYSIZE */
Index = floor(ARRAYSIZE * KeyFloat);
This will then produce indices insuring that all the keys are kept in ascending order (hashs computed using a mod operator will not.)
3,Keep a count of the number of hits at each hash index. HitList[Hidx]++
4,Create the ProxMap (short for proximity map) from the hit list giving the starting index in the sorted array for each bucket.
RunningTotal = 0; /* Init counter */
for(i=0; i 0) /* There were hits at this address */
{
ProxMap[i] = RunningTotal; /* Set start index for this set */
RunningTotal += HitList[i];
}
}
5,Move keys from the unsorted array to the sorted array using an insertion sort technique for each bucket.

In this diagram 5 sets of structures are sorted when delta = 5
Analysis: ProxMap sorting runs in a surprisingly fast O(n) time.
C代码:
1 /******************************************************/ 2 /* ProxmapSort.c */ 3 /* */ 4 /* Proxmap sort demonstration. */ 5 /* Author: Rick Coleman */ 6 /* Date: April 1998 */ 7 /******************************************************/ 8 #include <stdio.h> 9 #include <conio.h> 10 #include "sort.h" 11 #include <math.h> 12 13 #define ARRAYSIZE 32 14 15 /* Prototype sort function */ 16 void ProxmapSort(StructType DataArray[], StructType DataArray2[],int count); 17 int Hash(int key, int KeyMax, int KeyMin, int count); 18 void ProxMapInsertionSort(StructType DataArray[], StructType *theStruct, 19 int startIdx, int listLen); 20 21 int main(void) 22 { 23 StructType DataArray[32], DataArray2[32]; 24 int count; 25 26 count = ReadRecords(DataArray, 32); 27 printf("Unsorted list of records.\n\n"); 28 PrintList(DataArray, count); 29 30 ProxmapSort(DataArray, DataArray2, count); 31 32 printf("Sorted list of records.\n\n"); 33 PrintList(DataArray2, count); 34 printf("Sorting done...\n"); 35 getch(); 36 return(0); 37 } 38 39 40 /***************************************/ 41 /* ProxmapSort() */ 42 /* */ 43 /* Sort records on integer key using */ 44 /* a proxmap sort. */ 45 /***************************************/ 46 void ProxmapSort(StructType DataArray[], StructType DataArray2[],int count) 47 { 48 int i; 49 int HitList[ARRAYSIZE]; 50 int Hidx; /* Hashed index */ 51 int ProxMap[ARRAYSIZE]; 52 int RunningTotal; /* Number of hits */ 53 int Location[ARRAYSIZE]; 54 int KeyMax, KeyMin; /* Used in Hash() */ 55 56 /* Initialize hit list and proxmap */ 57 for(i=0; i<count; i++) 58 { 59 HitList[i] = 0; /* Init to all 0 hits */ 60 ProxMap[i] = -1; /* Init to all unused */ 61 DataArray2[i].key = -1; /* Init to all empty */ 62 } 63 64 /* Find the largest key for use in computing the hash */ 65 KeyMax = 0; /* Guaranteed to be less than the smallest key */ 66 KeyMin = 32767; /* Guaranteed to be more than the largest key */ 67 for(i=0; i<count; i++) 68 { 69 if(DataArray[i].key > KeyMax) KeyMax = DataArray[i].key; 70 if(DataArray[i].key < KeyMin) KeyMin = DataArray[i].key; 71 } 72 73 /* Compute the hit count list (note this is not a collision count, but 74 a collision count+1 */ 75 for(i=0; i<count; i++) 76 { 77 Hidx = Hash(DataArray[i].key, KeyMax, KeyMin, count); /* Calculate hash index */ 78 Location[i] = Hidx; /* Save this for later. (Step 1) */ 79 HitList[Hidx]++; /* Update the hit count (Step 2) */ 80 } 81 82 /* Create the proxmap from the hit list. (Step 3) */ 83 RunningTotal = 0; /* Init counter */ 84 for(i=0; i<count; i++) 85 { 86 if(HitList[i] > 0) /* There were hits at this address */ 87 { 88 ProxMap[i] = RunningTotal; /* Set start index for this set */ 89 RunningTotal += HitList[i]; 90 } 91 } 92 93 // NOTE: UNCOMMENT THE FOLLOWING SECTION TO SEE WHAT IS IN THE ARRAYS, BUT 94 // COMMENT IT OUT WHEN DOING A TEST RUN AS PRINTING IS VERY SLOW AND 95 // WILL RESULT IN AN INACCURATE TIME FOR PROXMAP SORT. 96 /* ---------------------------------------------------- 97 // Print HitList[] to see what it looks like 98 printf("HitList:\n"); 99 for(i=0; i<count; i++) 100 printf("%d ", HitList[i]); 101 printf("\n\n"); 102 getch(); 103 104 // Print ProxMap[] to see what it looks like 105 printf("ProxMap:\n"); 106 for(i=0; i<count; i++) 107 printf("%d ", ProxMap[i]); 108 printf("\n\n"); 109 getch(); 110 111 // Print Location[] to see what it looks like 112 printf("Location:\n"); 113 for(i=0; i<count; i++) 114 printf("%d ", Location[i]); 115 printf("\n\n"); 116 getch(); 117 --------------------------------------------- */ 118 119 /* Move the keys from A1 to A2 */ 120 /* Assumes A2 has been initialized to all empty slots (key = -1)*/ 121 for(i=0; i<count; i++) 122 { 123 if((DataArray2[ProxMap[Location[i]]].key == -1)) /* If the location in A2 is empty...*/ 124 { 125 /* Move the structure into the sorted array */ 126 DataArray2[ProxMap[Location[i]]] = DataArray[i]; 127 } 128 else /* Insert the structure using an insertion sort */ 129 { 130 ProxMapInsertionSort(DataArray2, &DataArray[i], ProxMap[Location[i]], HitList[Location[i]]); 131 } 132 } 133 134 } 135 136 /***************************************/ 137 /* Hash() */ 138 /* */ 139 /* Calculate a hash index. */ 140 /***************************************/ 141 int Hash(int key, int KeyMax, int KeyMin, int count) 142 { 143 float keyFloat; 144 145 /* Map integer key to float in the range 0 <= key < 1 */ 146 keyFloat = (float)(key - KeyMin) / (float)(1 + KeyMax - KeyMin); 147 148 /* Map float key to indices in range 0 <= index < count */ 149 return((int)floor(count * keyFloat)); 150 } 151 152 /***************************************/ 153 /* ProxMapInsertionSort() */ 154 /* */ 155 /* Use insertion sort to insert a */ 156 /* struct into a subarray. */ 157 /***************************************/ 158 void ProxMapInsertionSort(StructType DataArray[], StructType *theStruct, 159 int startIdx, int listLen) 160 { 161 /* Args: DataArray - Partly sorted array 162 *theStruct - Structure to insert 163 startIdx - Index of start of subarray 164 listLen - Number of items in the subarray */ 165 int i; 166 167 /* Find the end of the subarray */ 168 i = startIdx + listLen - 1; 169 while(DataArray[i-1].key == -1) i--; 170 171 /* Find the location to insert the key */ 172 while((DataArray[i-1].key > theStruct->key) && (i > startIdx)) 173 { 174 DataArray[i] = DataArray[i-1]; 175 i--; 176 } 177 178 /* Insert the key */ 179 DataArray[i] = *theStruct; 180 }
算法wiki: https://en.wikipedia.org/wiki/Proxmap_sort
19,Flash Sort
FlashSort依然类似桶排,主要改进了对要使用的桶的预测,或者说,减少了无用桶的数量从而节省了空间,例如
待排数字[ 6 2 4 1 5 9 100 ]桶排需要100个桶,而flash sort则由于可以预测桶则只需要7个桶
即待排数组长度个桶,如何预测将要使用的桶有这么一个公式

该排序有前置条件,需要知道待排数组的区间和待排数组的长度,
例如已知待排数组[ 6 2 4 1 5 9 ]的长度为6,最大值9,最小值1,这三个是已知条件,如果无法知道这三个则无法应用该排序
预测的思想:
如果有这样一个待排数组,其最大值是100,最小值是1,数组长度为100,那么50在排完序后极有可能出现在正中间,flash sort就是基于这个思路
预测桶号细节:
待排数组[ 6 2 4 1 5 9 ]
具体看6可能出现的桶号
Ai - Amin 是 6 - 1 = 5
Amax - Amin 是9 - 1 = 8
m - 1 是数组长度6 - 1 = 5
则(m - 1) * (Ai - Amin) / (Amax - Amin) = 5 * 5 / 8 =25/8 = 3.125
最后加上1等于 4.125
6预测的桶号为4.125
2预测的桶号为1.625
4预测的桶号为2.875
1预测的桶号为1
5预测的桶号为3.5
9预测的桶号为5
去掉小数位后,每个数字都拥有自己预测的桶号,对应如下所示
待排数组[ 6 2 4 1 5 9 ]
预测桶号[ 4 1 2 1 3 5 ]
入桶规则:
1号桶 2,1
2号桶 4
3号桶 5
4号桶 6
5号桶 9
1号桶内两个数字使用任意排序算法使之有序,其它桶如果此种情况同样需要在桶内排序,使用什么排序算法不重要,重要的是排成从小到大即可
最后顺序从桶里取出来即可
[1 2 4 5 6 9]
wiki 地址: https://en.wikipedia.org/wiki/Flashsort
20,Strand Sort
Strand sort是思路是这样的,它首先需要一个空的数组用来存放最终的输出结果,给它取个名字叫"有序数组"
然后每次遍历待排数组,得到一个"子有序数组",然后将"子有序数组"与"有序数组"合并排序
重复上述操作直到待排数组为空结束
例子:
待排数组[ 6 2 4 1 5 9 ]
第一趟遍历得到"子有序数组"[ 6 9],并将其归并排序到有序数组里
待排数组[ 2 4 1 5]
有序数组[ 6 9 ]
第二趟遍历再次得到"子有序数组"[2 4 5],将其归并排序到有序数组里
待排数组[ 1 ]
有序数组[ 2 4 5 6 9 ]
第三趟遍历再次得到"子有序数组"[ 1 ],将其归并排序到有序数组里
待排数组[ ... ]
有序数组[ 1 2 4 5 6 9 ]
待排数组为空,排序结束
代码参考地址:http://blog.csdn.net/tiantangrenjian/article/details/7172942
#include <iostream> using namespace std; void merge(int res[],int resLen,int sublist[],int last) { int *temp = (int *)malloc(sizeof(int)*(resLen+last)); int beginRes=0; int beginSublist=0; int k; for(k=0;beginRes<resLen && beginSublist<last;k++) { if(res[beginRes]<sublist[beginSublist]) temp[k]=res[beginRes++]; else temp[k]=sublist[beginSublist++]; //cout<<"k:"<<k<<" temp[k]:"<<temp[k]<<endl; } if(beginRes<resLen) memcpy(temp+k,res+beginRes,(resLen-beginRes)*sizeof(int)); else if(beginSublist<last) memcpy(temp+k,sublist+beginSublist,(last-beginSublist)*sizeof(int)); memcpy(res,temp,(resLen+last)*sizeof(int)); free(temp); } void strandSort(int array[],int length) { int *sublist=(int *)malloc(sizeof(int)*length); int *res=(int *)malloc(sizeof(int)*length); //sizeof(array)=4 int i; int resLen=0; res[0]=array[0]; array[0]=0; for(i=1;i<length;i++) { if(array[i]>res[resLen]) { resLen++; res[resLen]=array[i]; array[i]=0; } } resLen++; int last; int times=1; bool finished; while (true) { finished = true; last = -1; for(i=times;i<length;i++) { //cout<<"This time array[i]: "<<array[i]<<endl; if(array[i]!=0) { //cout<<"This time array[i]: "<<array[i]<<endl; if (last==-1) { sublist[0]=array[i]; array[i]=0; last=0; finished = false; } else if(array[i]>sublist[last]) { last++; sublist[last]=array[i]; array[i]=0; } } } if(finished) break; last++; merge(res,resLen,sublist,last); resLen=resLen+last; times++; } memcpy(array,res,length*sizeof(int)); } int main() { //int array[]={15,9,8,1,4,11,7,2,13,16,5,3,6,2,10,14}; int array[]={13,14,94,33,82,25,59,94,65,23,45,27,73,25,39,10,35,54,90,58}; int i; int length=sizeof(array)/sizeof(int); //在这里 sizeof(array)=80 strandSort(array,length); //int *arr = array; //cout<<arr[2]<<endl; for(i=0;i<length;i++) { cout<<array[i]<<" "; } cout<<endl; return 0; }
21,圈排序 -- Cycle Sort
Cycle sort的思想与计数排序太像了,理解了基数排序再看这个会有很大的帮助,
圈排序与计数排序的区别在于圈排序只给那些需要计数的数字计数,先看完文章吧,看完再回来理解这一句话
所谓的圈的定义,我只能想到用例子来说明,实在不好描述
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第一部分
第一步,我们现在来观察待排数组和排完后的结果,以及待排数组的索引,可以发现
排完序后的6应该出现在索引4的位置上,而它现在却在位置0上,
记住这个位置啊,一直找到某个数应该待在位置0上我们的任务就完成了
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第二步,而待排数组索引4位置上的5应该出现在索引3的位置上
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第三步,同样的,待排数组索引3的位置是1,1应该出现在位置0上,注意注意,找到这么一个数了:1,它应该待在位置0上
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第四步,而索引0处却放着6,而6应该出现在索引4的位置,至此可以发现,回到原点了,问题回到第一步了,
所以这里并不存在所谓的第四步,前三步就已经转完一圈了
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
这就是所谓的一圈!真不好描述,不知道您看明白没...汗.
前三步转完一圈,得到的数据分别是[ 6 5 1 ]
第二部分
第一步,圈排序并不是一圈排序,而一圈或多圈排序,所以,还得继续找,这一步从第二个数字2处开始转圈
待排中的2位于索引1处,排序完毕仍然处于位置1位置,所以这一圈完毕,得到圈数据[ 2 ]
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第三部分
第一步,同上,4也出现了它应该待的位置,结束这一圈,得到第三个圈:[ 4 ]
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
第四部分
第一步,由于1和5出现在第一圈里,这是什么意思呢,说明这两个数已经有自己的圈子了,不用再找了,
即是找,最后还是得到第一圈的数据[ 6 5 1 ],所以,1和5跳过,这一部分实际应该找的是9,来看看9的圈子
9应该出现在索引5的位置,实际上它就在索引5的位置,与第二部分的第一步的情况一样,所以这一圈的数据也出来了:[ 9 ]
待排数组[ 6 2 4 1 5 9 ]
排完序后[ 1 2 4 5 6 9 ]
数组索引[ 0 1 2 3 4 5 ]
一共找到四个圈子,分别是
[ 6 5 1 ] , [ 2 ] ,[ 4 ] , [ 9 ]
如果一个圈只有一个数字,那么它是不需要转圈的,即不需要排序,那么只有第一个圈排序即可
你可能要问了,前边的那些圈子都是基于已知排序结果才能得到,我都已知结果还排个毛啊
以上内容都是为了说明什么是圈,知道什么是圈后才能很好的理解圈排序
现在来分解排序的细节
第一步,将6取出来,计算出有4个数字比6小,将6放入索引4,同时原索引4位置的数字5出列
排序之前[ 0 2 4 1 5 9 ] 6
排序之后[ 0 2 4 1 6 9 ] 5
索引位置[ 0 1 2 3 4 5 ]
第二步,当前数字5,计算出有3个数字比5小,将5放入索引3,同时原索引3位置的数字
排序之前[ 0 2 4 1 6 9 ] 5
排序之后[ 0 2 4 5 6 9 ] 1
索引位置[ 0 1 2 3 4 5 ]
第三步,当前数字1,计算出有0个数字比1小,将1放入索引0,索引0处为空,这圈完毕
排序之前[ 0 2 4 5 6 9 ] 1
排序之后[ 1 2 4 5 6 9 ]
索引位置[ 0 1 2 3 4 5 ]
第一个圈[ 6 5 1 ]完毕
第四步,取出下一个数字2,计算出有1个数字比2小,将2放入索引1处,发现它本来就在索引1处
第五步,取出下一个数字4,计算出有2个数字比4小,将4放入索引2处,发现它本来就在索引2处
第六步,取出下一个数字5,5在第一个圈内,不必排序
第七步,取出下一个数字6,6在第一个圈内,不必排序
第八步,取出下一个数字9,计算出有5个数字比9小,将9放入索引5处,发现它本来就在索引5处
全部排序完毕
wiki 地址: https://en.wikipedia.org/wiki/Cycle_sort
22, 图书馆排序 -- Library sort
思路简介,大概意思是说,排列图书时,如果在每本书之间留一定的空隙,那么在进行插入时就有可能会少移动一些书,说白了就是在插入排序的基础上,给书与书之间留一定的空隙,这个空隙越大,需要移动的书就越少,这是它的思路,用空间换时间
看红线标的那句话知道,这个空隙留多大,你自己定
图书馆排序的关键是分配空间,分配完空间后直接使用插入排序即可

进行空间分配的过程
这个我实在是找不到相关的资料,没准就是平均分配嘞
进行插入排序的过程
举例待排数组[ 0 0 6 0 0 2 0 0 4 0 0 1 0 0 5 0 0 9 ],直接对它进行插入排序
第一次移动,直接把2放6前边
[ 0 2 6 0 0 0 0 0 4 0 0 1 0 0 5 0 0 9 ]
第二次移动,先把6往后挪,然后把4放在刚才6的位置,移动了一个位置
[ 0 2 4 6 0 0 0 0 0 0 0 1 0 0 5 0 0 9 ]
第三次移动,直接把1放2前边
[ 1 2 4 6 0 0 0 0 0 0 0 0 0 0 5 0 0 9 ]
第四次移动,再把6往后挪一位,把5放在刚才6的位置
[ 1 2 4 5 6 0 0 0 0 0 0 0 0 0 0 0 0 9 ]
第五次移动后,把9放6后边,排序结束
[ 1 2 4 5 6 9 0 0 0 0 0 0 0 0 0 0 0 0 ]
以上算法总结自各个网站,出处都给出地址!转载请注明原出处
wiki 地址: https://en.wikipedia.org/wiki/Library_sort


 浙公网安备 33010602011771号
浙公网安备 33010602011771号