表达式转表达式二叉树
表达式树
二叉树是表达式处理的常用工具,例如,a+b*(c-d)-e/f可以表示成如下所示的二叉树
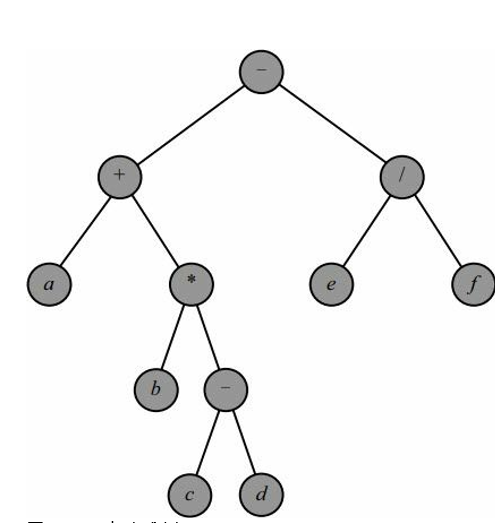
其中,每个非叶子节点表示一个运算符,左子树是第一个运算数对应的表达式,右子树是第二个表达式对应的表达式。每个叶子节点都是数。
其在空间利用上也非常高效,节点数等于表达式的长度。
表达式转二叉树
lrj说方法有很多种,下面介绍他讲的一种:找到“最后计算”的运算符(它是整个表达式树的根),然后递归处理左右两边。
1 const int maxn = 1000 + 10;
2 char str[maxn];
3 int lch[maxn + 1], rch[maxn + 1]; char op[maxn + 1]; //每个结点的左右子结点编号和字符
4 int nc = 0; //结点数
5 int build_tree(char* s, int x, int y)
6 {
7 int i, c1=-1, c2=-1, p=0;
8 int u;
9 if(y-x == 1) //仅一个字符,建立单独结点
10 {
11 u = ++nc;
12 lch[u] = rch[u] = 0;
13 op[u] = s[x];
14 return u;
15 }
16
17 for (i = x; i < y; i++) //寻找根节点的位置
18 {
19 switch (s[i])
20 {
21 case '(': p++; break;
22 case ')': p--; break;
23 case '+':
24 case '-': if (!p) c1 = i; break;
25 case '*':
26 case '/': if (!p) c2 = i; break;
27 }
28 }
29 if (c1 < 0) c1 = c2; //找不到括号外的加减号,就用乘除号
30 if(c1 < 0) return build_tree(s, x+1, y-1); //整个表达式被一对括号括起来
31 u = ++nc;
32 lch[u] = build_tree(s, x, c1);
33 rch[u] = build_tree(s, c1+1, y);
34 op[u] = s[c1];
35 return u;
36 }
前缀式、中缀式、后缀式
前缀表达式和后缀表达式分别对应表达式树前序和后序遍历的结果,如果不考虑括号,中缀表达式对应表达式树中序遍历的结果。
1 //中序遍历
2 void InOrder(int root)
3 {
4 if (lch[root] > 0) InOrder(lch[root]);
5 printf("%c ", op[root]);
6 if (rch[root] > 0) InOrder(rch[root]);
7 }
8
9 //后序遍历
10 void PostOrder(int root)
11 {
12 if (lch[root] > 0) PostOrder(lch[root]);
13 if (rch[root] > 0) PostOrder(rch[root]);
14 printf("%c ", op[root]);
15 }
表达式求值
有了表达式树求值就非常简单了,先求左子树的值,再求右子树值,然后根据根节点的运算符计算最终的值。整个过程采用递归求解。
(注意!!这种方法只能求个位数表达式的值)
1 //根据表达式二叉树求值
2 int cal(int root)
3 {
4 int ans = 0;
5 char ch = op[root];
6 if (isdigit(ch)) return ch - '0';
7 switch (ch)
8 {
9 case '+': ans = cal(lch[root]) + cal(rch[root]); break;
10 case '-': ans = cal(lch[root]) - cal(rch[root]); break;
11 case '*': ans = cal(lch[root]) * cal(rch[root]); break;
12 case '/': ans = cal(lch[root]) / cal(rch[root]); break;
13 }
14 return ans;
15 }
打印二叉树(括号表达法)
root(lch,rch)像这样的格式,其中lch,rch本身也是这样的格式(递归定义)。整个过程类似于先序遍历,先打印根节点,再打印左子树,再打印右子树。
注意格式,如果缺少左、右子树用空格代替(如root( ,rch)),如果都没有,则括号也省掉。
//打印表达式二叉树
void PrintTree(int root)
{
int flag = 0; //标记是否有左右子树
printf("%c", op[root]);
if (lch[root] > 0) flag += 1;
if (rch[root] > 0) flag += 2;
if (flag == 0) return;
if (flag == 1) //只有左子树
{
printf("(");
PrintTree(lch[root]);
printf(", )");
}
if (flag == 2) //只有右子树
{
printf("( ,");
PrintTree(rch[root]);
printf(")");
}
if (flag == 3) //左右子树都有
{
printf("(");
PrintTree(lch[root]);
printf(",");
PrintTree(rch[root]);
printf(")");
}
}
最一个加一个认真写的 胡乱写的能实现嵌套括号、多位数相加减乘除的完整代码
1 #include<stdio.h>
2 #include<string>
3
4 const int maxn = 1000 + 10;
5 char expr[maxn]; //原表达式
6 int str[maxn]; //转换后的表达式
7 int lch[maxn + 1], rch[maxn + 1],op[maxn + 1]; //每个结点的左右子结点编号和字符
8 bool is_alpha1[maxn], is_alpha2[maxn]; //是否为操作符或括号,前者对s数组,后者对op数组
9 int nc = 0; //结点数
10 int cnt = 0; //转换后字符串的长度
11
12 // 把表达式exp转化成参数形式,并存到str中
13 void analyse(char* expr)
14 {
15 int len = strlen(expr);
16 int i = 0;
17 while(i < len)
18 {
19 if (!isdigit(expr[i]))
20 {
21 str[cnt] = expr[i++];
22 is_alpha1[cnt++] = true;
23 }
24 else
25 {
26 int tmp = 0;
27 while (isdigit(expr[i]))
28 {
29 tmp = tmp * 10 + expr[i] - '0';
30 i++;
31 }
32 str[cnt] = tmp;
33 is_alpha1[cnt++] = false;
34 }
35 }
36 }
37
38 //表达式转表达式树
39 int build_tree(int* s, int x, int y)
40 {
41 int i, c1=-1, c2=-1, p=0;
42 int u;
43 if(y-x == 1) //仅一个字符,建立单独结点
44 {
45 u = ++nc;
46 lch[u] = rch[u] = 0;
47 op[u] = s[x];
48 if (is_alpha1[x]) is_alpha2[u] = true;
49 return u;
50 }
51
52 for (i = x; i < y; i++) //寻找根节点的位置
53 {
54 if(s[i] == '(' && is_alpha1[i]) p++;
55 if(s[i] == ')' && is_alpha1[i]) p--;
56 if((s[i] == '+' || s[i] == '-') && is_alpha1[i]) if (!p) c1 = i;
57 if((s[i] == '*' || s[i] == '/') && is_alpha1[i]) if (!p) c2 = i;
58 }
59 if (c1 < 0) c1 = c2; //找不到括号外的加减号,就用乘除号
60 if(c1 < 0) return build_tree(s, x+1, y-1); //整个表达式被一对括号括起来
61 u = ++nc;
62 lch[u] = build_tree(s, x, c1);
63 rch[u] = build_tree(s, c1+1, y);
64 op[u] = s[c1];
65 if (is_alpha1[c1]) is_alpha2[u] = true;
66 return u;
67 }
68
69 //先序遍历
70 void PreOrder(int root)
71 {
72 if(!is_alpha2[root]) printf("%d ", op[root]);
73 else printf("%c ", op[root]);
74
75 if (lch[root] > 0) PreOrder(lch[root]);
76 if (rch[root] > 0) PreOrder(rch[root]);
77 }
78
79 //中序遍历
80 void InOrder(int root)
81 {
82 if (lch[root] > 0) InOrder(lch[root]);
83
84 if (!is_alpha2[root]) printf("%d ", op[root]);
85 else printf("%c ", op[root]);
86
87 if (rch[root] > 0) InOrder(rch[root]);
88 }
89
90 //后序遍历
91 void PostOrder(int root)
92 {
93 if (lch[root] > 0) PostOrder(lch[root]);
94 if (rch[root] > 0) PostOrder(rch[root]);
95
96 if (!is_alpha2[root]) printf("%d ", op[root]);
97 else printf("%c ", op[root]);
98 }
99
100 //根据表达式二叉树求值
101 int cal(int root)
102 {
103 int ans = 0;
104 int ch = op[root];
105 if (!is_alpha2[root]) return ch;
106 switch (ch)
107 {
108 case '+': ans = cal(lch[root]) + cal(rch[root]); break;
109 case '-': ans = cal(lch[root]) - cal(rch[root]); break;
110 case '*': ans = cal(lch[root]) * cal(rch[root]); break;
111 case '/': ans = cal(lch[root]) / cal(rch[root]); break;
112 }
113 return ans;
114 }
115
116 //打印表达式二叉树
117 void PrintTree(int root)
118 {
119 int flag = 0; //标记是否有左右子树
120 if (!is_alpha2[root]) printf("%d", op[root]);
121 else printf("%c", op[root]);
122
123 if (lch[root] > 0) flag += 1;
124 if (rch[root] > 0) flag += 2;
125 if (flag == 0) return;
126 if (flag == 1) //只有左子树
127 {
128 printf("(");
129 PrintTree(lch[root]);
130 printf(", )");
131 }
132 if (flag == 2) //只有右子树
133 {
134 printf("( ,");
135 PrintTree(rch[root]);
136 printf(")");
137 }
138 if (flag == 3) //左右子树都有
139 {
140 printf("(");
141 PrintTree(lch[root]);
142 printf(",");
143 PrintTree(rch[root]);
144 printf(")");
145 }
146 }
147
148 int main()
149 {
150 printf("表达式:");
151 scanf("%s", expr);
152
153 analyse(expr); //转化
154
155
156 build_tree(str, 0, cnt); //建树
157
158 int root = 1;
159 printf("先序遍历:"); PreOrder(root); printf("\n"); //三种遍历
160 printf("中序遍历:"); InOrder(root); printf("\n");
161 printf("后序遍历:"); PostOrder(root); printf("\n");
162
163 printf("表达式二叉树:"); PrintTree(root); printf("\n"); //打印表达式二叉树
164
165 int ans;
166 ans = cal(root); //表达式求值
167 printf("表达式值:%d\n", ans);
168
169 return 0;
170 }
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号