过河问题(图论方法)
农夫过河问题
问题描述
一个农夫带着一头狼、一头羊、一颗白菜过河。他面前只有一条船,只能容纳他和一件物品,只有农夫会划船。如果农夫不在场,狼会吃羊、羊会吃白菜,农夫在场则不会。求将所有物品运到对岸的方案。
解题思路
根据物品的位置定义状态,若在左岸记为1,右岸记为0,于是最终方案就是(1,1,1,1)-->(0,0,0,0)所经过的路径。
1、定义状态
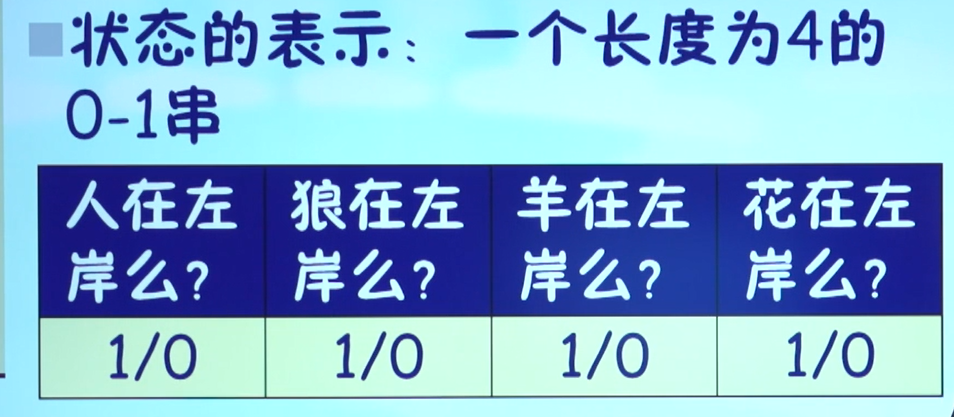
2、列举所有状态(人、狼、羊、菜)
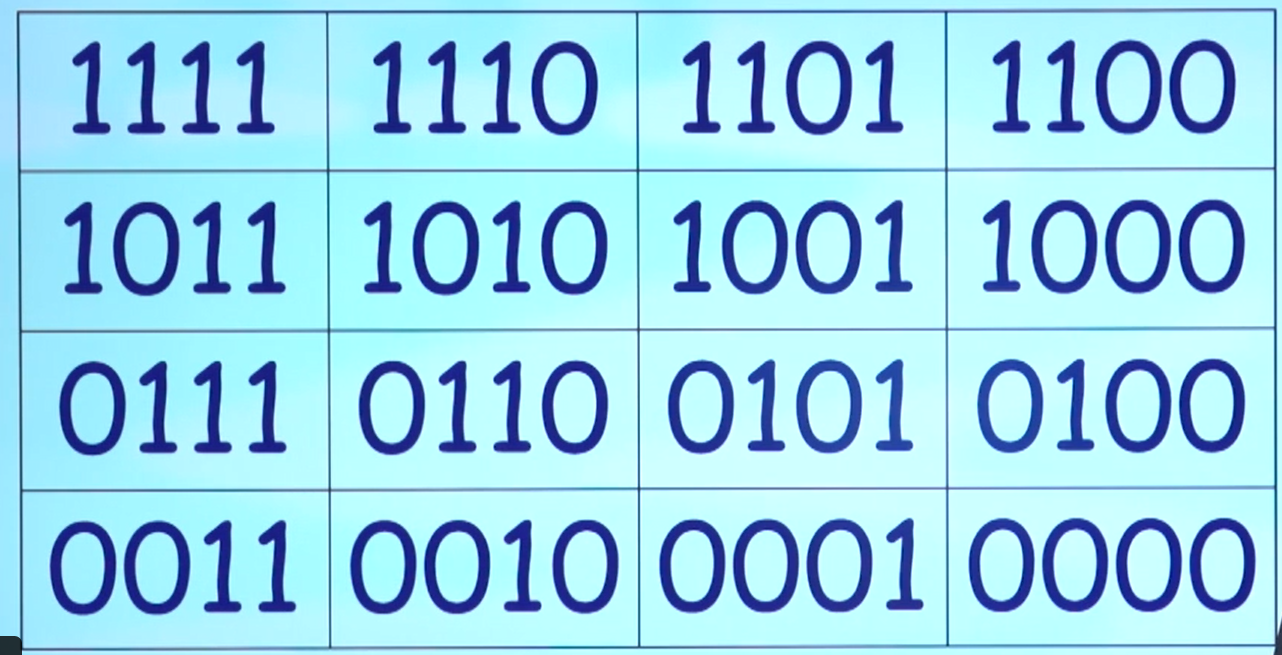
3、删除不合理的状态(狼和羊、羊和菜)

4、连边(模拟一次渡河)

5、寻找路径
寻找(1111)-->(0000)的边,可以用寻路算法如bfs、dfs,如果要求最短路可以用最短路算法如bfs、Dijsktra等,当然这里图很简单,可直接观察出来。
(1111)-->(0101)-->(1101)-->(0001)-->(1011)-->(0010)-->(1010)-->(0000)(两条最短路之一)
左岸 右岸
1、人 狼 羊 花 空
2、狼 花 人 羊
3、人 狼 花 羊
4、花 人 狼 羊
5、人 羊 花 狼
6、羊 人 花 狼
7、人 羊 狼 花
8、空 狼 花 人 羊
传教士与吃人恶魔的问题
问题描述
有三个传教士和三个吃人恶魔要渡过一条河,河中有一条船,只能装下两个人。在任何地方(无论是岸边还是船上),如果吃人恶魔数量多于传教士数量,吃人恶魔就会吃掉传教士。问:怎么才能让这些都安全过河?
解题思路
1、定义状态
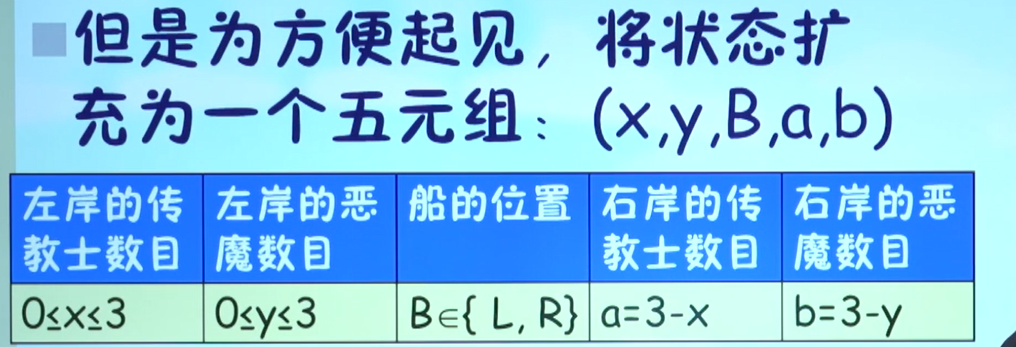
2、列举所有状态
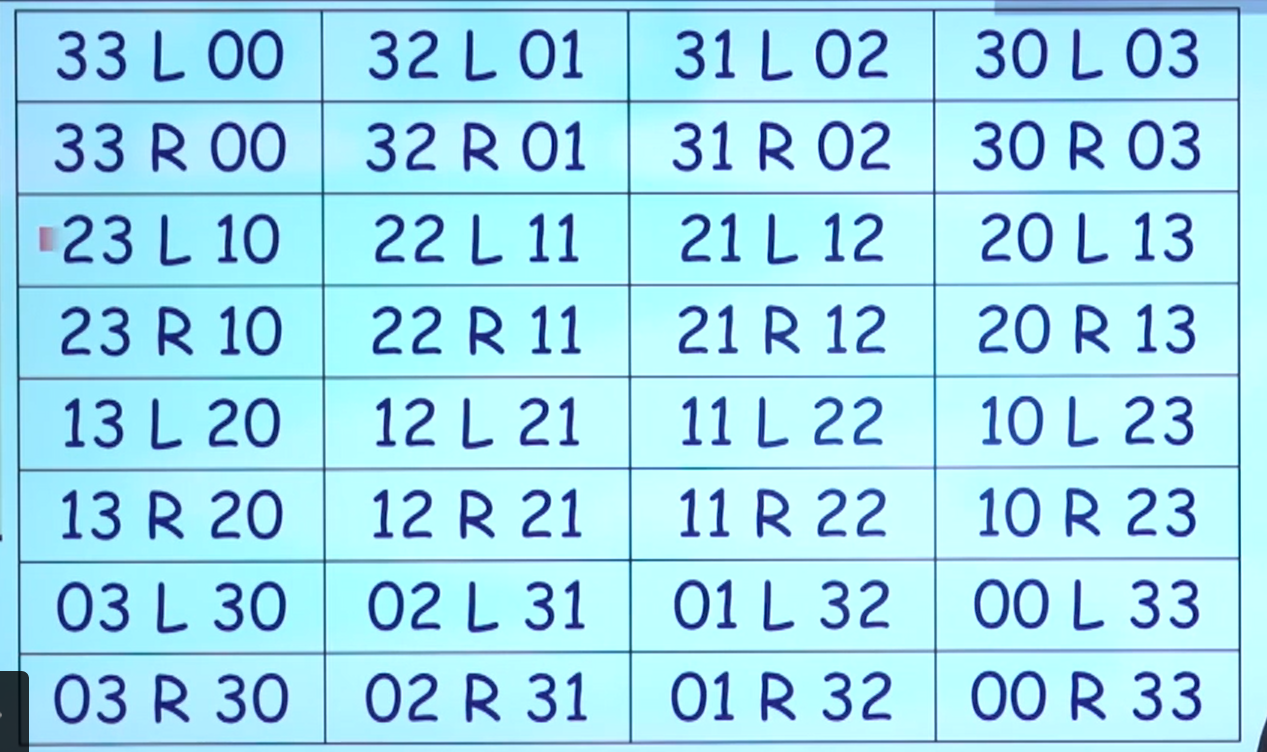
3、删除不合理状态
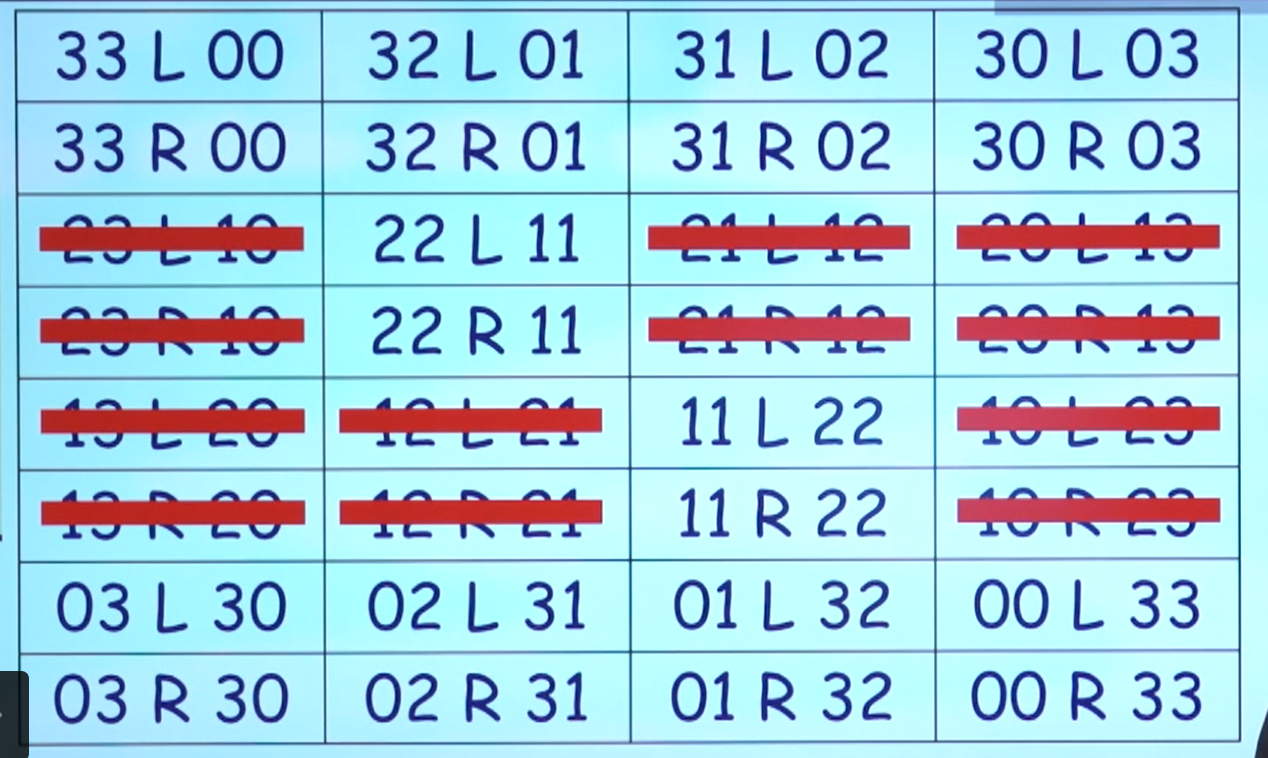
4、连边(模拟依次渡河变化)
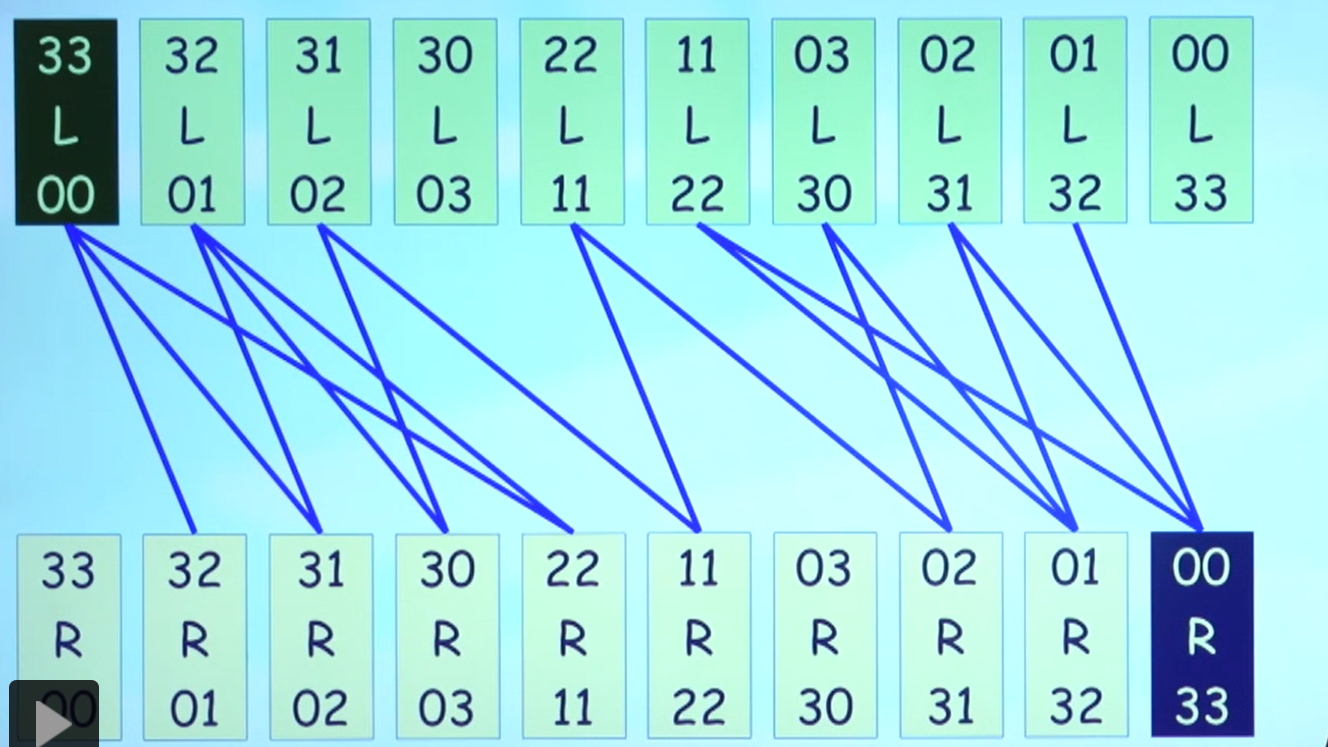
5、寻找路径
寻找(33 L 00)-->(00 R 33)的路径
其中一条路径 (33 L 00)-->(31 R 01)-->(32 L 01)-->(30 R 03)-->(31 L 02)-->(11 R 22)-->(22 L 01)-->(02 R 31)-->(03 L 30)-->(01 R 32)-->(02 L 31)-->(00 R 33) 1、两个吃人恶魔过河 2、一个吃人恶魔回来 3、两个吃人恶魔过河 4、一个吃人恶魔回来 5、两个传教士过河 6、一个传教士和一个吃人恶魔回来 7、两个传教士回来 8、一个吃人恶魔回去 9、两个吃人恶魔过河 10、一个吃人恶魔回去 11、两个吃人恶魔过河
四人过桥问题
问题描述
在一个漆黑的夜里,四位旅游者来到一座狭窄而没有护栏的桥边,如果不借助手电筒的话,大家是无论也不敢过去。不幸的是四个人中只有一只手电筒,而桥窄得只够两个人同时通过。如果各自单独过桥得话,四个人所需要的时间分别是1、2、5、10分钟,如果两个人同时过桥,所需要的时间是较慢的那个人单独行动时的时间。问:如何设计一个方案,让四个人尽快过桥。
解题思路
与前面两个相比,这次不仅要求方案,同时要求时间最短。
同样需要定义状态,四个人+手电筒的位置
1、定义状态
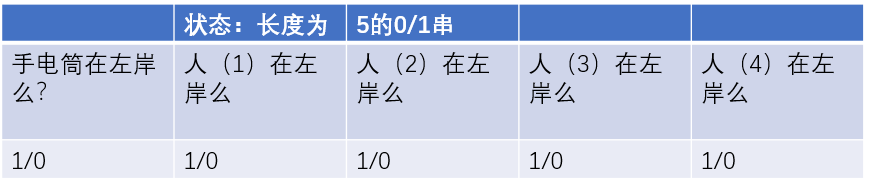
2、建图
分为每次通过一个人和每次两个人,都是带权无向边。
(下面只连接了与(01111)的边)

3、寻找最短路
寻找(L 1111)-->(R 0000)的最短路,即最短路算法中(01111)-->(10000)的最短路,以下是利用Dijstra算法的解决方法。
最终答案为(2 + 1 + 10 + 2 + 2) = 17.
1 #include<stdio.h> 2 #include<iostream> 3 #include<string> 4 #include<queue> 5 #include<algorithm> 6 using namespace std; 7 8 //定义图中结点 9 struct Node 10 { 11 int u, d; //该节点的编号与距离 12 bool operator < (const Node x) const 13 { 14 return d > x.d; 15 } 16 }; 17 18 //边结构体的定义 19 struct Edge 20 { 21 int to; 22 int w; 23 int next; 24 }; 25 26 const int INF = 0x3f3f3f3f; 27 const int V = 32 + 10; 28 const int E = 32 * 32 + 10; 29 int dis[V]; //源到各顶点的最短距离 30 int vis[V]; //记录是否被收录,用来代替集合S 31 int head[V]; //head[i]表示顶点i的第一条边的数组下标,"-1"表示顶点i没有边 32 Edge edge[E]; 33 34 inline void AddEdge(int a, int b, int w, int id) 35 { 36 edge[id].to = b; 37 edge[id].w = w; 38 edge[id].next = head[a]; 39 head[a] = id; 40 return; 41 } 42 43 //s为起点 44 void Dijsktra(int s) 45 { 46 priority_queue<Node>q; //取出集合T中的最小值 47 memset(vis, 0, sizeof(vis)); 48 memset(dis, INF, sizeof(dis)); 49 50 dis[s] = 0; 51 q.push(Node{ s, dis[s] }); 52 while (!q.empty()) 53 { 54 Node x = q.top(); q.pop(); 55 int u = x.u; 56 57 if (vis[u]) continue; 58 59 vis[u] = true; 60 for (int i = head[u]; i != -1; i = edge[i].next) //松弛与u直接相邻的顶点 61 { 62 int v = edge[i].to; 63 int w = edge[i].w; 64 if (!vis[v] && dis[u] + w < dis[v]) 65 { 66 dis[v] = dis[u] + w; 67 q.push(Node{ v,dis[v] }); 68 } 69 } 70 } 71 } 72 73 const int score[] = { 1,2,5,10 }; //每个人单独行动的时间 74 75 int main() 76 { 77 //建图 78 memset(head, -1, sizeof(head)); 79 int id = 0; 80 for (int i = 0; i < (1 << 4); i++) 81 { 82 int bits[4]; 83 for (int j = 0; j < 4; j++) bits[j] = (i >> j) & 1; 84 //一次走一个人 85 for (int j = 0; j < 4; j++) if (bits[j]) 86 { 87 int tmp = i - (1 << j) + 16; 88 int w = score[j]; 89 AddEdge(i, tmp, w, id++); 90 AddEdge(tmp, i, w, id++); 91 } 92 //一次走两个人 93 for(int j = 0;j < 3;j++) 94 for (int k = j + 1; k < 4; k++) if (bits[j] && bits[k]) 95 { 96 int tmp = i - (1 << j) - (1 << k) + 16; 97 int w = max(score[j],score[k]); 98 AddEdge(i, tmp, w, id++); 99 AddEdge(tmp, i, w, id++); 100 } 101 } 102 Dijsktra(15); 103 printf("%d\n", dis[16]); 104 105 return 0; 106 }
此类问题很多,但大多可用图论的思想做(虽然不一定是速度最快的),后续在补充吧,有问题直接留言!
参考链接:中国大学mooc 刘铎老师 离散数学


 浙公网安备 33010602011771号
浙公网安备 33010602011771号