牛顿迭代
牛顿迭代法(Newton's method)
又叫“牛顿-拉弗森方法”(Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法,方法是使用f(x)泰勒级数前几项来寻找f(y) = 0的根。
原理

对于非线性方程同样适用

总之,牛顿迭代公式:

应用
求某些方程的根
1 double a, b, c, d; 2 const double esp = 1e-6; 3 4 double f(double x){ 5 return a * x * x * x + b * x * x + c * x + d; 6 } 7 8 double fd(double x){ 9 return 3 * a * x *x + 2 * b * x + c; 10 } 11 12 //求解ax^3 + bx^2 + cx + d = 0的一个根 13 double newton(double x) 14 { 15 while (fabs(f(x)) > esp){x = x - f(x) / fd(x);} 16 return x; 17 }
如果想求出一个范围内的所有的跟,则可以在该范围内枚举初始值x,来逼近根的值。

1 #include<stdio.h> 2 #include<iostream> 3 #include<vector> 4 using namespace std; 5 6 double a, b, c,d; 7 const int INF = 0x3f3f3f3f; 8 const int maxn = 2; 9 const double esp = 1e-6; 10 double Abs(double x) 11 { 12 return x >= 0 ? x : -x; 13 } 14 double f(double x) 15 { 16 return a * x * x * x + b * x * x + c * x + d; 17 } 18 19 //需要f的导数在适当的区间内绝对值不大于于某个小于1的正数 20 double fd(double x) 21 { 22 return 3 * a * x *x + 2 * b * x + c; 23 } 24 25 //求解ax^3 + bx^2 + cx + d = 0的所有根 26 void newton() 27 { 28 vector<double>ans; 29 //在一个大区域中逐个点用牛顿法,可找出大多数3次方程所有根 30 for (int x0 = -maxn; x0 < maxn; x0++) 31 { 32 double x1 = x0; 33 int cnt = 0; //迭代次数 34 while (Abs(f(x1)) > esp) 35 { 36 if ((++cnt) > 10000) break; //迭代次数超过1000,认为方程无解 37 double x = x1; 38 x1 = x - f(x) / fd(x); 39 } 40 if (cnt > 10000) continue; 41 int flag = 0; 42 for(int i = 0;i < ans.size();i++) 43 if (Abs(ans[i] - x1) < 0.01) 44 { 45 flag = 1; 46 break; 47 } 48 if (!flag && x1 < INF && x1 > -INF) ans.push_back(x1); //x1==inf || -inf是在极值点,并不一定是方程的根 49 } 50 if (ans.size() == 0) printf("无解\n"); 51 else 52 { 53 for (int i = 0; i < ans.size(); i++) 54 printf("%lf ", ans[i]); 55 printf("\n"); 56 } 57 } 58 59 int main() 60 { 61 while (scanf("%lf%lf%lf%lf",&a,&b,&c,&d) == 4) 62 newton(); 63 64 return 0; 65 }
(这个代码测试起来有很多错误,有好的意见欢迎留言)
高精度开根号
对于一个已知的数 a,开根号本质上是求一个X,使得 X2=a,即X2 - a = 0的根。
由前面易知迭代公式Xn+1 = Xn - (Xn2 - a) / 2Xn = (Xn + a / Xn) / 2。
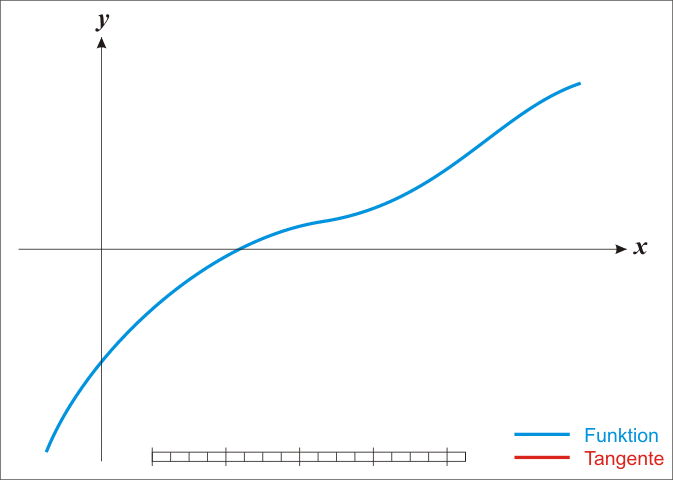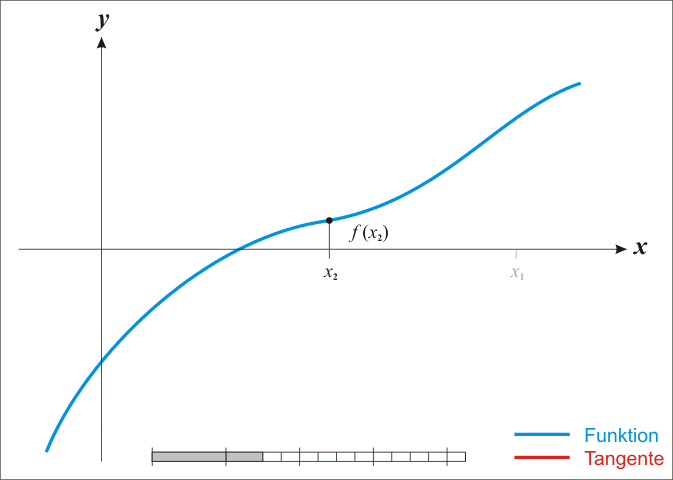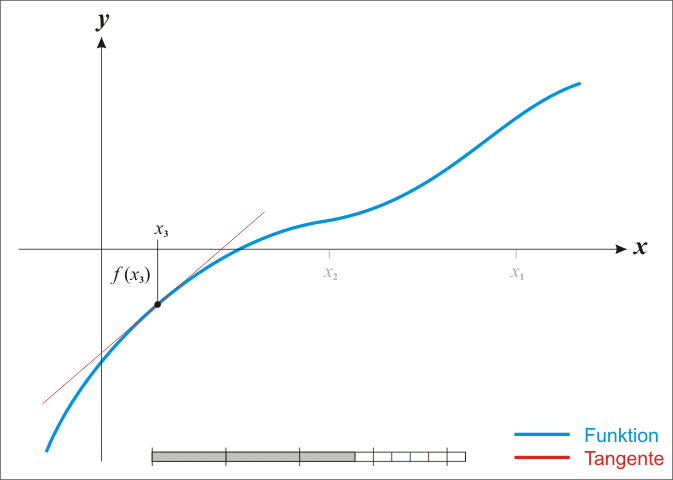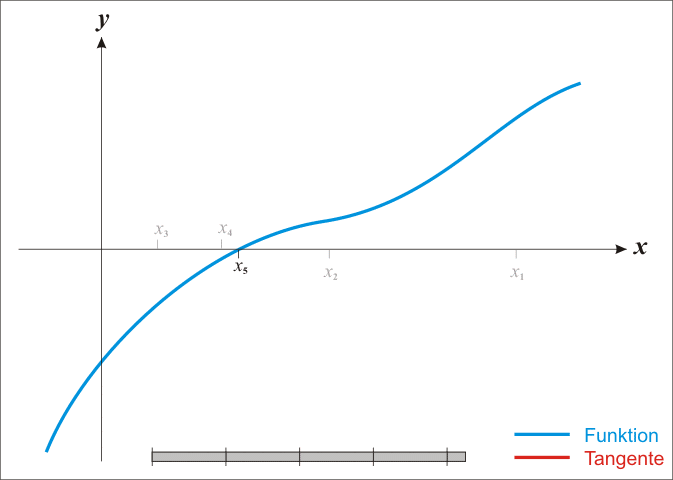
实际操作还需要套一个高精度除法。
缺点
并不能求解所有方程的根,而且得到的只是近似值,不是准确值。
收敛的充分条件:
若 f 二阶可导,那么在待求的零点 x 周围存在一个区域,只要起始点 x0 位于这个临近区域内,那么牛顿-拉弗森方法必定收敛。
驻点
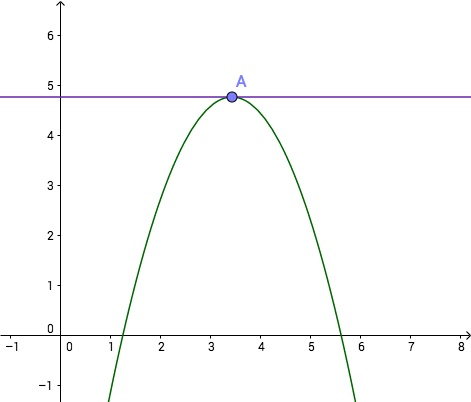
从代数上看,导数为0,无法迭代出下一个值。
越来越远的不收敛

循环震荡的不收敛

参考链接:
https://blog.csdn.net/wubaizhe/article/details/75574798
https://baike.baidu.com/item/牛顿迭代法/10887580?fr=aladdin#2
https://zh.wikipedia.org/wiki/牛顿法
https://www.zhihu.com/question/20690553
个性签名:时间会解决一切



 浙公网安备 33010602011771号
浙公网安备 33010602011771号