Kruskal与Prim
一、最小生成树
在无向图中，连通且不含圈的图称为树(Tree)。给定无向图G=(V,E),连接G中所有点，且边集是E的子集的树称为G的生成树(Spanning Tree),而权值最小的生成树称为最小生成树(Minning Spanning Tree,MST)。
二、Kruskal
步骤：
1、将所有的边按照从小到大的顺序排列
2、从小到大一次考量每条边(u,v)，如果u和v不在同一连通分量，那么把(u,v)加入连通分量
3、重复步骤2，直到图中所有节点都在同一连通分量中
图解：
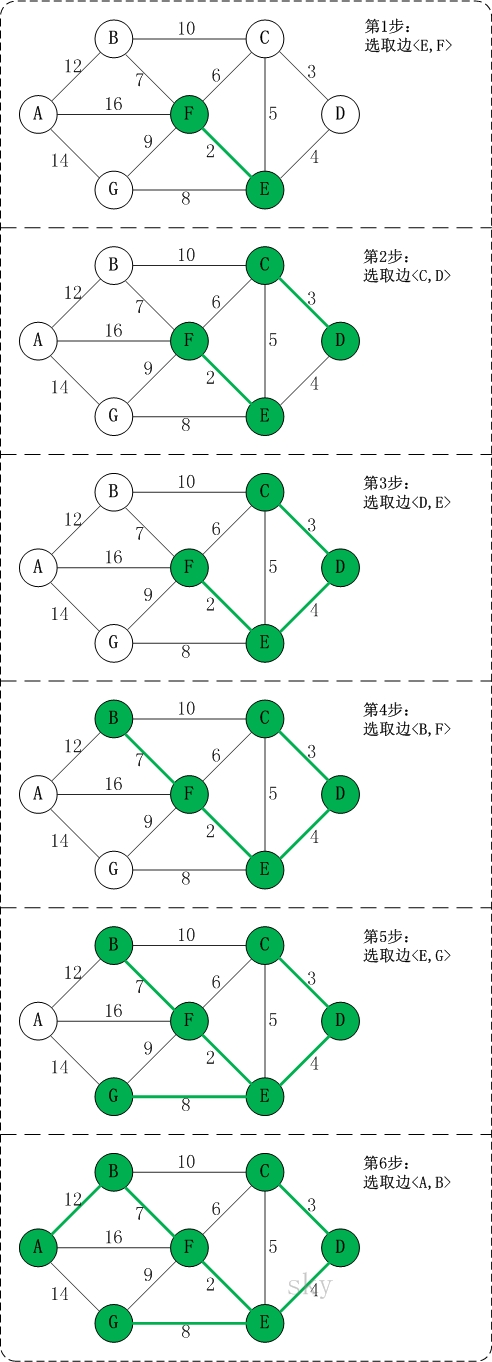
原理：
如果u和v在不同的连通分量中，那么加入(u,v)一定是最优的。为什么呢？
下面用反证法：如果这条边不在最小生成树中，它连接的两个连通分量最终还是要连起来的，通过其他的连法，那么另一种连法与这条边一定构成了环，而环中一定有一条权值大于这条边的边，用这条边将其替换掉，图仍旧保持连通，但总权值减小了。也就是说，如果不选取这条边，最后构成的生成树的总权值一定不会是最小的。
三、Prim
步骤：
1、初始化，Vnew = {x},其中x为集合V中的任意节点(起始点)，Enew = {}
2、在集合E中选取权值最小的边（u, v），其中u为集合Vnew中的元素，而v则是V中没有加入Vnew的顶点（如果存在有多条满足 前述条件即具有相同权值的边，则可任意选取其中之一）。将v加入集合Vnew中，将（u, v）加入集合Enew中；
3、重复操作2，直到Vnew = V
图解：
证明：
prim生成的树为T0, 最小生成树（MST）为Tmin
两棵树的边从小到大权重比较，设第一个属于 T0 但不属于 Tmin 的边为 ed1, 连接该边的两个顶点为 (vs, ve1)。同时存在第一个属 于 Tmin 但不属于 T0 的边为 ed2, 连接该边的两个顶点为 (vs, ve2)。
两个边的起点相同。由Prim算法性质可知，w(ed2) >= w(ed1)。
此时，在 Tmin 中删除 ed2 ，添加 ed1，边的数量和顶点数量均不变，且不存在环，因此得到新的生成树Tnew,且cost(Tmin)>=cost (Tnew)。又因为 Tmin 是MST 所以 cost(Tmin)=cost(Tnew)。
