Dijkstra算法——单源最短路算法
一、介绍
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他各个节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
适用于有向图和无向图,但不能有边权为负的情况。
二、基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未确定最短路径的顶点(以及该顶点到起点s的距离)。
需要一个数组dis记录起点到各顶点的最短距离,初始化,dis[s] = 0,dis[v] = w,v与s右边时,其他dis[u] = INF。
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径(这是因为新加入的顶点只会影响与之直接相连的点)。然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 ... 重复该操作,直到遍历完所有顶点。
三、正确性
不严谨的理解,S是以收录的顶点,最短距离已经确定,U是未确定的顶点;我们只需证明每次U中的最小值C(dis[C]),就是其最短距离。反证法:假如C到原点的最短距离不是dis[C],即存在中间点V,使得先到V再到C更近,如果V在集合S中,由于集合S中的所有顶点已经起作用,再经过S距离不会小于dis[C];如果V在集合U中,由于dia[C]已经是U中最小的了,途径其他点也不会小于dis[C]。所以我们可以每次都收录U中的最小的。
四、Dijkstra的图解
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
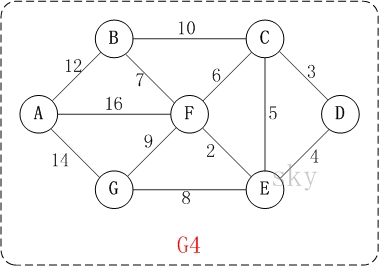
以G4这个图为例,进行算法演示(以第四个顶点D为起点)
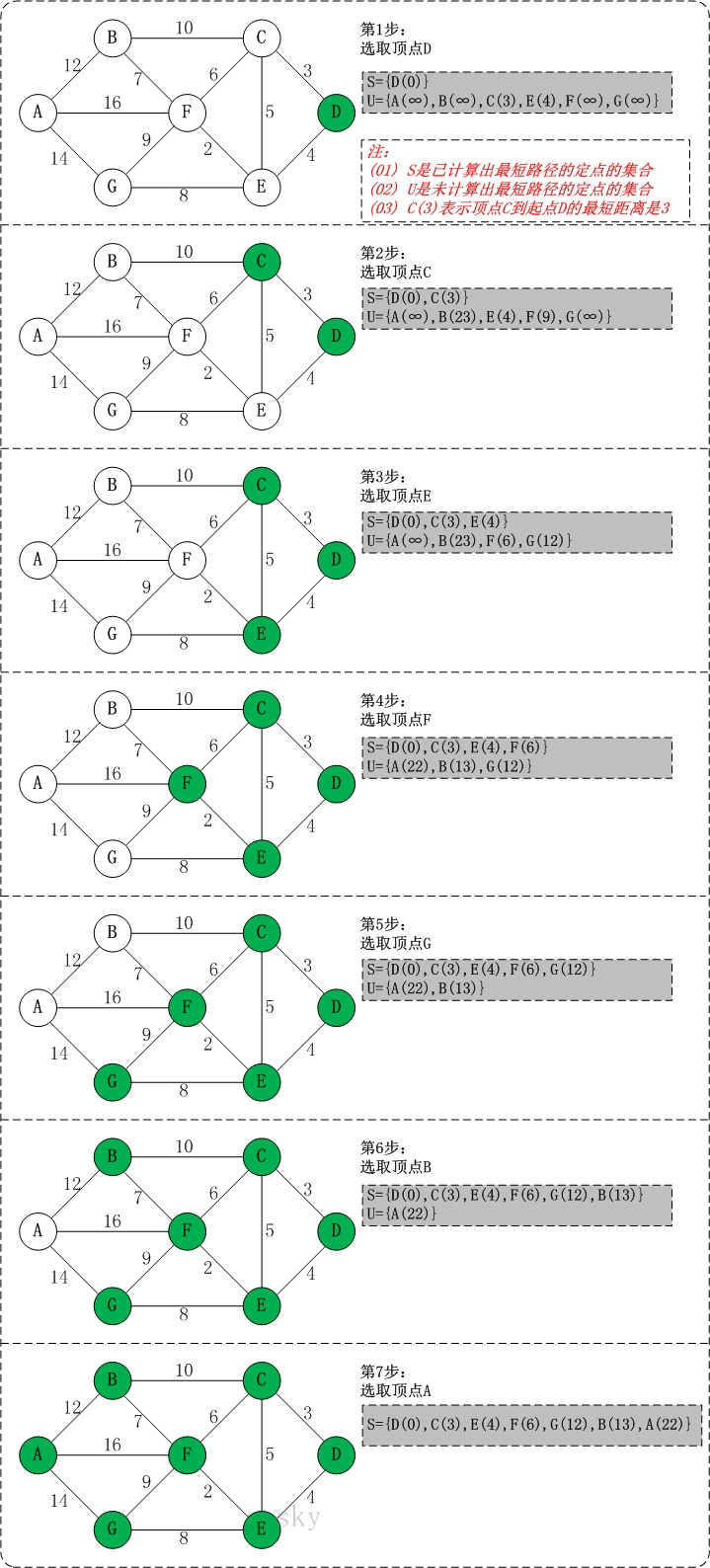
五、一个有趣的辩论:Dijkstra算法的本质是贪心还是动态规划
一般意义上的贪心算法在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
Dijkstra算法显然是从整体最优考虑,求出的最短路径,一定是整体最优解,这是和一般意义上的贪心算法相悖的地方。而且Dijkstra算法符合动态规划的这一特性:待求解的问题分解为若干个子问题,前一子问题的解,为后一子问题的求解提供了有用的信息。在我看来,Dijkstra算法更接近动态规划。

