木板切割问题——贪心

一、问题引入

农夫约翰为了修理栅栏，要将一块很长的木块切成N块。准备切成的长度分别是L1、L2、、、，L_N,未切割前的木板长度切好为切割后木板长度的总和。每次切断木板时的开销是这块木板的长度。（1 ≤ N ≤ 20000，0 ≤ L_i ≤ 50000）

二、解题思路

由于N的值非常大，不可能枚举所有情况再求解，必须用一种比较高效的算法。木板的切割循序不确定，看似自由度很高，是先选择切出较短的，还是切较长的。如果我们把一种完全切割后的情况列举出来，会发现可以用贪心算法

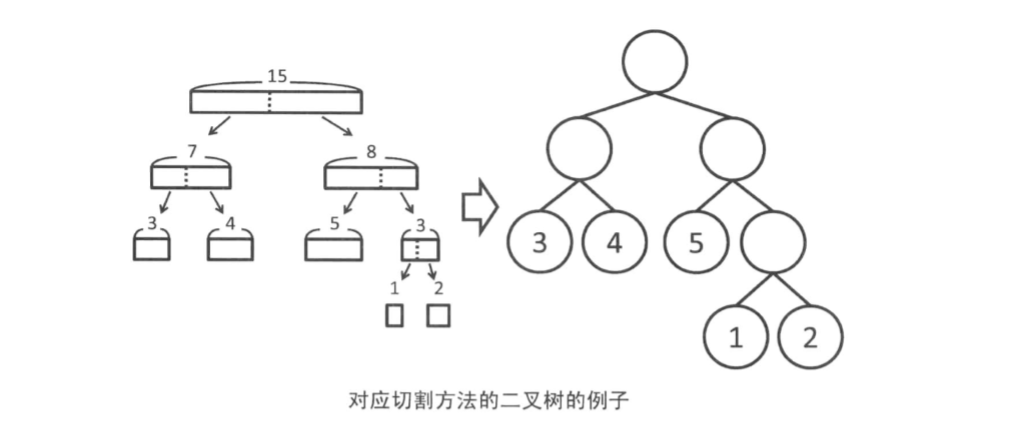
惊奇的发现，这种切法的切割费用之和 == 所有非叶子节点权值和 == 叶子节点的权值 * 深度（根节点深度为0）

即 33 = 15 + 7 + 8 + 3 = 3*2 + 4*2 + 5*2 + 1*3 + 2*3

问题转化为，已知所有的叶子节点和根节点，求叶子节点的权值 * 深度和的最小值。

显然，使权值大的深度小，权值小的深度大。于是，此时的最佳切割方法应该具有如下性质：

　　　　最短版和次短板应该是兄弟节点

这一性质在切割过程中始终成立，反过来，我们可以根据这种性质建立起对应的二叉树。即每次合并最小的，合并后的值加到总费用中。（注意建立的树不唯一，但每种的结果一样，所以选其中一种就行）

由于是每次取最小和次小合并，维护一个优先队列就行

三、代码实现

#include<stdio.h>
#include<iostream>
#include<queue>
using namespace std;

typedef long long LL;
const int maxn = 20000 + 10;
int n, L[maxn];

void slove()
{
    LL ans = 0;

    //声明一个小值在前的优先队列
    priority_queue<int, vector<int>, greater<int>>que;
    for (int i = 0; i < n; i++)
        que.push(L[i]);

    //循环到只剩一块模板为止
    while (que.size() > 1)
    {
        //取出最短的木板和次短的木板
        int len1, len2;
        len1 = que.top(); que.pop();
        len2 = que.top(); que.pop();

        ans += (len1 + len2);
        que.push(len1 + len2);
    }
    printf("%lld\n", ans);
}

int main()
{
    while (scanf("%d",&n) == 1)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", &L[i]);
        slove();
    }
    return 0;
}

四、总结

这个题运用了很多哈夫曼树的思想，下一篇文章再讨论吧。