箭袋图和流图
在本节中,您将学习如何使用Matplotlib构建箭袋图(quiver)和流图(stream plots)。
Quiver Plots
Quiver是一种2D图,它将矢量线显示为箭头。箭袋图在电气工程中用于可视化电势,在机械工程中用于显示应力梯度。
只有一个箭头的Quiver
首先,我们将构建一个包含一个箭头的简单quiver图,以演示Matplotlib的ax.quiver()方法是如何工作的。ax.quiver()方法有四个位置参数:
ax.quiver(x_pos, y_pos, x_direct, y_direct)
其中x_pos和y_pos是箭头的起始位置,x_direct和y_direct是箭头的方向。
我们的第一个图在起点x_pos = 0, y_pos = 0处包含一个箭袋箭头。箭袋箭头的方向是向上指向右边的x_direct = 1, y_direct = 1。
下面的代码部分构建了一个包含一个箭矢的箭袋图。
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
%matplotlib inline
fig, ax = plt.subplots()
x_pos = 0
y_pos = 0
x_direct = 1
y_direct = 1
ax.quiver(x_pos, y_pos, x_direct, y_direct)
ax.set_title('Quiver plot with one arrow')
plt.show()

箭袋图包含一支箭。箭头从点0,0开始,止于点1,1。
有两个箭头的Quiver
现在让我们通过传递两个起始点和两个箭头方向向箭袋图添加第二个箭头。
我们将原始箭头的起始位置保持在原点0,0处,并向上和向右(在1,1方向上)。我们将定义第二个箭头,起始位置为-0.5,0.5,它指向竖直向下(在0,-1方向)。
添加ax.quiver()方法的另一个关键字参数是scale=5。包含scale=5可以缩放箭头的长度,这样箭头看起来更长,在quiver图上显示得更好。
要查看两个箭头的开始和结束,我们将使用ax.axis()方法设置轴限制在-1.5和1.5之间,并传入一个形式为[xmin, xmax, ymin, ymax]的轴限制列表。我们可以看到两个箭头。一个箭头指向右上方,另一个箭头指向正下方。
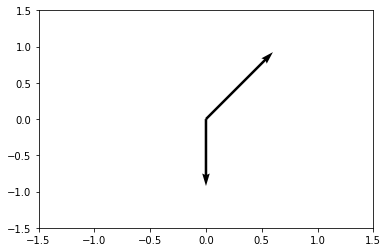
我们看到一个有两个箭头的图。两支箭都从原点开始。一个箭头指向右上方,另一个箭头指向正下方。
使用网格画Quiver
一个有两个箭头的箭袋图是一个很好的开始,但是一个一个地添加箭袋图箭头是乏味和重复的。为了创建一个完整的箭的2D曲面,我们将利用NumPy的meshgrid()函数。
首先,我们需要构建一组数组,用于表示图上每个箭袋的x和y起始位置。颤箭的起始位置数组将被称为X和Y。我们可以使用x、y箭头起始位置来定义每个箭袋箭头方向的x和y分量。我们将箭袋箭头方向数组称为u和v。
对于这个图,我们将根据箭袋箭头起点使用方程来定义箭袋箭头方向:
接下来的代码块使用NumPy中的np.meshgrid()构建X和Y位置数组
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
%matplotlib inline
x = np.arange(0,2.2,0.2)
y = np.arange(0,2.2,0.2)
X, Y = np.meshgrid(x, y)
u = np.cos(X) * Y
v = np.sin(y) * Y
接下来,我们可以使用Matplotlib中的ax.quiver()构建箭袋图,调用ax.quiver()接受4个位置参数:
ax.quiver(x_pos, y_pos, x_direct, y_direct)
在这个箭袋图中,x_pos和y_pos是包含箭头起始位置的2D数组,x_direct, y_direct是包含箭头方向的2D数组。
命令ax.xaxis.set_ticks([])和ax.yaxis.set_ticks([])删除轴上的标记。·ax.set_aspect ('equal')将绘图的纵横比设置为1:1。
fig, ax = plt.subplots(figsize=(7,7))
ax.quiver(X,Y,u,v)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
ax.axis([-0.2, 2.3, -0.2, 2.3])
ax.set_aspect('equal')
plt.show()

现在让我们构建另一个箭袋图,其中\(\hat{i}\) 和 \({\hat{j}}\) 是箭头的分量,\(\hat{F}\)
x = np.arange(-1,1,0.1)
y = np.arange(-1,1,0.1)
X,Y = np.meshgrid(x,y)
u = X/5
v = -Y/5
fig, ax = plt.subplots(figsize=(9,9))
ax.quiver(X,Y,u,v)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
ax.set_aspect('equal')
plt.show()

含有一个梯度的Quiver
接下来让我们构建一个显示梯度函数的箭袋图。梯度函数有这样的形式:
我们可以使用NumPy的np .gradient()函数将梯度函数应用到每个箭头的x, y起始位置。
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
%matplotlib inline
x = np.arange(-2,2.2,0.2)
y = np.arange(-2,2.2,0.2)
X, Y = np.meshgrid(x, y)
z = X*np.exp(-X2 -Y2)
dx, dy = np.gradient(z)
fig, ax = plt.subplots(figsize=(9,9))
ax.quiver(X,Y,dx,dy)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
ax.set_aspect('equal')
plt.show()

有4个旋涡的Quiver
现在让我们建立一个包含四个漩涡的箭袋图。函数\(\hat{F}\)描述了包含四个漩涡的2D场,如下图所示。
下面的代码部分构建了一个带有四个漩涡的颤振图:
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
%matplotlib inline
x = np.arange(0,2 * np.pi+2 * np.pi/20,2 * np.pi/20)
y = np.arange(0,2 * np.pi+2 * np.pi/20,2 * np.pi/20)
X,Y = np.meshgrid(x,y)
u = np.sin(X) * np.cos(Y)
v = -np.cos(X) * np.sin(Y)
fig, ax = plt.subplots(figsize=(9,9))
ax.quiver(X,Y,u,v)
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
ax.axis([0,2 * np.pi,0,2 * np.pi])
ax.set_aspect('equal')
plt.show()

画带有颜色的Quiver
最后,让我们为我们的箭袋图添加一些颜色。ax.quiver()方法有一个可选的第五个位置参数,用于指定箭袋箭头的颜色。quiver箭头颜色参数需要与位置和方向数组具有相同的维度:
ax.quiver(x_pos, y_pos, x_direct, y_direct, color)
使用Matplotlib子图,我们可以构建一个包含三个箭袋图的图。每个箭袋图都将是彩色的。
下面的代码部分将构建一个包含三个子图的图形。每个子图都是一个彩色箭袋图。
import numpy as np
import matplotlib.pyplot as plt
fig, (ax1,ax2,ax3) = plt.subplots(1,3)
# first subplot
x = np.arange(0,2.2,0.2)
y = np.arange(0,2.2,0.2)
X, Y = np.meshgrid(x, y)
u = np.cos(X) * Y
v = np.sin(y) * Y
n = -2
color = np.sqrt(((v-n)/2)*2 + ((u-n)/2)*2)
ax1.quiver(X,Y,u,v,color, alpha=0.8)
ax1.xaxis.set_ticks([])
ax1.yaxis.set_ticks([])
ax1.axis([-0.2, 2.3, -0.2, 2.3])
ax1.set_aspect('equal')
ax1.set_title('meshgrid function')
# second subplot
x = np.arange(-2,2.2,0.2)
y = np.arange(-2,2.2,0.2)
X, Y = np.meshgrid(x, y)
z = X*np.exp(-X**2 -Y**2)
dx, dy = np.gradient(z)
n = -2
color = np.sqrt(((dx-n)/2)*2 + ((dy-n)/2)*2)
ax2.quiver(X,Y,dx,dy,color)
ax2.xaxis.set_ticks([])
ax2.yaxis.set_ticks([])
ax2.set_aspect('equal')
ax2.set_title('gradient')
# third subplot
x = np.arange(0,2*np.pi+2*np.pi/20,2*np.pi/20)
y = np.arange(0,2*np.pi+2*np.pi/20,2*np.pi/20)
X,Y = np.meshgrid(x,y)
u = np.sin(X) * np.cos(Y)
v = -np.cos(X) * np.sin(Y)
n = -1
color = np.sqrt(((dx-n)/2)*2 + ((dy-n)/2)*2)
ax3.quiver(X,Y,u,v,color)
ax3.xaxis.set_ticks([])
ax3.yaxis.set_ticks([])
ax3.axis([0,2*np.pi,0,2*np.pi])
ax3.set_aspect('equal')
ax3.set_title('four vortices')
# save and show the figure
plt.tight_layout()
fig.savefig('./quiver/3_quiver_plots.png', dpi=300, bbox_inches='tight')
plt.show()

3D的Quiver
%reset -f
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
fig = plt.figure()
ax = fig.gca(projection='3d')
x, y, z = np.meshgrid(np.arange(-0.8, 1, 0.2),
np.arange(-0.8, 1, 0.2),
np.arange(-0.8, 1, 0.8))
u = np.sin(np.pi * x) * np.cos(np.pi * y) * np.cos(np.pi * z)
v = -np.cos(np.pi * x) * np.sin(np.pi * y) * np.cos(np.pi * z)
w = (np.sqrt(2.0 / 3.0) * np.cos(np.pi * x) * np.cos(np.pi * y) *
np.sin(np.pi * z))
ax.quiver(x, y, z, u, v, w, length=0.1, color = 'black')
plt.show()

流图
流图是一种用于显示流体流动和2D场梯度的2D图。
在Matplotlib中构建流图的基本方法是:
ax.streamplot(x_grid,y_grid,x_vec,y_vec, density=spacing)
其中x_grid和y_grid是数组的x和y点。数组x_vec和y_vec表示网格上每个点的流速度。关键字参数density=spacing指定流线画在一起的紧密程度。
一个简单的流图
让我们从包含10 x 10网格上的流线的流图开始。图上所有的流线都是平行的,并且指向右边。
下面的代码部分构建了一个流图,其中包含指向右侧的水平平行线。
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
%matplotlib inline
x = np.arange(0,10)
y = np.arange(0,10)
X, Y = np.meshgrid(x,y)
u = np.ones((10,10)) # x-component to the right
v = np.zeros((10,10)) # y-component zero
fig, ax = plt.subplots()
ax.streamplot(X,Y,u,v, density = 0.5)
ax.set_title('Stream Plot of Parallel Lines')
plt.show()

图中包含了平行的流线,都指向右边。
一个场的流图
我们可以建立一个流图,显示基于定义的2D矢量场(field)的场线。
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
%matplotlib inline
x = np.arange(0,2.2,0.1)
y = np.arange(0,2.2,0.1)
X, Y = np.meshgrid(x, y)
u = np.cos(X)Y
v = np.sin(y)Y
fig, ax = plt.subplots()
ax.streamplot(X,Y,u,v, density = 1)
ax.axis([0.5,2.1,0,2])
ax.xaxis.set_ticks([])
ax.yaxis.set_ticks([])
ax.set_title('Stream Plot of Field Lines')
plt.show()

两个点电荷的流图
最后,我们将建立一个流图来演示由两个点电荷引起的电场。二维曲面上任意一点上的电场取决于相对于两个点电荷的位置和距离。
import numpy as np
import matplotlib.pyplot as plt
# if using a Jupyter notebook, include:
x = np.arange(-4,4,0.2)
y = np.arange(-4,4,0.2)
X,Y = np.meshgrid(x,y)
Ex = (X + 1)/((X+1)**2 + Y**2) - (X - 1)/((X-1)**2 + Y**2)
Ey = Y/((X+1)**2 + Y**2) - Y/((X-1)**2 + Y**2)
fig, ax = plt.subplots(figsize=(6,6))
ax.streamplot(X,Y,Ex,Ey)
ax.set_aspect('equal')
ax.plot(-1,0,'-or')
ax.plot(1,0,'-ob')
ax.set_title('Stream Plot of Two Point Charges')
plt.savefig("./quiver/plot_streamplot.png")
plt.show()

参考链接:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号