计算机视觉的基本原理——光流法

转载自 [多目标跟踪学习笔记]光流法, 运动重构与目标跟踪，有少量补充
光流法是进行目标跟踪的传统方法，参照视频 进行学习

1. 运动场(Motion Field)和光流(Optical Flow)

光流, 顾名思义就是光的流动. 对于图像来说, 什么是光的流动呢? 想象一下摄像头是运动的(目标是运动的也一样), 目标的运动变化其实就是"像素点"的"移动", 因此称为光流, 如下图所示:

如上图所示, 假如摄像头是移动的, 那么这棵树的亮度模式就会发生变化, 那么发生变化的这个趋势实际上就代表了目标的运动.

问题1: 那么, 我们认为的所谓像素点亮度模式的变化和目标真实的运动之间有什么关系呢?

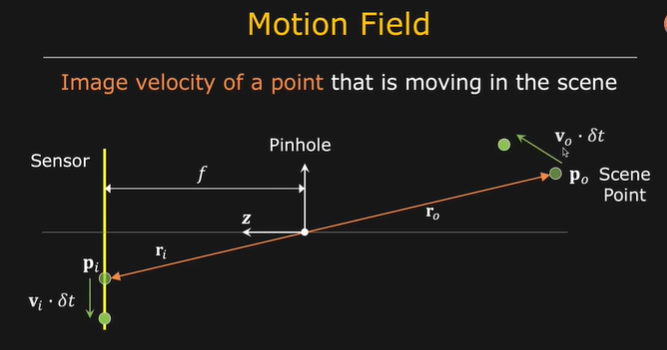
问题2: 运动场和光流是等价的吗?

答案是否定的. 请看以下几种情况:

1. 有运动场 无光流 或 有光流, 无运动场
   下图的左边, 假设球体是旋转的, 但是光源不动. 是有运动场, 无光流的情形.右边反之, 球体是不动的, 但光源是运动的.

2. 光流和运动场并不相等
   这个例子更直接. 例如理发店门口的彩灯, 我们知道真实的物理运动是水平向右的, 然而, 如果关注像素亮度的变化, 则光流的方向是向下的, 二者正好垂直.

2. 光流约束方程

我们如何更好地通过光流来估计运动呢?

首先我们要做一些假设, 这样问题才可以进行下去. 我们考虑以下连续的两帧图片:

这张图片中鹰是运动的目标，如果我们关注其中一个像素\((x, y)\)，假定下一帧的位置在\((x+\delta x, y+\delta y)\)，我们可以得到该像素点的速度(也就是亮度运动模式, 理论上的光流方向):

\[(u, v)=(\delta x / \delta t, \delta y / \delta t) \]

假设1 两帧间的对应像素亮度不变

我们认为 \(\delta t\)足够小，以至于不会使我们关注的像素点在两帧之间产生亮度变化，假设亮度用\(I(.)\)来表示，有：

\[I(x,y,) = I(x+ \delta x, y + \delta y, t + \delta t) \]

我们对等号右边进行多元函数的Taylor展开, 并忽略二次项及以上的高阶项, 有:

\[I(x+\delta x, y+\delta y, t+\delta t)=I(x, y, t)+\frac{\partial I}{\partial x} \delta x+\frac{\partial I}{\partial y} \delta y+\frac{\partial I}{\partial t} \delta t \]

联立上两式, 有:

\[\frac{\partial I}{\partial x} \delta x+\frac{\partial I}{\partial y} \delta y+\frac{\partial I}{\partial t} \delta t=0 \]

令\(\delta t \rightarrow 0\)，两边同时除以\(\delta t\)，有:

\[\frac{\partial I}{\partial x} \frac{\delta x}{\delta t}+\frac{\partial I}{\partial y} \frac{\delta y}{\delta t}+\frac{\partial I}{\partial t}=0 \]

式中的\(\frac{\partial x}{\partial t}\), \(\frac{\partial x}{\partial t}\) 分别为光流真值(速度)\(u,v\)，故将上式写成：

\[I_x u+I_y v+I_t=0 \]

以上就是光流约束方程.

求解上式中\(I_x, I_y, I_t\)的方式与图像处理中求梯度的方式类似，固定一个变量求其余变量得到差，例如\(I_x\)按如下计算：

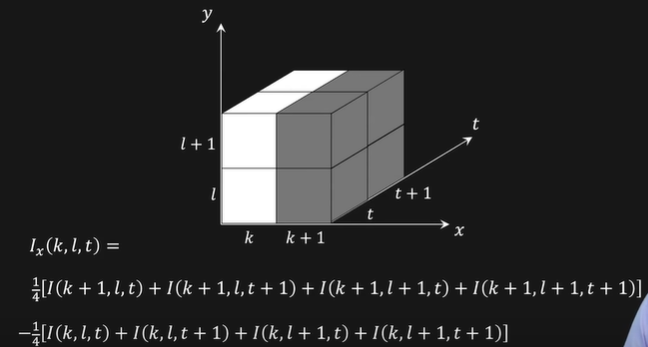
好，现在我们知道了\(I_x, I_y, I_t\)。式子\(I_x u+I_y v+I_t=0\)规定了一条直线，\(u,v\)落在这条直线上，但是我们无法获取准确的值

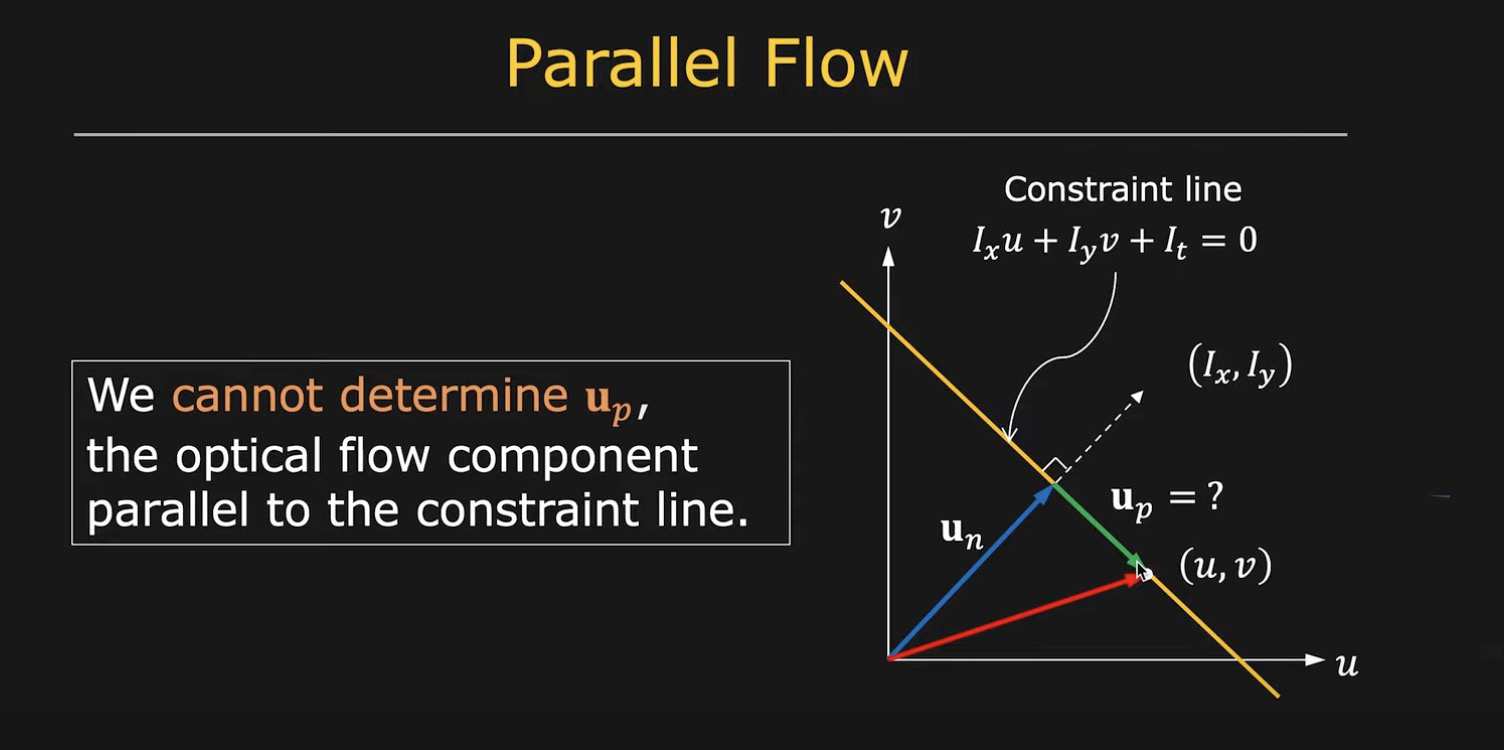
具体地, 如上图, 假设光流真值为 \(\boldsymbol{u}=(u, v)\)，我们将其分解为垂直直线方向与平行直线方向\(\boldsymbol{u}=\boldsymbol{u}_n+\boldsymbol{u}_p\)
根据几何知识, 很快求得:

\[\boldsymbol{u}_{\boldsymbol{n}}=\frac{\left|I_t\right|}{\sqrt{I_x^2+I_y^2}}\left(I_x, I_y\right) \]

然而，\(\boldsymbol{u_p}\)我们不知道，因此需要更多的约束条件.

3. Lucas Kanade算法

接上文, 我们需要更多的约束条件. Lucas Kanade算法所做的假设是:

假设2 假定对于每个像素, 运动场与光流和其邻域中的像素均相同

假设某像素的某领域为\(W\)，大小为\(n \times n\)的矩形，则对\(W\)中的每个像素\((k, l) \in W\)，光流都相同，因此有：

\[I_x(k, l) u+I_y(k, l) v+I_t(k, l)=0,(k, l) \in W \]

上面是\(n^2\)个方程，我们写成矩阵的形式：

\[\left[\begin{array}{cc} I_x(1,1) & I_y(1,1) \\ \ldots & \ldots \\ I_x(n, n) & I_y(n, n) \end{array}\right]\left[\begin{array}{l} u \\ v \end{array}\right]=\left[\begin{array}{c} -I_t(1,1) \\ \ldots \\ -I_t(n, n) \end{array}\right] \]

记为：

\[\boldsymbol{A} \boldsymbol{u}=\boldsymbol{B}, A \in \mathbb{R}^{n^2 \times 2}, u=[u, v]^T, B \in \mathbb{R}^{n^2 \times 1} \]

\(n^2\)这个数有点大，为了方便计算，我们将方程写为：

\[\left(A^T A\right) u=A^T B \]

其中\(\boldsymbol{A}^{\boldsymbol{T}} \boldsymbol{A} \in \mathbb{R}^{2 \times 2}\)，假设$\boldsymbol{A}^{\boldsymbol{T}} \boldsymbol{A} $可逆，有：

\[u=\left(A^T A\right)^{-1} A^T B \]

可以看到，光流估计值本质上就是\(n^2\)个约束方程\(A u= B\)的最小二乘解，因此就求解出光流了. 然而, LK算法以上的求解方式也有其局限性, 必须要求:

1. \(A^T A\)可逆
2. \(A^T A\)必须是well-conditioned. 所谓的well-conditioned 就是指其两个特征值$ \lambda_1, \lambda_2$满足：

• \(\lambda_1>\epsilon\) and \(\lambda_2>\epsilon\)，即两者都是正数，且不能太小
• \(\lambda_1 \geq \lambda_2\) 但不要 \(\lambda_1>>\lambda_2\)

weil-conditioned的意义是, 如果特征值都太小, 则求解出的u uu也很小, 结果不可靠.
如果两个特征值相差很大, 则并不能确保具体的运动方向.

4. 粗糙到精细的光流估计(光流金字塔, Coarse to fine estimation)

LK算法有一个先验假设，即\(\delta t\)足够小, 也就是小运动假设. 但如果运动范围很大的时候, 怎么做呢?
我们可以降低图片的分辨率, 例如通过池化的方式, 这样原来的大运动就会变成小运动. 如下图所示.

转化成小运动之后, 我们就可以利用之前的算法在低分辨率图像上求解光流了.
假定我们有四种分辨率, 从低到高是1, 2, 3, 4. 在1分辨率上, 我们利用小运动的估计来计算光流\(OP\), 假设结果为\({u, v)}^0\).

这样, 我们在2分辨率上利用1分辨率上计算出的光流, 产生一个新的图像(类似于插帧). 这个图像会更接近原始分辨率的运动, 但不精确. 这一步叫做"Wrap".

因此, 同样地我们对插帧后的2分辨率再计算光流, 得到插帧到最终图像的光流变化\(\Delta(u, v)^1\). 因此此时我们可以得到更精确的光流估计\((u, v)^1=(u, v)^0+\Delta(u, v)^1\)，这一步叫做"Plus".

再对3分辨率上应用此光流插帧, 一直这样下去. 如图所示:

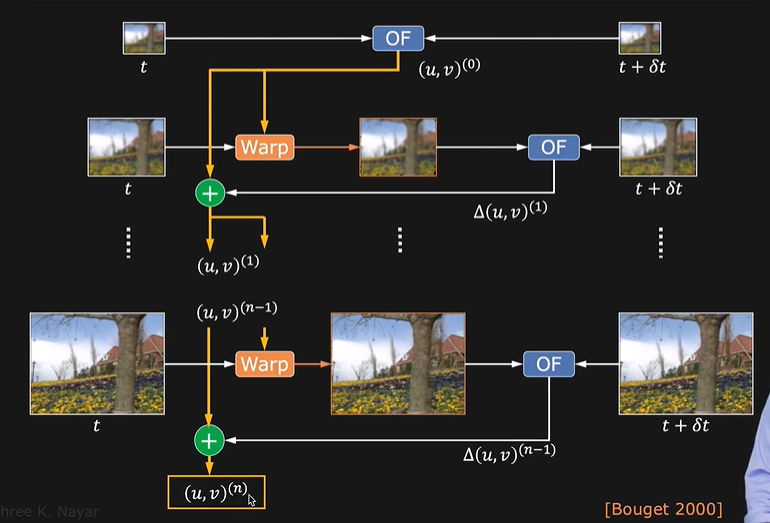
因此, 我们就从粗糙分辨率的小运动, 一步一步估计到了精细分辨率的大运动, 总之是一个Warp+Plus的迭代过程.

5. 替代方法：模板匹配(Alternative approach: Template Matching)

约束方程只有一个，而方程的未知量有两个，这种情况下无法求得u和v的确切值。此时需要引入另外的约束条件，从不同的角度引入约束条件，导致了不同光流场计算方法。按照理论基础与数学方法的区别把它们分成四种：基于梯度（微分）的方法、基于匹配的方法、基于能量（频率）的方法、基于相位的方法和神经动力学方法

上面的金字塔方法(基于梯度) 工作的很好，但是为了完整性，这里再介绍另外一种方法，一种暴力的计算光流的方法

从\(t\)时刻的图像中取一小块，在\(t+\delta t\)时刻的图像中找到相似的，两个窗口的连线就是光流.

这显然具有非常大的计算量，对图像中的每个像素都要执行上述操作，并且在匹配的时候较远距离的像素块也可能相同，这显然是无意义的。因此，通常的做法是在领域搜索，并提前终止.