圆环上随机取3个点组成一个锐角三角形的概率

问题rt，有很多解决方法。
先说结论，锐角三角形的概率是 \(\frac{1}{4}\)，钝角三角形的概率是 \(\frac{3}{4}\) ，直角三角形的概率是 \(0\).

1. 微积分

如下图所示：

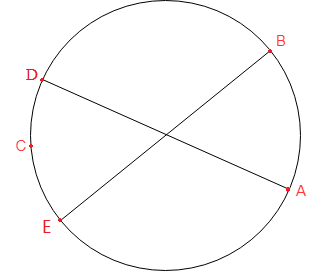
取单位圆上任意两点点A和B，若ABC三点要够成锐角三角形，则点C必须在DE之间。
设弧AB对应的圆心角为\(\theta\)，易知\(\theta\)的概率密度为\(\frac{1}{\pi}\)，C点在AB对应的DE段间的概率是\(\frac{\theta}{2\pi}\)，因此三个点组成一个锐角三角形的概率为

\[\int_0^\pi \frac{1}{\pi}\cdot\frac{\theta}{2\pi}\mathrm{d}\theta = \frac{\theta ^ 2}{4\pi ^ 2}\bigg|_0^\pi = \frac{1}{4} \]

2. 几何概型

易知，问题等价于将 \(2\pi\) 分成 \(\alpha, \beta, \gamma\)，且都小于\(\pi\)。即

\[\begin{eqnarray} \alpha + \beta + \gamma & = & 2\pi \\ \alpha & < & \pi \\ \beta & < & \pi \\ \gamma & < & \pi \\ \end{eqnarray} \]

而样本空间是 \(0 < \alpha < 2\pi , 0 < \beta < 2\pi, 0 < \gamma < 2\pi, \alpha+\beta+\gamma = 2\pi\)，

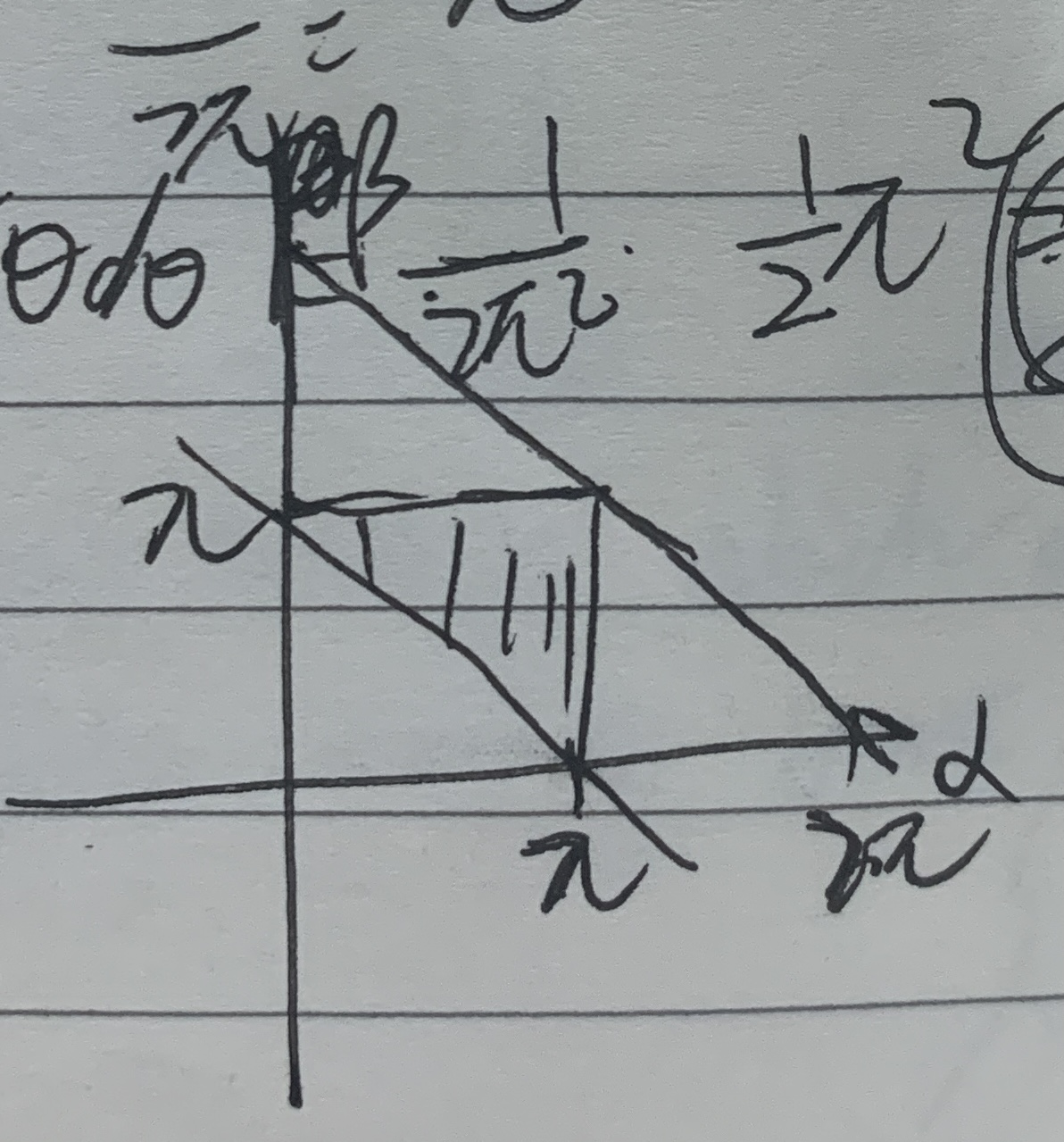
计算一下面积比可得\(\frac{1}{4}\)

参考链接

1. 圆上任选三点组成三角形，这个三角形是锐角、钝角和直角三角形的概率分别是多少？ - inversioner的回答 - 知乎
2. 圆环上随机取3个点组成一个锐角三角形的概率