笔记：自动求导【动手学深度学习v2】
沐神 视频链接
自动求导
自动求导是指计算一个函数在指定值上的导数
注意是求导数的具体值，而不是求求导公式
计算图
计算图
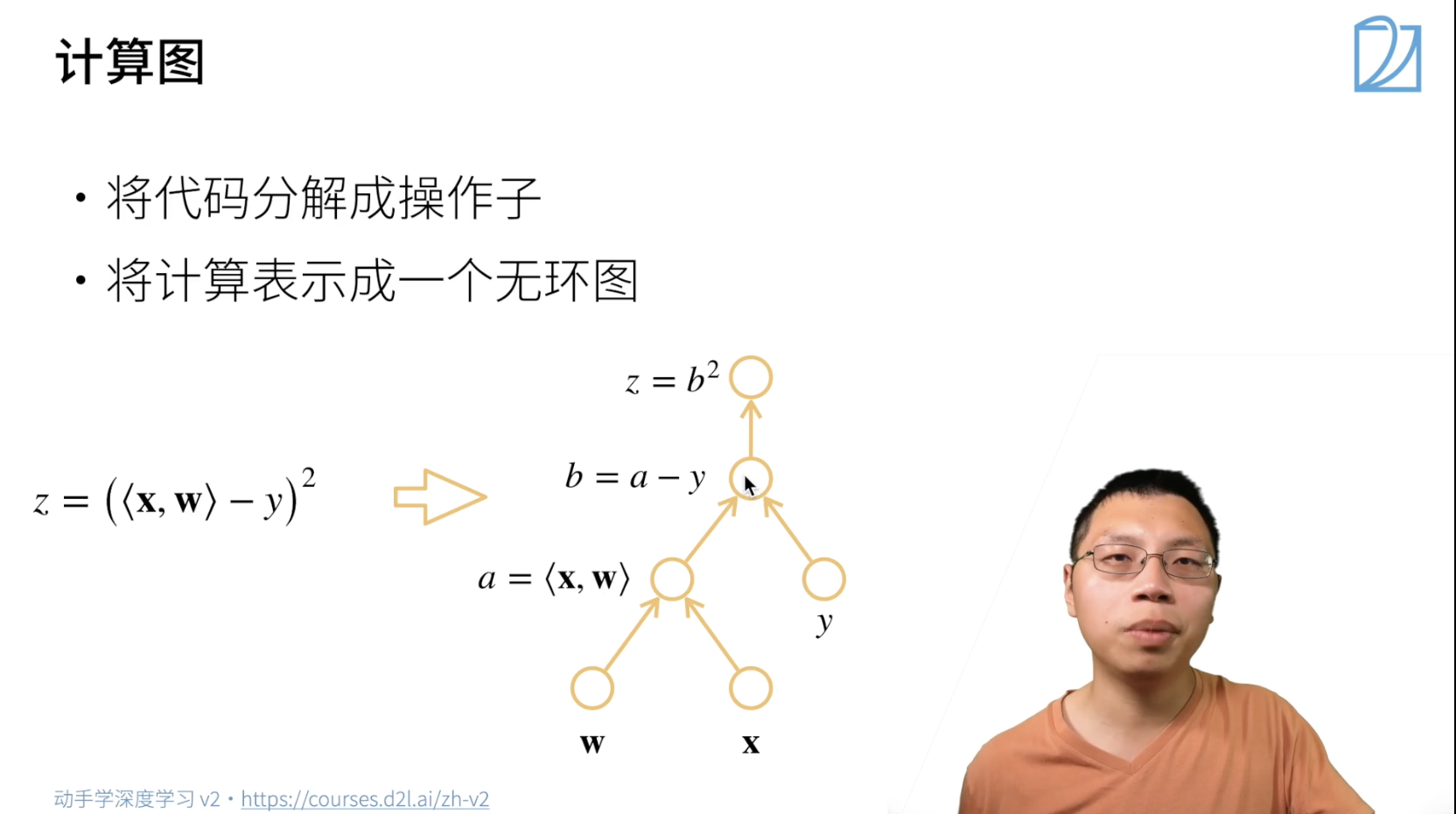
就是一个DAG
分为隐式构造和显式构造：
显式是指用公式定义的计算图（静态），隐式是指用python控制流定义的计算图（动态）
自动求导的方式
有两种计算导数的方法，因为链式求导只是将导数乘起来，顺序可以自定义，下面将的都是采用反向计算导数
反向计算导数的过程
首先正向计算值，并把中间结果存在对应节点
然后反向传递计算导数的值，可能需要用到节点的值，例如下面的 \(\frac{\partial z}{\partial b}\) 和 \(\frac{\partial z}{\partial \mathbf{w}}\)
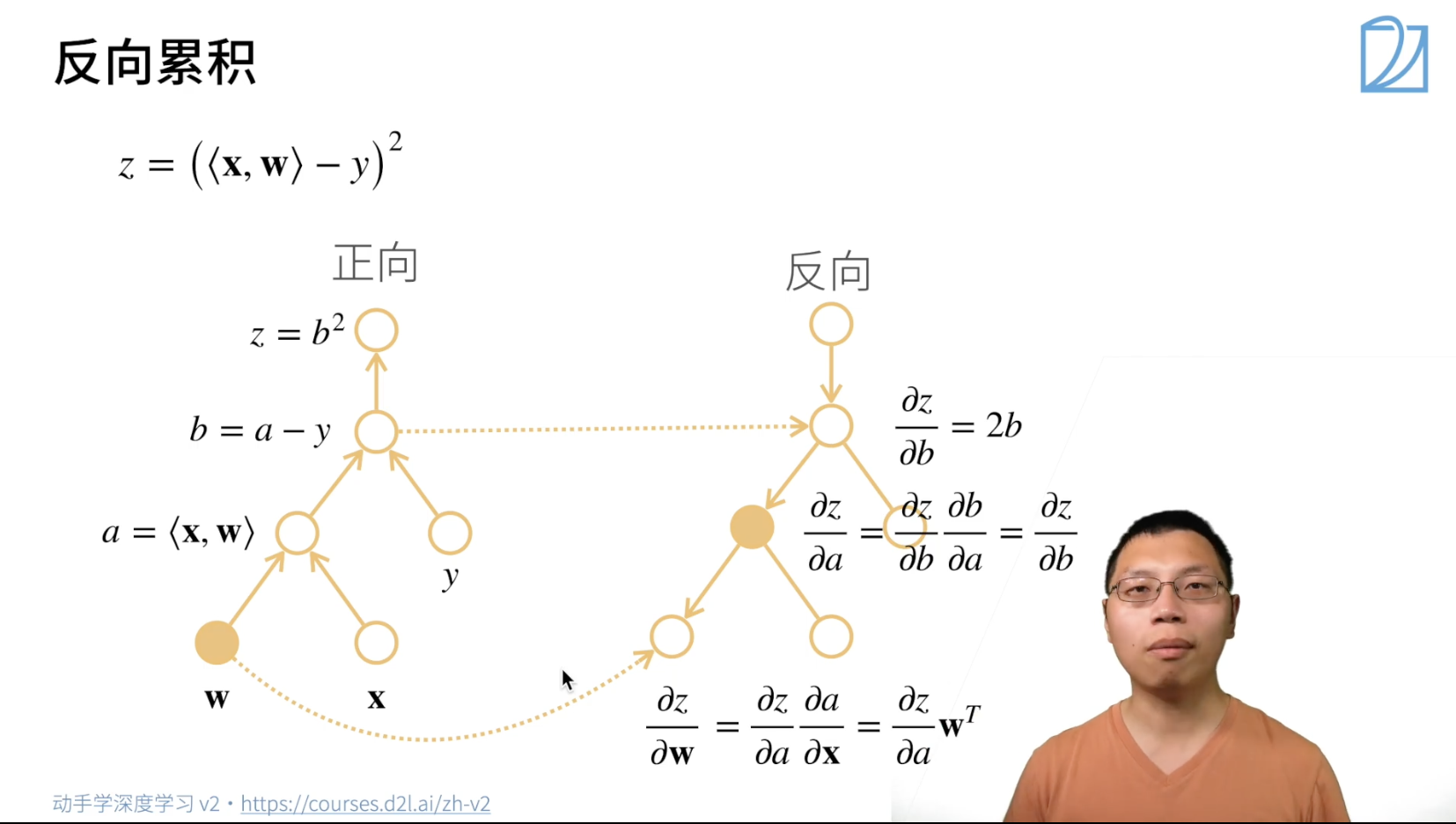
其中，反向传递时可以不计算没用到的分支
总结
正向(forward)和反向(backword)的时间复杂度差不多，但是正向需要记录所有的中间值，空间复杂度会高一些，
存起来，这也是深度神经网络特别耗GPU内存的祸源
与正向求导相比，反向求导可以一次性计算完梯度，而正向求导每次求梯度都需要将后面的图扫一遍
复杂度
Hands on try
反向传播才会计算梯度
点击查看代码
import torch
x = torch.arange(4.0)
print(x)
x.requires_grad_(True)
x.grad # 默认值为None，存梯度的地方
y = 2 * torch.dot(x, x) # y = 2x^2, y.grad = 4x
y.backward() # 通过调用反向传播来自动计算y对x每个元素的梯度
print(x.grad)
print(x.grad == 4 * x)
Out:
tensor([0., 1., 2., 3.])
tensor([ 0., 4., 8., 12.])
tensor([True, True, True, True])
如果将 y 定义为 x.sum，梯度会变成多少呢
点击查看代码
x.grad.zero_() # 清空梯度
y = x.sum() # y = x1 + x2 + x3 + x4
y.backward()
print(x.grad) # 所以对每个分量的梯度都是1
Out:
tensor([1., 1., 1., 1.])
如果将 x.grad.zero_() 注释掉呢？会发现梯度累加了
点击查看代码
Out:
tensor([ 1., 5., 9., 13.])
如果是对非标量求导呢？
在深度学习中，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和
深度学习中很少到非标量求和，对非标量求导需要加 gradient 参数
如果出现这种情况，通常会对非标量求一个 sum
点击查看代码
# 对非标量直接调用backward()会报错
# 需要给backward()传入一个gradient参数，参数的形状和x一样，可以是标量
# 或者用sum()将非标量转换为标量
x.grad.zero_()
y = x * x
y.sum().backward() # 等价于 y.backward(torch.ones_like(y))
print(x.grad) # 所以对每个分量的梯度都是2
Out:
tensor([0., 2., 4., 6.])
使用 detach 将某些操作移到计算图外，被 detach 的向量会变成一个标量，不再有梯度了
这在固定部分参数的时候很有用
点击查看代码
x.grad.zero_()
y = x * x
u = y.detach() # u是一个标量，不会被求导
z = u * x
z.sum().backward()
print(x.grad == u)
x.grad.zero_()
y.sum().backward() # y还是x的导数，但u不是了
print(x.grad == 2 * x)
Out:
tensor([True, True, True, True])
即使计算图是通过python控制流构建的，我们仍然可以计算变量的梯度
这是一个动态图，图的结构与输入有关
因为在正向执行图的时候，Pytorch会将计算图存下来，因此反向的时候知道怎么算
点击查看代码
def f(a):
b = a * 2
while b.norm() < 1:
b = b * 2
if b.sum() > 1:
c = b / b.sum()
else:
c = b
return c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
print(a.grad)
在运行反向传播函数之后，立即再次运行它，看看会发生什么？
会出错
因为pytorch默认backward()后回将节点的值free(清空)，前面我们知道计算梯度需要用到节点的值
点击查看代码
d.backward()
d.backward()
Out:
RuntimeError: Trying to backward through the graph a second time (or directly access saved variables after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved variables after calling backward.
