树状数组总结篇

树状数组的作用很简单，单点修改+区间求和。

单点修改的话有两种，改变多少（add, sub）和改成多少（set），不过后者可以转化为前者，模板一般也是按照前者写的。

原理的话，这里不细节讲，网上很多；

求和：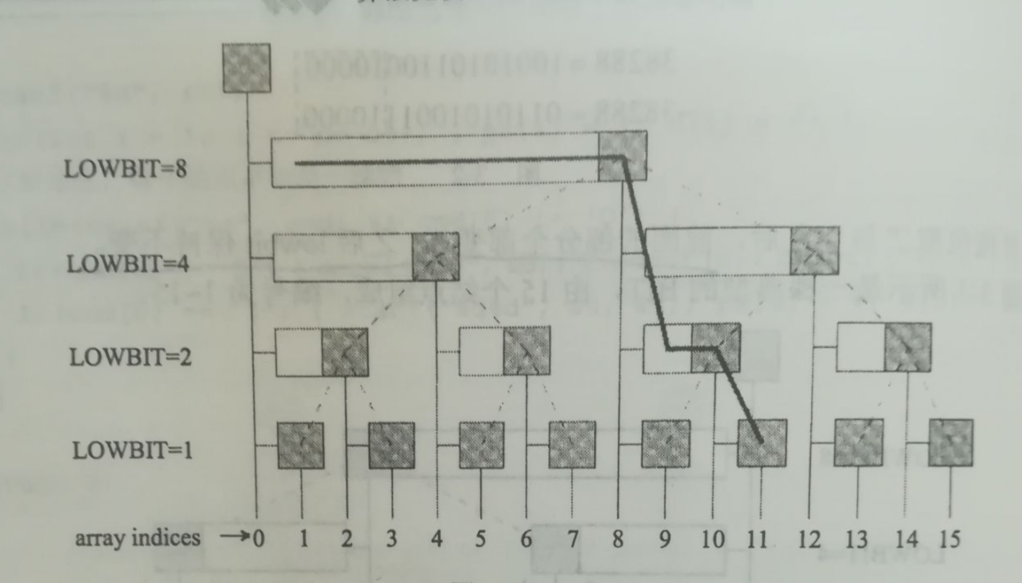

11的二进制：1011，分成长度分别为1, 2, 8的段累加，每减一次lowbit(x)，消掉一个1.

单点修改：

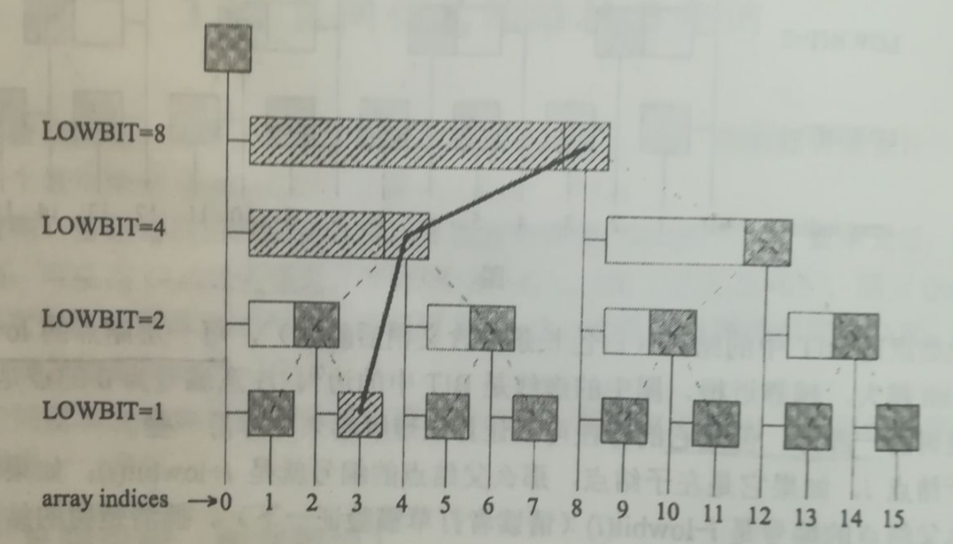
修改第3个时，3=b` 11, 每次加lowbit(x)，可以消除x的最低位1，当消完所有的1，x所影响的节点也就修改完了。

实现起来也算简单，add：不断加lowbit(x)直到n，sum：不断减lowbit(x)直到0，init: 清空a,c数组，逐个add.

应用：就两大类，对于ai

1. 将第ai个加1：例如求逆序对(leetcode493)、计算右侧小于当前元素的个数(leetcode315)

2. 将第i个加ai：例如求区间和(leetcode307)

模板（leetcode版）

    struct BIT{
        // static const int maxn = 2e4+10;
        // int c[maxn], n;
        vector<int>c;
        int n;
        void init(int _n)
        {
            n = _n;
            c.resize(n+1, 0);
            // memset(c, 0, sizeof(c));  
        }
        int lowbit(int x) { return x & -x; }
        int sum(int x)
        {
            int ret = 0;
            while(x)
            {
                ret += c[x];
                x -= lowbit(x);
            }
            return ret;
        }
        void add(int x, int val)
        {
            while(x <= n)
            {
                c[x] += val;
                x += lowbit(x);        
            }
        }
    }bit;