打印二叉树的右视图

解法一：BFS+记录dep深度

如果某节点dep小于下一个节点，说明该节点是本层的最右节点。如果该节点弹出后队列为空，同样该节点也是最右节点。

    vector<int> rightSideView(TreeNode* root) {
        if(root == NULL)  return vector<int>{};
        vector<int>res;
        queue<pair<TreeNode*, int>>q;
        q.push(make_pair(root, 0));
        while(!q.empty())
        {
            TreeNode* p = q.front().first;
            int dep = q.front().second;
            q.pop();
            if(q.empty() || dep < q.front().second)  // 队列为空说明该节点一定是最右节点（否则不可能为空）
                res.push_back(p->val);
            
            if(p->left != NULL)
                q.push(make_pair(p->left, dep+1));
            if(p->right != NULL)
                q.push(make_pair(p->right, dep+1));
        }
        return res;
    }

 

解法二：dfs

如果按照先根节点，再右子树，再左子树，那么观察到一个结论：每当访问到一个新深度，该节点就是最右节点。

 

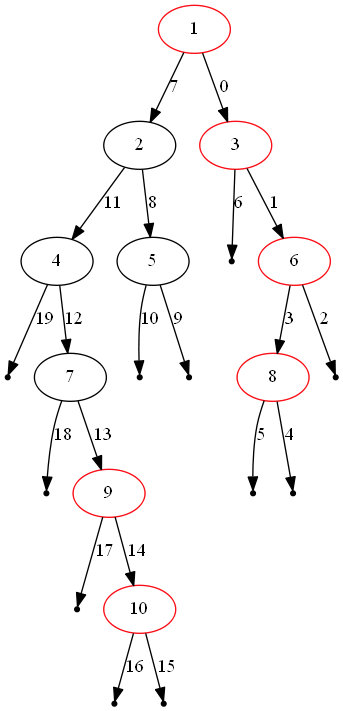
    vector<int>res;   // 存储最右节点
    int max_dep = -1;  // 当前最大深度
    vector<int> rightSideView(TreeNode* root) {
        PostOrder(root, 0);
        return res;
    }
    void PostOrder(TreeNode* root, int dep)
    {
        if(root == NULL)  return;
        if(dep > max_dep)
        {
            res.push_back(root->val);
            max_dep = dep;
        }
        PostOrder(root->right, dep+1);
        PostOrder(root->left, dep+1);
    }

显然，右视图改变一下遍历顺序就可以了。

 

参考链接：

1. https://leetcode-cn.com/problems/binary-tree-right-side-view/solution/you-xian-you-zi-shu-de-shen-du-bian-li-qing-xi-gao/

2. https://leetcode-cn.com/problems/binary-tree-right-side-view/solution/er-cha-shu-de-you-shi-tu-by-leetcode/