遗传算法(二)——求单变量函数的最值
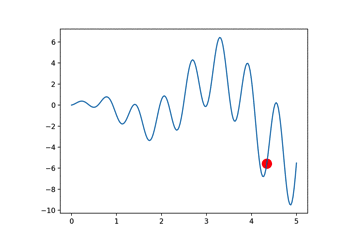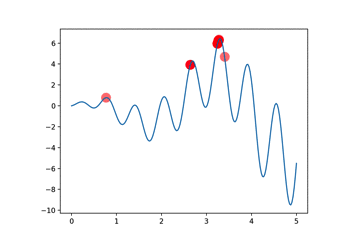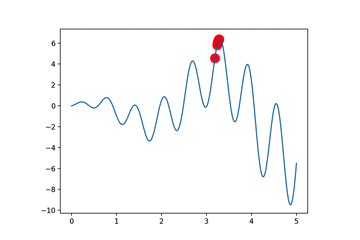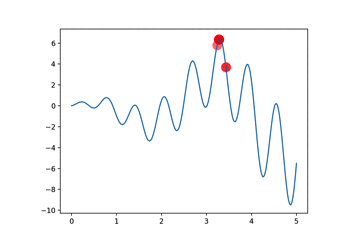
要想使用遗传算法,首要任务是定义DNA编码。
传统的 GA 中, DNA 我们能用一串二进制来表示, 比如:
DNA1 = [1, 1, 0, 1, 0, 0, 1]
DNA2 = [1, 0, 1, 1, 0, 1, 1]
这里,我们仍然使用二进制编码,但是如何与我们的问题对应起来呢?
我们知道二进制很容易转十进制,再区间压缩以下,这样一个DNA和一个解一一映射。
def translateDNA(pop): return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1]
例如,1 0 1 0 1 0 0 1 0 0 => (4+32+128+256)/(1024-1)*(5-0)=3.3
完整代码:
""" Visualize Genetic Algorithm to find a maximum point in a function. Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/ """ import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 10 # DNA length POP_SIZE = 100 # population size CROSS_RATE = 0.8 # mating probability (DNA crossover) MUTATION_RATE = 0.003 # mutation probability N_GENERATIONS = 100 X_BOUND = [0, 5] # x upper and lower bounds def F(x): return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function #def F(x): return -x*(x-2) # find non-zero fitness for selection def get_fitness(pred): return pred + 1e-3 - np.min(pred) # convert binary DNA to decimal and normalize it to a range(0, 5) # 1 0 1 0 1 0 0 1 0 0 => (4+32+128+256)/(1024-1)*(5-0)=3.3 def translateDNA(pop): return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * (X_BOUND[1]-X_BOUND[0]) def select(pop, fitness): # nature selection wrt pop's fitness idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True, p=fitness/fitness.sum()) return pop[idx] def crossover(parent, pop): # mating process (genes crossover) if np.random.rand() < CROSS_RATE: i_ = np.random.randint(0, POP_SIZE, size=1) # select another individual from pop cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool) # choose crossover points parent[cross_points] = pop[i_, cross_points] # mating and produce one child return parent def mutate(child): for point in range(DNA_SIZE): if np.random.rand() < MUTATION_RATE: child[point] = 1 if child[point] == 0 else 0 return child # pop是100*10的随机01矩阵 pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE)) # initialize the pop DNA # 绘制原始函数图像 plt.ion() # something about plotting x = np.linspace(*X_BOUND, 200) plt.plot(x, F(x)) for _ in range(N_GENERATIONS): F_values = F(translateDNA(pop)) # compute function value by extracting DNA # something about plotting if 'sca' in globals(): sca.remove() sca = plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5); plt.pause(0.05) # GA part (evolution) fitness = get_fitness(F_values) print("Generation: ", _) print("Most fitted DNA: ", pop[np.argmax(fitness), :]) print("Most fitted Value: ", translateDNA(pop[np.argmax(fitness), :])) pop = select(pop, fitness) pop_copy = pop.copy() for parent in pop: child = crossover(parent, pop_copy) child = mutate(child) parent[:] = child # parent is replaced by its child plt.ioff(); plt.show()
参考链接:莫凡PYTHON-遗传算法
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号