JZOJ3492数数&&GDOI2018超级异或绵羊——位&&类欧几里得
JZOJ3492 数数(count)
我们知道,一个等差数列可以用三个数A,B,N表示成如下形式:
B+A,B+2A,B+3A⋯B+NA
ztxz16想知道对于一个给定的等差数列,把其中每一项用二进制表示后,一共有多少位是1
A<=1e4,B<=1e16,N<=1e12
分析:
有个很经典的类欧套路,k从0开始
二进制下,第k位是否为1,等于(原数>>k)-2*(原数>>(k+1)),
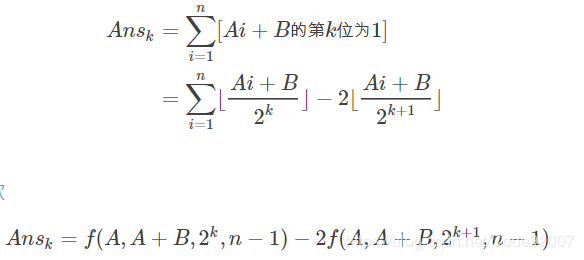
可以把i从1到n变成i从0到n-1,也就是提一个A出来,再做,于是就是类欧板子题。

#include<bits/stdc++.h> using namespace std; typedef long long ll; ll f(ll a, ll b, ll c, ll n) { if(!a) return (b/c)*(n+1); if(a >= c || b >= c) return (f(a%c, b%c, c, n) + n*(n+1)/2*(a/c) + (n+1)*(b/c)); ll m = (a*n+b) / c; return (n*m - f(c, c-b-1, a, m-1)); } ll a, b, n; int main() { int T; scanf("%d", &T); while(T--) { scanf("%lld%lld%lld", &a, &b, &n); ll limit = b + a*n, ans = 0; for(int mi = 1; mi <= limit; mi*=2) ans += f(a, a+b, mi, n-1) - f(a, a+b, mi*2, n-1)*2; printf("%lld\n", ans); } return 0; }
【GDOI2018模拟8.8】超级绵羊异或
求(a) xor (a + b) xor (a + b * 2) xor … xor (a + b * (n - 1))。
对于100%的数据,t<=1e4,a, n<=1e9, b<=1e9;
分析:
还是用上面那一个套路,
写成求和形式,考虑最后第k位的奇偶,即像上题一样,判断每一位的出现次数,对每一位使用类欧。

#include<bits/stdc++.h> using namespace std; typedef long long ll; ll f(ll a, ll b, ll c, ll n) { if(!a) return (b/c)*(n+1); if(a >= c || b >= c) return (f(a%c, b%c, c, n) + n*(n+1)/2*(a/c) + (n+1)*(b/c)); ll m = (a*n+b) / c; return (n*m - f(c, c-b-1, a, m-1)); } ll a, b, n; int main() { int T; scanf("%d", &T); while(T--) { scanf("%lld%lld%lld", &n, &a, &b); ll limit = a + b*(n-1), ans = 0; for(int mi = 1; mi <= limit; mi*=2) { ll tmp = f(b, a, mi, n-1) - f(b, a, mi*2, n-1)*2; ans += (tmp&1)*mi; } printf("%lld\n", ans); } return 0; }
BZOJ3817
给定正整数N,R。求
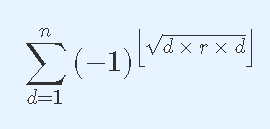
分析:
继续用上面的套路,考虑幂的奇偶会对答案造成不同贡献,本质上是幂的第1位是否为1,即求 $Ans_0$.
因为底数是-1,对布尔式的贡献线性变换一下,搞成1-2*Ans0。
由于sqrt(r)是实数,不能完全当整数处理,


$\begin{align}
f(a,b,c,n) &= \left \lfloor \frac{bx+c}{a} \right \rfloor\frac{n(n+1)}{2} + \sum_{i=1}^{\left \lfloor \frac{bx+d}{a}n \right \rfloor}n-\frac{a}{bx+d}i \\
&= \left \lfloor \frac{bx+c}{a} \right \rfloor\frac{n(n+1)}{2} + \left \lfloor \frac{bx+d}{a} n \right \rfloor n - \sum_{i=1}^{\left \lfloor \frac{bx+d}{a}n \right \rfloor} \left \lfloor \frac{a}{bx+d}i \right \rfloor
\end{align}$
将后面和式里的东西分母有理化得
$f(a,b,c,n) = S-\sum_{i=1}^{\left \lfloor \frac{bx+d}{a}n \right \rfloor}\left \lfloor \frac{abx-ad}{b^2x^2-d^2}i \right \rfloor = S - f(b^2r-d^2, ab, -ad, \left \lfloor \frac{bx+d}{a}n \right \rfloor)$
于是递归求,类似于辗转相除,递归层数不超过 $log_2n$.

#include<bits/stdc++.h> using namespace std; typedef long long ll; ll n, r; ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; } double x; ll f(ll a, ll b, ll c, ll n) { if(!n) return 0; ll t = gcd(a, gcd(b, c)); a/= t, b/=t, c/=t; ll d = c - (ll)((b*x+c)/a)*a; ll s = (ll)((b*x+c)/a)*(n+1)*n/2 + n*(ll)((b*x+d)*n/a); return s - f(b*b*r-d*d, a*b, -a*d, (ll)((b*x+d)*n/a)); } int main() { int T;scanf("%d", &T); while(T--) { scanf("%lld%lld", &n, &r); x = sqrt(r); if(x==(int)(x+0.5)) printf("%lld\n", (r&1)? ((n&1)? -1 : 0) : n); else printf("%lld\n", n+4*f(2,1,0,n)-2*f(1,1,0,n)); } return 0; }
参考链接:
1. https://blog.csdn.net/code92007/article/details/97396823
2. https://blog.csdn.net/lych_cys/article/details/51345089
3. https://www.cnblogs.com/xiao-ju-ruo-xjr/p/7157945.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号