SG函数的理解集应用
SG函数
作用
对于一个状态i为先手必胜态当且仅当SG(i)!=0。
转移
那怎么得到SG函数尼。
SG(i)=mex(SG(j))(状态i可以通过一步转移到j)
首先说一下mex。一个集合的mex是最小的没有出现在这个集合里的非负整数。
其实想一下这个也是挺明显的。状态i是先手必败态当前仅当i转移到的状态都是先手必胜态。同样,只要当前状态可以转移到一个先手必败态,那么当前就是先手必胜态。
小定理
对于两个独立的游戏A,B,他们的SG函数=SG(A) ^ SG(B)(其实这个也是有SG函数的定义保证的)
这个比较难描述,看一下后面的题就明白了。
Nim游戏
level 1
有N堆石子。A B两个人轮流拿,A先拿。每次只能从一堆中取若干个,可将一堆全取走,但不可不取,拿到最后1颗石子的人获胜。假设A B都非常聪明,拿石子的过程中不会出现失误。给出N及每堆石子的数量,问最后谁能赢得比赛。
分析:
这就是上面那个小定理的应用了。考虑只有一堆石子的情况,肯定是先手必胜态。
SG函数肯定是石子个数(由SG的定义,显然)。
那么整个游戏的SG函数就是每个子游戏(只有一堆石子的情况)SG函数的异或之和。
所以这个题只要判断所有石子个数异或和是不是0即可。
level 2
有一堆共n个石子,Alice和Bob轮流从这堆石子里面取1到k个,不能取者输。问是否存在先手必胜策略
分析:
状态i可以转移到的状态就是i-j(1<=j<=k)
所以SG(i)=mex(SG(i-j)) (1<=j<=k)
假设k=3
则SG(0)=0,SG(1)=1,SG(2)=2,SG(3)=3,SG(4)=0,SG(5)=1...
可见,当 i%k==1时,SG(i)=0.
仔细想一下就能发现为啥了。这就相当于拿个长度为k的窗口在这个序列里面滑动。新进来的数的SG函数就是刚好从窗口的出去的那个。即先手拿x颗时,后手拿 (k+1-x) 颗。
level 3
有一堆n个石子,Alice和Bob轮流这堆石子里面取石子,每次可以取l-r个,问是否存在先手必胜态。
分析:
介绍一个通法:找规律!!
假设l=3,r=7
SG=[0,0,0,1,1,1,2,2,2,3,0,0.....]
即前 l 个为0,接着 l+r 个非0。
当然可以写个程序找

#include<bits/stdc++.h> using namespace std; const int maxn = 100 + 10; int sg[maxn], n; int L, R; void init_sg() { for(int i = 0;i < L;i++) sg[i] = 0; for(int i = L;i <= n;i++) { set<int>s; for(int j = L;j <= R;j++) if(i >= j) s.insert(sg[i-j]); int t = 0; while(s.count(t)) t++; sg[i] = t; } } int main() { L = 3, R = 7; n = 100; init_sg(); for(int i = 0;i < n;i++) { printf("%d ", sg[i]); if(i % (L+R) == (L+R-1)) printf("\n"); } }
可写成SG(i)=i%(l + r) / l,但是要怎么证明呢?
一般可以用数学归纳法证明!
level 4
有n堆石子,第i堆石子有a[i]个,Alice和Bob轮流操作,每次可以从一堆石子里面取任意多个,也可以把一堆石子分成两堆。不能操作者输。问是否存在先手必胜态。
分析
继续找规律!
SG(i)=mex(SG(i - j),SG(i-j) ^ SG(j))
SG(i-j)是从石子里面取j个,SG(i-j)^SG(j)是将石子分成j和i-j两堆。
level 5
有1堆石子,Alice和Bob轮流操作,每次可以从一堆里面取当前个数的因数个(不能是本身),不能操作者(剩下一个)输。问是否存在先手必胜态。
分析:
SG(i) = mex(SG(i-k)) (k|i)
打表如下:
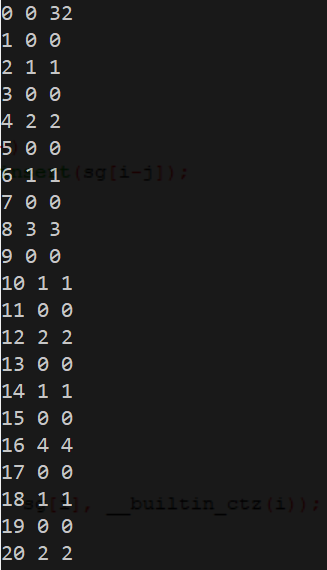
找规律可以发现
SG(i) = __builtin_ctz(i)
也就是i的末尾0的个数
level 6
有1堆石子,Alice和Bob轮流操作,每次可以从一堆里面取与当前个数互质的数字个石子,不能操作者输,问是否存在先手必胜态
分析:
SG(i)=mex(SG(i-j)) (gcd(i,j)=1)
打表如下:
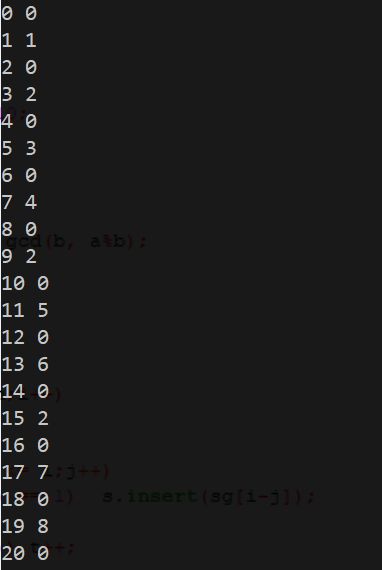
发现,对于偶数,SG为0.
对于奇数,SG为最小质因子的编号(就是最小质因子是第几个质数)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号