用1 x 2的多米诺骨牌填满M x N矩形的方案数（完美覆盖）

题意

用 $1 \times 2$ 的多米诺骨牌填满 $M \times N$ 的矩形有多少种方案，$M \leq 5,N < 2^{31}$，输出答案模 $p$.

分析

当 $M=3$时，假设前 $n-2$列已经填满，$n-1$ 列不全，现要向左推进一列。

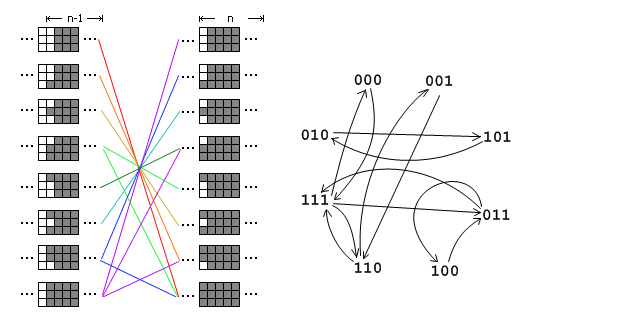
 每列只有8种情况，如果一种情况能转移到另一种则连一条边。

答案就是从“111”出发恰好走 $n$ 步又回到“111” 的路径数，这个问题等价于求转移矩阵的 $n$ 次方.

确定转移矩阵，使用矩阵快速幂，$mat[7][7]$ 就是答案。

实现

$M=3$ 时，

#include<cstdio>
#include<cstring>
using namespace std;

typedef long long ll;
struct matrix
{
    int r, c;
    ll mat[8][8];
    matrix(){
        memset(mat, 0, sizeof(mat));
    }
};
const ll p = 1e9+7;
int n, m=3;

matrix mul(matrix A, matrix B)   //矩阵相乘
{
    matrix ret;
    ret.r = A.r; ret.c = B.c;
    for(int i = 0;i < A.r;i++)
        for(int k = 0;k < A.c;k++)
            for(int j = 0;j < B.c;j++)
            {
                ret.mat[i][j] = (ret.mat[i][j] + A.mat[i][k] * B.mat[k][j])%p;
            }
    return ret;
}

matrix mpow(matrix A, int n)
{
    matrix ret;
    ret.r = A.r; ret.c = A.c;
    for(int i = 0;i < ret.r;i++)  ret.mat[i][i] = 1;
    while(n)
    {
        if(n & 1)  ret = mul(ret, A);
        A = mul(A, A);
        n >>= 1;
    }
    return ret;
}

int  main()
{
    scanf("%d", &n);
    matrix A;
    A.r = A.c = 8;
    A.mat[0][7] = A.mat[1][6] = A.mat[2][5] = A.mat[3][4] = A.mat[3][7] =
    A.mat[4][3] = A.mat[5][2] = A.mat[6][1] = A.mat[6][7] = A.mat[7][0] = A.mat[7][3] = A.mat[7][6] = 1;
    A = mpow(A, n);
    printf("%lld\n", A.mat[7][7]);
}

 

 

参考链接：

1. http://www.matrix67.com/blog/archives/276

2. https://blog.csdn.net/starcuan/article/details/19076095

3. https://blog.csdn.net/heyuchang666/article/details/68067962