杨氏矩阵的基本操作
杨氏矩阵既可以用来当堆,又可以当成平衡树。。在具体存储的时候,我们将没有元素的地方置为无穷大∞。
增
假如现在我们有这样一个矩阵,要向其中插入一个元素7。
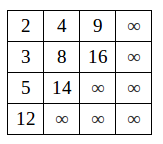
只要这个矩阵不是满的,初始时应该将待插入的元素放到矩阵的右下角。
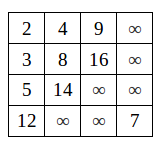
现在我们要将它移动到矩阵中合适的位置。如果它的上边和左边都有元素,那么就选择其中最大的一个与它交换;如果并不是上边和左边都有值,那么选择先向上移动或者先向左移动都可以。考虑到矩阵存储的特性,先向上可能会更好一些。这里我们选择优先向上调整。7往上走发现为空,一直走到矩阵的左上角。这时候上面没有值了,跟左边比较,发现9>7,所以7跟9交换;再跟4比较,7>4,所以停止。
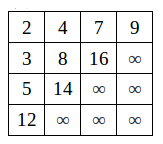
删
删除元素时:
①将要删除的位置置为∞;
②将该∞元素向下、向右调整,选择其中最小的一个数,与之交换位置。
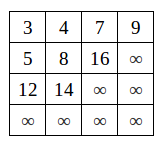
假如现在要删除m[0][0]的元素:
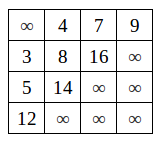
它分别跟3、5、12交换后,杨氏矩阵变成下面这个样子:
这种调整元素使矩阵满足杨氏矩阵性质的过程就做yangify(是不是想起了堆里面的heapify,哈哈)。
查
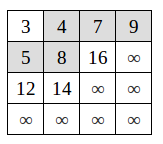
整个矩阵,最小的元素在左上角,最大的元素在右下角。而对于左下角和右上角,它们都满足一个方向的元素大于自己、另一个方向的元素小于自己(很像平衡二叉树啊)。利用这个特性,查找可以从左下角或是右上角开始,鉴于之前插入时我们选择优先右上角,这里查找我们也优先查找右上角。
假设我们要查找值为5的元素。从右上角开始,9、7都比5要大,所以往左;4比5小,往下移动;8比5大,往左;找到5了,停止。
改
修改的话就是先用上面的方法找到元素,然后yangify就可以了。
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号