2018ccpc吉林 E:THE TOWER——数形结合
题目
给你一个圆锥(位于坐标原点,告诉你高h 和底面半径 r),和一个点(x,y,z)并告诉你这个点的速度,
让你求点和圆锥相撞的最小时间(保证一定相撞)
分析
易知,将直线的参数方程与圆锥曲面的方程联立,但是可能产生增根,具体情形如下:
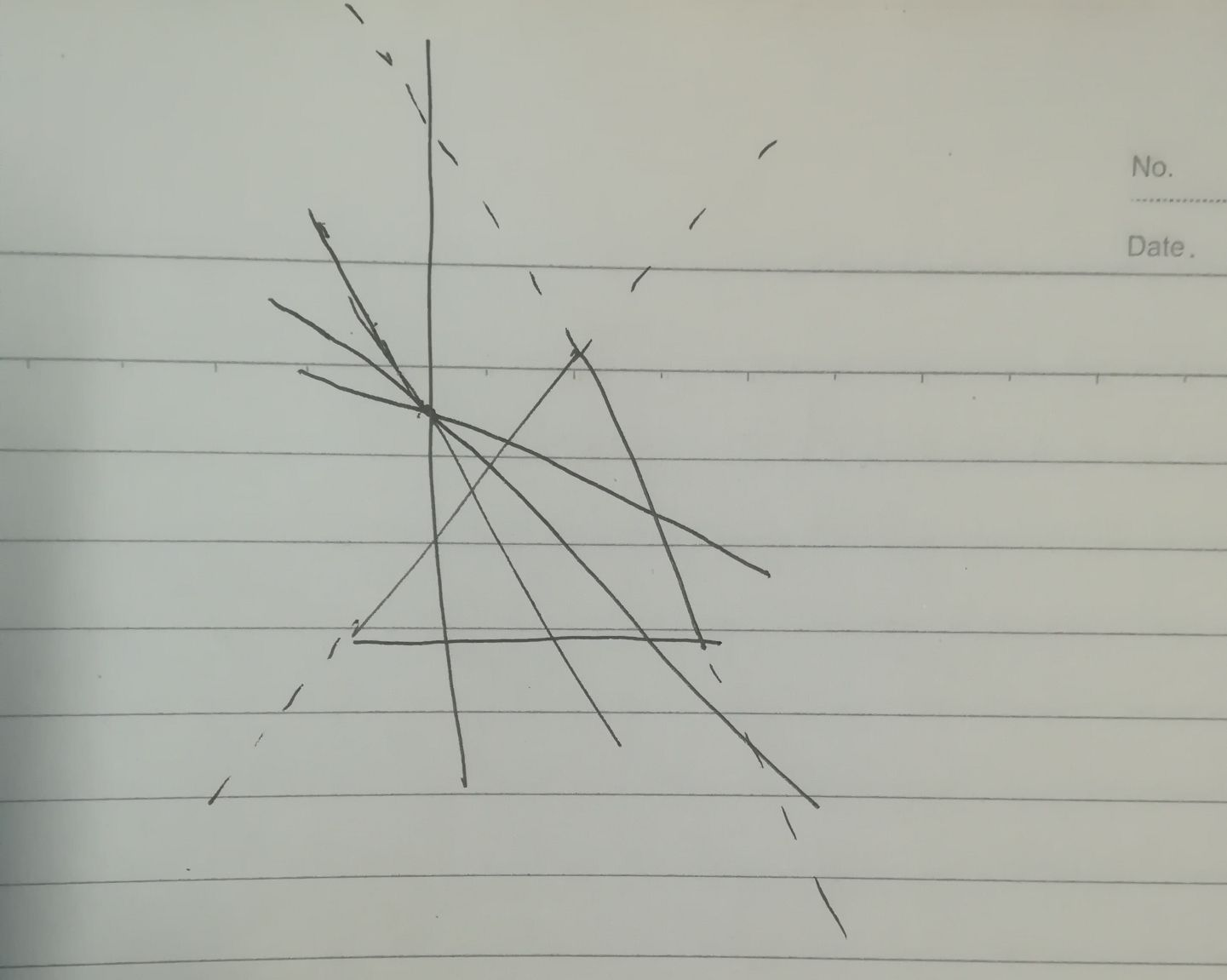
其实我们不必区分具体情况,只需交点在曲面上的时间的最小值。
注意两点,一是判断交点在曲面上不能使用x,y约束,而应该使用z,试考虑如下情况:
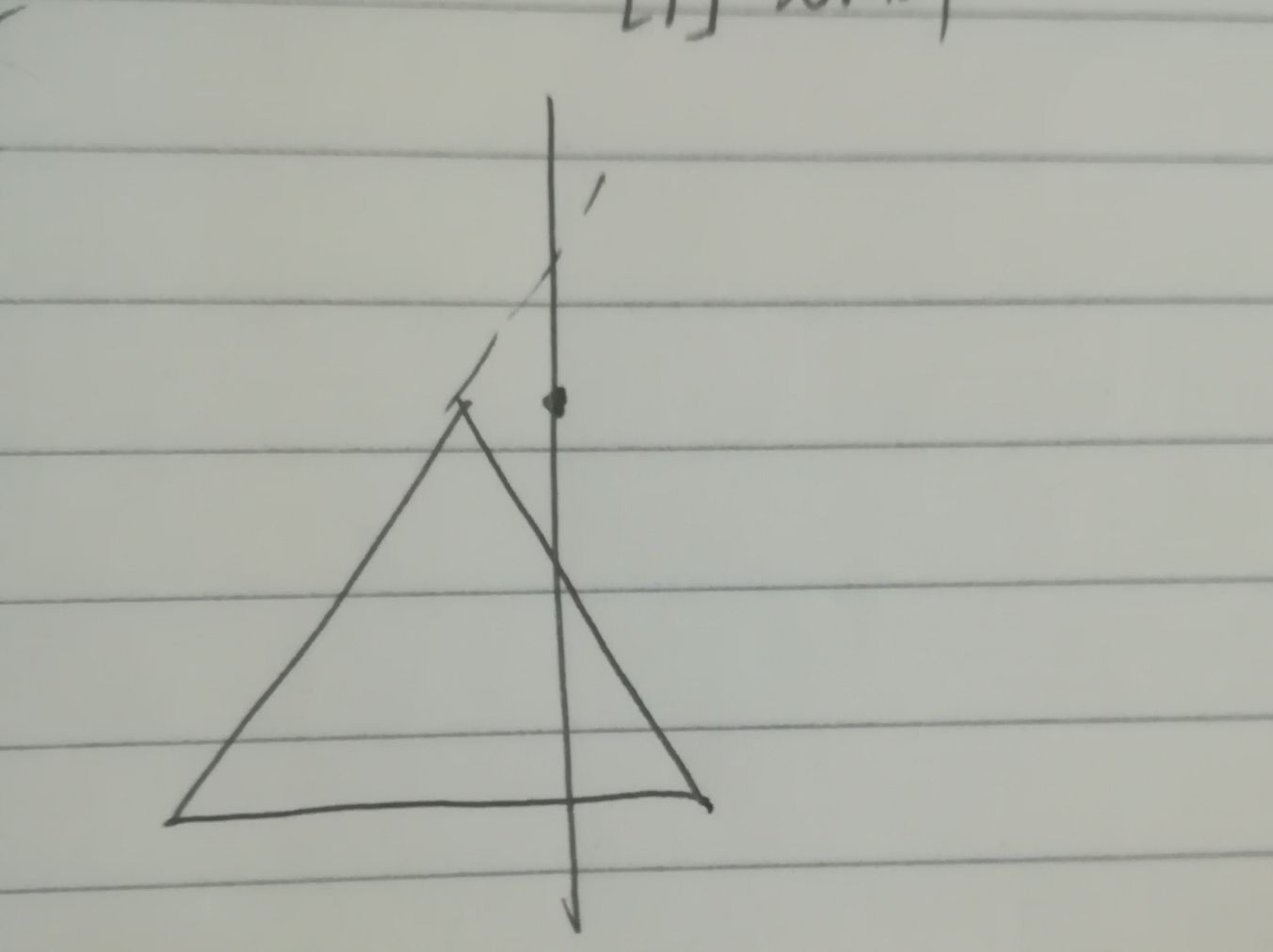
二是可能与底面相交,也不用特判,只需与前面的时间取较小值。
#include<bits/stdc++.h> using namespace std; double r, h, x, y, z, vx, vy, vz; int main() { int T, kase = 0; scanf("%d", &T); while(T--) { scanf("%lf%lf", &r, &h); scanf("%lf%lf%lf", &x, &y, &z); scanf("%lf%lf%lf", &vx, &vy, &vz); double a = h*h*vx*vx + h*h*vy*vy - r*r*vz*vz; double b = 2*h*h*x*vx + 2*h*h*y*vy - 2*r*r*z*vz + 2*r*r*h*vz; double c = h*h*x*x + h*h*y*y - h*h*r*r - r*r*z*z + 2*r*r*h*z; double detal = sqrt(b * b - 4 * a *c); double t1 = (-b + detal) / (2 * a); //double x1 = x + vx * t1; double z1 = z + vz * t1; double t2 = (-b - detal) / (2 * a); //double x2 = x + vx * t2; double z2 = z + vz * t2; //printf("a:%lf b:%lf c:%lf\n", a, b, c); //printf("detal:%lf t1:%lf t2:%lf\n", detal, t1, t2); //printf("Case %d: ", ++kase); double ans = 1e18; if(z1 >= 0 && z1 <= h && t1 > 0) ans = min(ans, t1); //²»ÄÜÓÃx,zÀ´ÅÐ¶Ï if(z2 >= 0 && z2 <= h && t2 > 0) ans = min(ans, t2); double tmpt = -z / vz; double tmpx = x + vx * tmpt; double tmpy = y + vy *tmpt; if(fabs(vz)>1e-6){ if(tmpx >= -r && tmpx <= r && tmpy >= -r && tmpy <= r && tmpt > 0) ans = min(ans, tmpt); } printf("Case %d: %.10lf\n", ++kase, ans); } return 0; }
参考链接:https://blog.csdn.net/du_mingm/article/details/89791220
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号