区间第K小——可持久化线段树模板
概念
可持久化线段树又叫主席树,之所以叫主席树是因为这东西是fotile主席创建出来的。
可持久化数据结构思想,就是保留整个操作的历史,即,对一个线段树进行操作之后,保留访问操作前的线段树的能力。
最简单的方法,每操作一次,建立一颗新树。这样对空间的需求会很大。而注意到,对于点修改,每次操作最多影响 $O(\log n)$ ![]() 个节点,于是,其实操作前后的两个线段树,结构一样,因此可以共享未被影响的节点,被影响的就新建节点。于是,这样的线段树,每次操作需要O(log2(n))的空间。
个节点,于是,其实操作前后的两个线段树,结构一样,因此可以共享未被影响的节点,被影响的就新建节点。于是,这样的线段树,每次操作需要O(log2(n))的空间。
线段树对于每个n的分解是唯一的,所以n相同的线段树结构相同,这也是实现可持久化线段树的基础。
分析
对于区间第K小,
先用
sort + unique 进行离散化操作;然后以离散化后的元素作为底层(接下来大概就是用线段树按顺序记录每个数字出现的次数)。关键来了:以不同的区间建立不同的版本,及1..1为1号,1..2为2号,1..7为7号,以此类推。 查询区间
l..r 需要查询两个版本:ver[l-1]与ver[r],同步查询两棵树,并对查询到的内容相减便是l..r中该范围内的数据(以数字出现字数为关键词)。相当于线段树的前缀和。#include<bits/stdc++.h> using namespace std; const int maxn = 2e5 + 100; int n, m, size_disc; //size_disc是离散化之后的长度 int n_init[maxn], n_disc[maxn]; //原数组 离散化后的数组 int rt[maxn], lc[maxn << 5], rc[maxn << 5], sum[maxn << 5]; //rt:不同版本的根节点 lc/rc: 左儿子、右儿子(公用) sum: 和(公用) int node_cnt, pnt_disc; //node总计数, pnt_disc: A中数字对应B中的值 void build(int& last_node, int l, int r) { last_node = ++ node_cnt; sum[last_node] = 0; if(l == r) return; int mid = (l + r) >> 1; build(lc[last_node], l, mid); build(rc[last_node], mid+1, r); } int modify(int pre_rt, int l, int r) { int new_rt = ++node_cnt; lc[new_rt] = lc[pre_rt]; rc[new_rt] = rc[pre_rt]; sum[new_rt] = sum[pre_rt] + 1; int mid = (l + r) >> 1; if(l == r) return new_rt; if(mid >= pnt_disc) lc[new_rt] = modify(lc[new_rt], l, mid); else rc[new_rt] = modify(rc[new_rt], mid+1, r); return new_rt; } int query(int rt1, int rt2, int k, int l, int r) { //printf("rt1:%d rt2:%d k:%d l:%d r:%d ", rt1, rt2, k, l, r); if(l == r) return l; int mid = (l + r) >> 1; int tmp = sum[lc[rt2]] - sum[lc[rt1]]; //int tmp=sum[lc[rt2]]-sum[lc[rt1]]; //printf("tmp:%d k:%d\n", tmp, k); int ans; if(tmp >= k) ans = query(lc[rt1], lc[rt2], k, l, mid); else ans = query(rc[rt1], rc[rt2], k-tmp, mid+1, r); return ans; } void print_debug() { printf("node_cnt: %d\n", node_cnt); for(int i = 0;i <= node_cnt;i++) printf("%d lc:%d rc:%d sum:%d\n", i, lc[i], rc[i], sum[i]); } int main() { scanf("%d%d", &n, &m); for(int i = 1;i <= n;i++) { scanf("%d", &n_init[i]); n_disc[i] = n_init[i]; } sort(n_disc+1, n_disc+n+1); //先排序再进行离散化 size_disc = unique(n_disc+1, n_disc+n+1) - (n_disc+1); node_cnt = 0; build(rt[0], 1, size_disc); for(int i = 1;i <= n;i++) { pnt_disc = lower_bound(n_disc+1, n_disc+size_disc+1, n_init[i]) - n_disc; //改了1 rt[i] = modify(rt[i-1], 1, size_disc); //只在上一个版本的基础上修改 } for(int i = 0;i <m;i++) { int l, r, k; scanf("%d%d%d", &l, &r, &k);l--; int ans = query(rt[l], rt[r], k, 1, size_disc); printf("%d\n", n_disc[ans]); } }
其中,遍历1~n建立n棵线段树的过程如下:
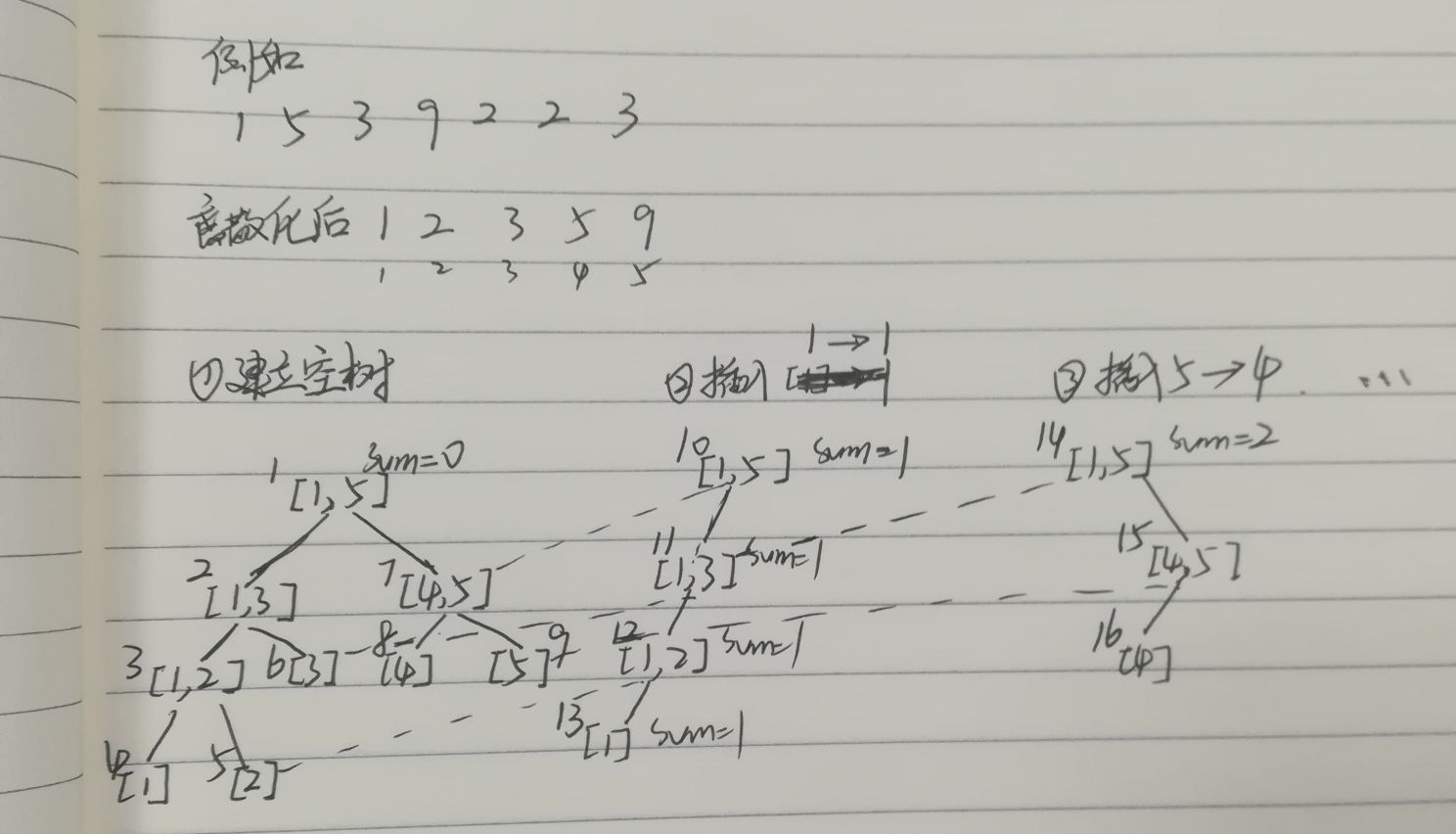
其中第i棵是建立在i-1棵的基础上,加上它们的n相同,结构也完全相同,两颗线段树相减就是这两个操作之间的变化值。
参考链接:
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号