卷积及其应用

卷积的定义

向量的计算

给定向量：$a=(a_0,a_1,.,a_{n-1}), \ b = (b_0,b_1,...,b_{n-1})$

向量和：$a+b = (a_0+b_0, a_1+b_1, ... ,a_{n-1}+b_{n-})$

内积：$a\cdot b = a_0b_0 + a_1b_1 +...+a_{n-1}b_{n-1}$

卷积：$a*b = (c_0, c_1,...,c_{2n-2})$，其中$C_k = \sum_{i+j=k,\ i,j< n} a_ib_j, \ k = 0,1,...,2n-2$

即$$ \begin{aligned}
C_0 &= a_0b_0 \\ C_1 &= a_0b_1+a_1b_0 \\C_2 &= a_0b_2 + a_1b_1 + a_2b_0 \\ \cdots
\end{aligned} $$

这就是卷积的基本公式，即将下标和相同的数相乘再相加，对于这个公式我们有矩阵形式的解释。

卷积的含义

构造如下形式的矩阵：

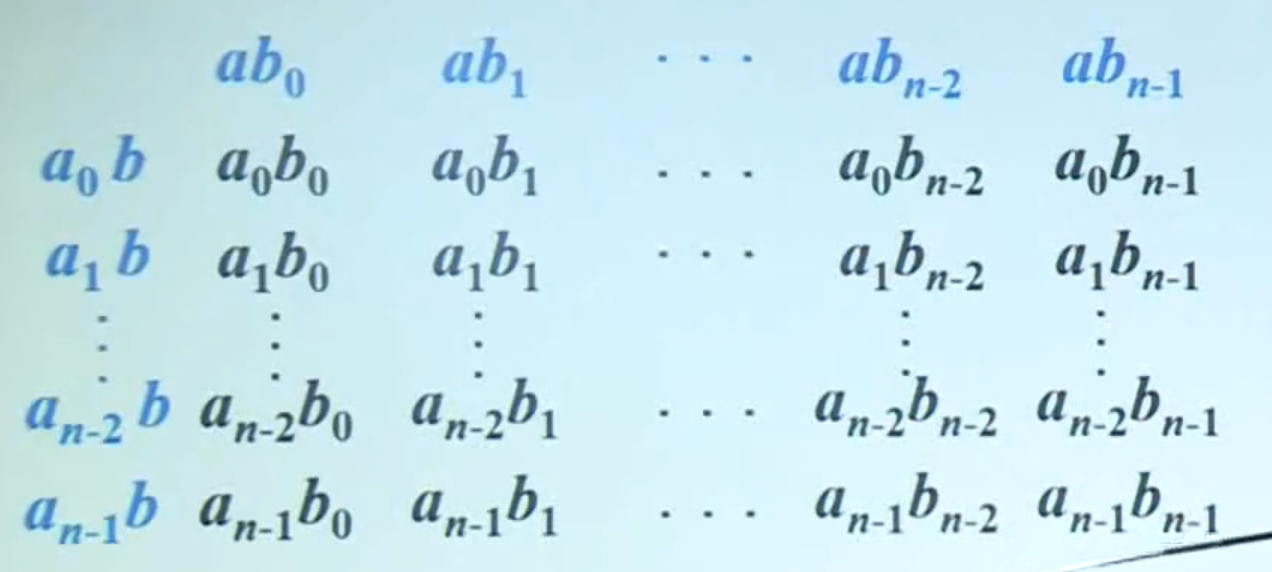
可发现，每条斜线的项之和恰好是卷积中的各个分量。

例如，$C_{n-1}$

计算实例

向量$a=(1,2,4,3)$和向量$b=(4,2,8,0)$进行运算。

例如卷积结果中的28，既可以通过前3项交叉相乘$1\times 8 + 2 \times 2 + 4 \times 4$得到，也可以矩阵形式斜线相加得到。

卷积与多项式乘法的关系

多项式乘法：$C(x) = A(x)B(x)$

$A(x) = a_0 + a_1x + a_2x^2+...+a_{m-1}x^{m-1}$

$B(x) = b_0 + b_1x + b_2x^2 + ... + b_{n-1}x^{n-1}$

$C(X) = a_0b_0 + (a_0b_1 + a_1b_0)x+(a_0b_2 + a_1b_1 + a_2b_0)x^2 + ...+ a_{m-1}b_{n-1}x^{m+n-2}$，其中$x^k$的系数

$$c_k = \sum _{i+j=k \\  i\in\{0,1,...,m-1\} \\  j\in\{0,1,...,n-1\} } a_ib_j, \ k=0,1,...,m+n-2$$

 可见，多项式乘法的系数就是卷积的结果。

卷积应用：信号平滑处理

    由于噪声干扰，对信号需要平滑处理。

 

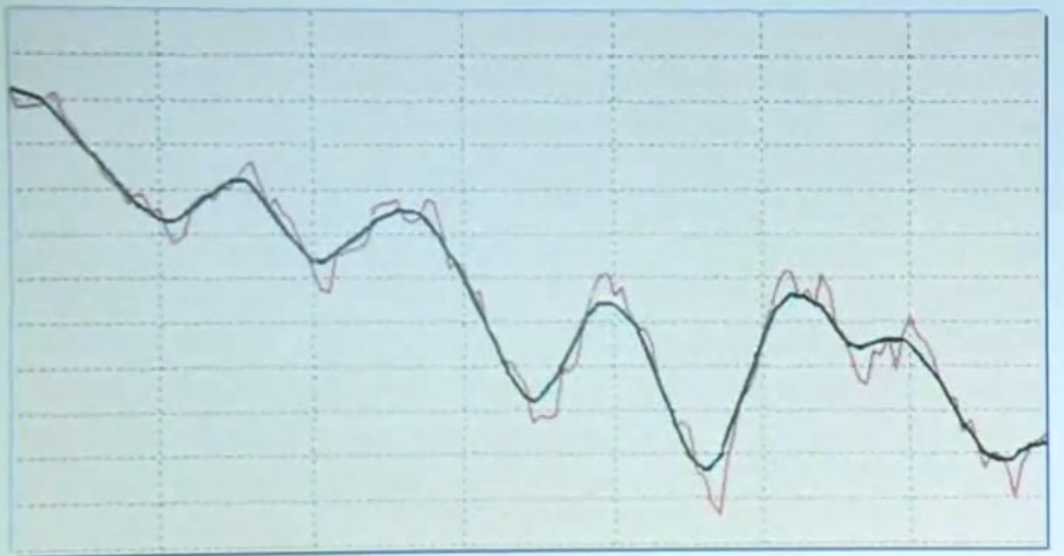
    如图，红色的线是有噪音的情况，黑色的线就是处理以后的结果，它把噪音去掉了，这种处理叫平滑处理。

平滑处理

信号向量：$a = (a_0,a_1,...,a_{m-1})$

$b = (b_{2k}, b_{2k-1}, ..., b_0) = (w_{-k}, ..., w_k)$

于是${a_i}' = \sum _{s=-k} ^k a_{i+s}b_{k-s} = \sum _{s=-k}^k = a_{i+s}w_s$

 

     由于a是升序，b是降序，所以对应项的下标和相等，相乘再相加也即是一个卷积值，用新的值代替原来位置的值。把b向量看作一个2k+1长度窗口在a上移动，少数项有误差。

实例

 

 矩阵表示如下：