Aho-Corasick自动机
在模式匹配问题中,如果模板有很多个,KMP算法就不太适合了。因为每次查找一个模板。都要遍历整个文本串。可不可以只遍历一次文本串呢?可以,方法是把所有模板组成一个大的状态转移图(称为$Aho-Corasick$自动机,简称$AC$自动机),而不是每个模板各建一个状态转移图。注意到KMP的状态转移图是线性的字符串加上失配边组成的,不难想到AC自动机是Trie加上失配边组成的。
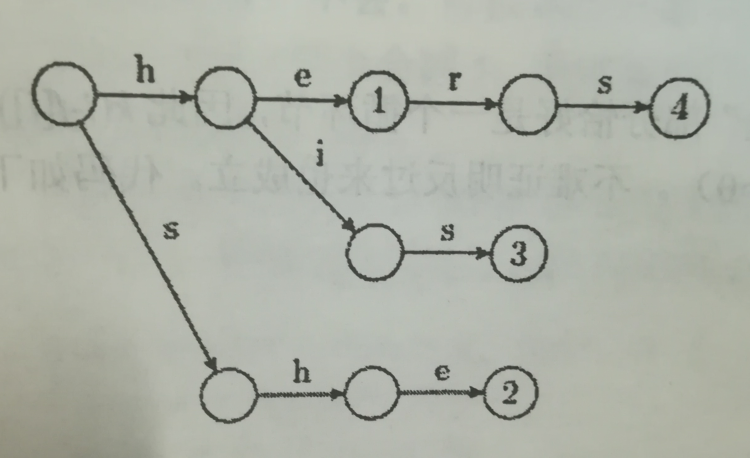
下图是$\{he,she,his,hers \}$的Trie。
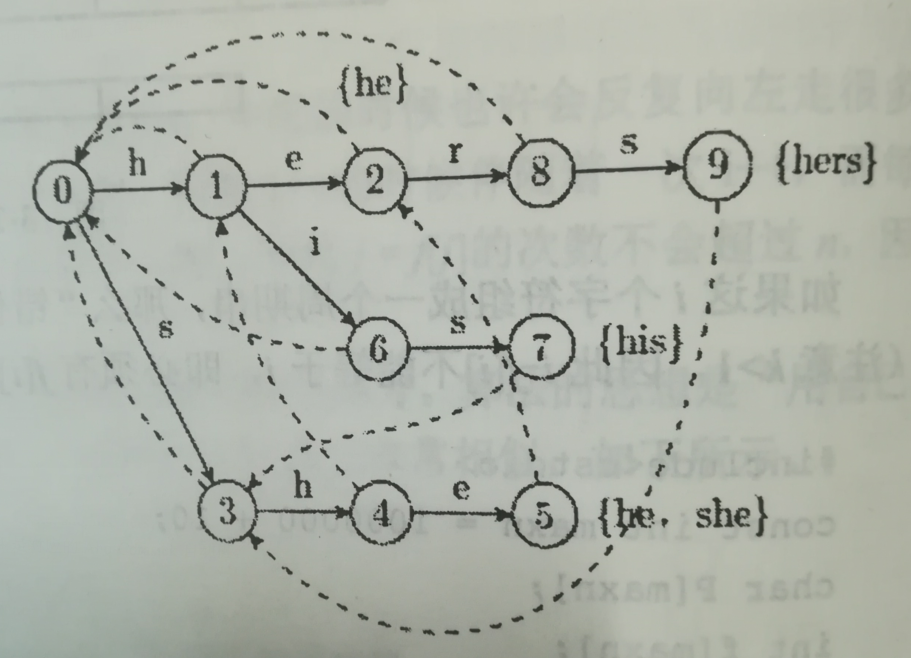
下图是对应的Aho-Corasick自动机。
如果已经构造好AC自动机,匹配算法几乎和KMP是一样的,代码如下:
//在T中找模板 void find(const char* T) { int n = strlen(T); int j = 0; //当前结点编号,初始为根节点 for (int i = 0; i < n; i++) //文本串当前指针 { int c = idx(T[i]); while (j && !ch[j][c]) j = f[j]; //顺着失配边走,直到可以匹配 j = ch[j][c]; if (val[j]) print(j); else if (last[j]) print(last[j]); //找到了 } }
其中print函数为:
//递归打印以结点j结尾的所有字符串 void print(int j) { if (j) { printf("%d: %d\n",j, val[j]); print(last[j]); } }
代码中出现了一个陌生的数组last,下面解释以下。和Trie一样,我们认为所有val[j]>0的结点都是单词结点,反之亦然。但和Trie不同的是,同一个结点可能对应多个字符串的结尾,如图所示:
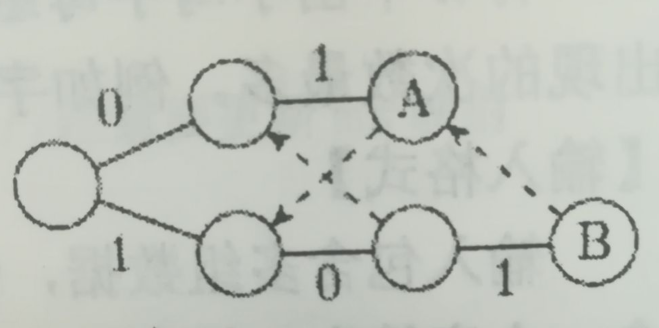
结点B不仅意味着找到串101,还意味着找到串01。换句话说,当找到一个模板后,应该顺着失配指针往回走,,看看有没有其它串。当然,失配指针不一定指向一个单词结点(比如,两个串是101和010,那么上图的结点A不是单词结点),为了提高效率,这里增设一个指针last[j],表示结点j沿着失配指针往回走时,遇到的下一个单词结点编号。这个last[j]在正规文献中叫后缀链接(suffix link)。
计算失配函数的方式和KMP很接近,只是把线性递归改成了按照BFS顺序递推,代码如下:
//计算fail函数 void getFail() { queue<int>q; f[0] = 0; //初始化队列 for (int c = 0; c < sigma_size; c++) { int u = ch[0][c]; if (u) { f[u] = 0; q.push(u); last[u] = 0; } } //按BFS序计算fail while (!q.empty()) { int r = q.front(); q.pop(); for (int c = 0; c < sigma_size; c++) { int u = ch[r][c]; if (!u) continue; q.push(u); int v = f[r]; while (v && !ch[v][c]) v = f[v]; f[u] = ch[v][c]; last[u] = (val[f[u]] ? f[u] : last[f[u]]); } } }
由于失配工程比较复杂,要反复沿着失配边走,在实践中常常会把上述AC自动机改造一下,把所有不存在的边补上,即把计算失配函数中的语句"if(!u) continue;"改成:if(!u){ ch[r][c] = ch[f[r]][c]; continue;}
这样,就完全不需要失配函数了,而是对所有的转移一视同仁也就是说,find函数中的语句"while(j && !ch[j][c]) j=f[j];"; 可以直接完全删除。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号