树状数组入门讲解
平常我们会遇到一些对数组进行维护查询的操作,比较常见的,修改某点的值、求某个区间的和。
即给定一个n个元素的数组$A_1、A_2、..., A_n$,你的任务是设计一个数据结构,支持以下两种操作:
- $Add(x,d)$操作:让$A_x$增加$d$。
- $Query(L,R)$:计算$A_L+A_{L+1}+...+A_R$。
如果按简单的前缀和处理,修改操作是$O(1)$,区间查询操作是$O(n)$,当操作次数为m时,最坏的时间复杂度是$O(mn)$,$n$很大时显然无法接受。如何让$Query$和$Add$都能快速完成呢?有一种称为二叉搜索树($Binary Indexed Tree, BIT$)的数据结构(俗称树状数组),可以很好地解决这个问题。为此,我们需要先介绍$lowbit$。
lowbit
对于正整数$x$,我们定义$lowbit(x)$为$x$的二进制表达式中最右边的1所对应的值(而不是这个比特的序号)。比如,38288的二进制是1001010110010000,所以$lowbit(38288)=16$(二进制是10000)。在程序实现中,$lowbit(x)=x\&-x$。为什么呢?回忆一下,计算机里的整数采用补码表示,因此$-x$实际上是$x$按位取反末尾加一的结果,如图所示:
 两者按位取与之后,前面的部分全部变0,之后lowbit保持不变。
两者按位取与之后,前面的部分全部变0,之后lowbit保持不变。
原理
如下图所示是一颗典型的BIT,由15个结点组成,编号为1~15.
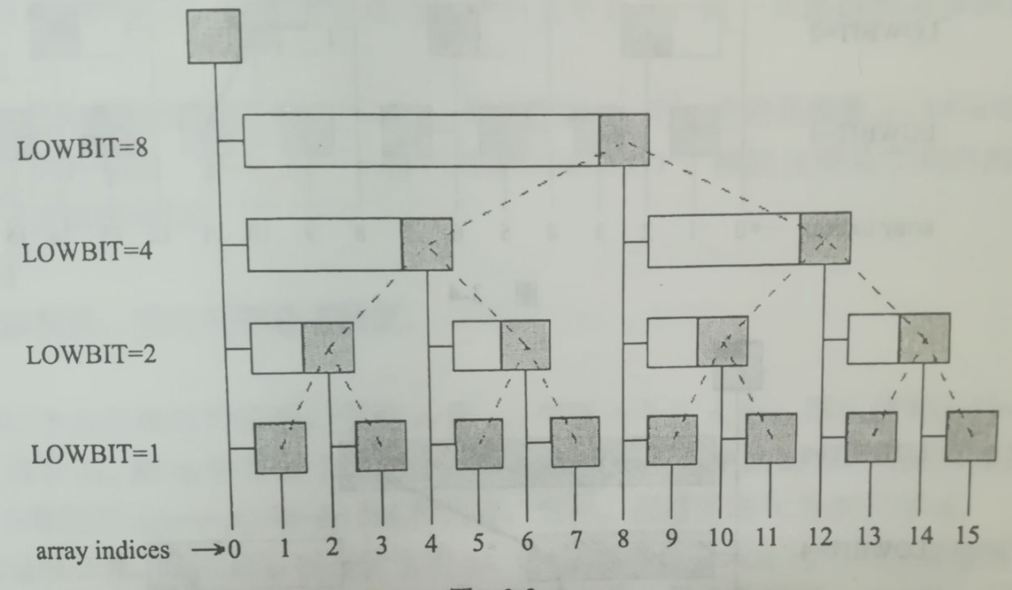
灰色结点是BIT中的结点(白色长条的含义稍后叙述),每一层结点的lowbit相同,而且lowbit越大越靠近根。图中的虚线是BIT中的边(在代码中并不需要存储这些边,这里画出来只是为了更好的理解BIT)。注意编号为0的点是虚拟结点,它并不是树的一部分,但是它的存在可以让算法理解起来更容易一些。
对于结点$i$,如果它是左子结点,那么它的父节点编号就是$i+lowbit(i)$;如果它是右子结点,那么它的父节点的编号是$i-lowbit(i)$(请自行验证)。搞清楚树的结构之后,构造一个辅助数组C,其中$C_i=A_{i-lowbit(i)+1}+A_{i-lowbit(i)+2}+...+A_i$
换句话说,C中的每个元素都是A数组中的一段连续和。到底是哪一段呢?BIT中,每个灰色结点$i$都属于一个以它自身结尾的水平长条(对于lowbit=1的那些点,“长条”就是那个结点自身),这个长条中的数之和就是$C_i$。比如结点12的长条就是从9~12,即$C_2=A_9+A_{10}+A_{11}+A_{12}$。同理,$C_6=A_5+A_6$。这个等式及其重要,请花一些时间来验证"$C_i$就是以$i$结尾的水平长条内的元素之和"这一事实。
有了$C$数组之后,如何计算前缀和$S_i$呢?顺着结点$i$往左走,边走边往上爬(注意并不一定沿着树中的边往爬),把沿途经过的$C_i$累加起来就可以了(请自行验证,沿途经过的$C_i$所对应的长条不重复不遗漏地包含了所有需要累加地元素),如图所示
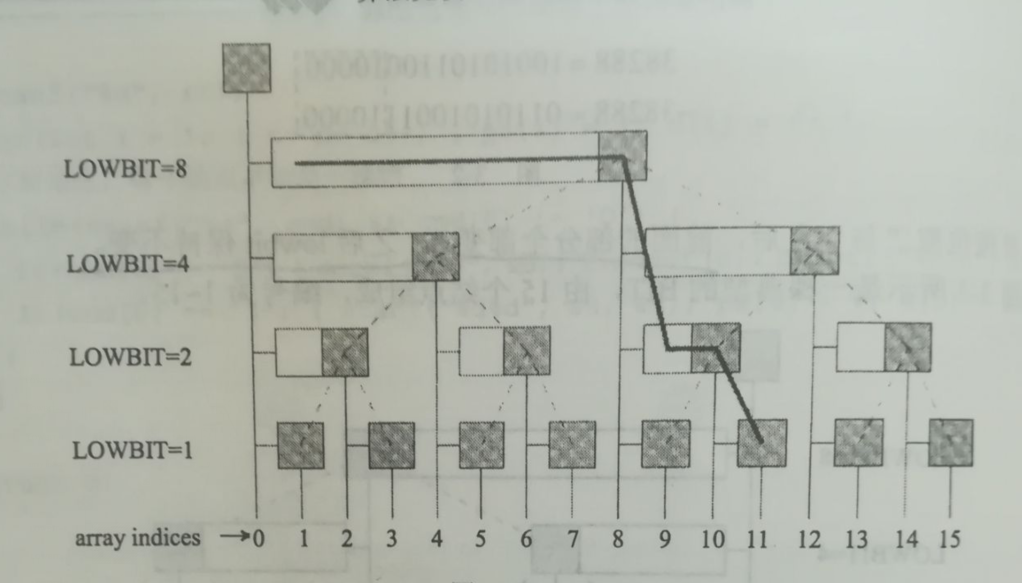
而如果修改了一个$A_i$,需要更新$C$数组中哪些元素呢?顺着结点$C_i$开始往右走,边走边“往上爬”(同样不一定沿着树中的边爬),沿途修改所有结点对应的$C_i$即可(请自己验证,有且仅有这些结点对应的长条包含被修改的元素),如图所示:
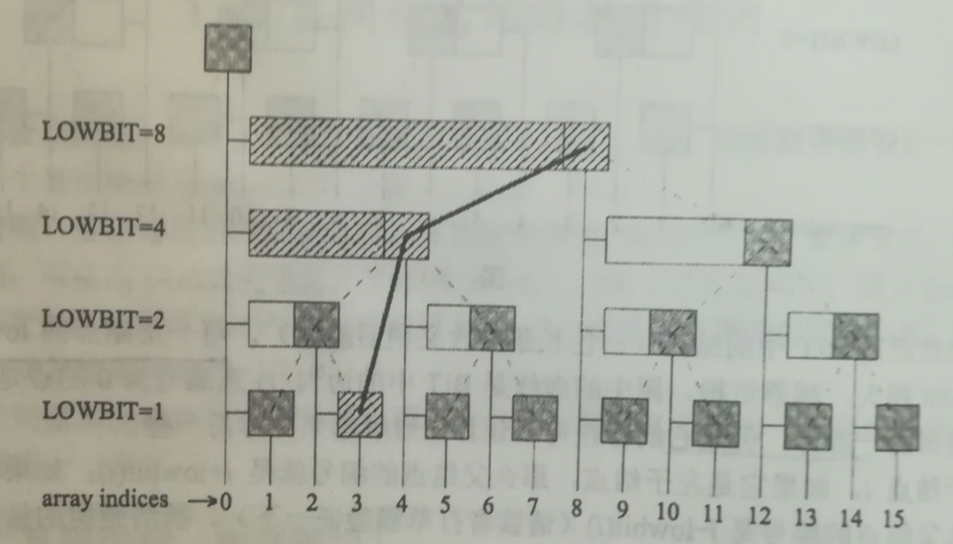 不难证明。两个操作的时间复杂度均为O(logn)。预处理的方法是先把$A$数组和$C$数组清空,然后执行$n$次$add$操作,总时间复杂度为$O(nlogn)$。
不难证明。两个操作的时间复杂度均为O(logn)。预处理的方法是先把$A$数组和$C$数组清空,然后执行$n$次$add$操作,总时间复杂度为$O(nlogn)$。
代码
两个操作的代码如下:
int sum(int x) //前缀和 { int ret = 0; while (x > 0) { ret += C[x]; x -= lowbit(x); } return ret; } void add(int x, int d) { while (x <= n) { C[x] += d; x += lowbit(x); } }
完整代码:

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 6 const int maxn = 10000 + 10; 7 int a[maxn],C[maxn],n; 8 9 int lowbit(int x) 10 { 11 return x & -x; 12 } 13 int sum(int x) 14 { 15 int ret = 0; 16 while (x > 0) 17 { 18 ret += C[x]; 19 x -= lowbit(x); 20 } 21 return ret; 22 } 23 void add(int x, int d) 24 { 25 while (x <= n) 26 { 27 C[x] += d; 28 x += lowbit(x); 29 } 30 } 31 void init() 32 { 33 memset(C, 0, sizeof(C)); 34 for (int i = 1; i <= n; i++) 35 add(i, a[i]); 36 } 37 38 int main() 39 { 40 scanf("%d", &n); 41 for (int i = 1; i <= n; i++) scanf("%d", &a[i]); 42 init(); 43 printf("%d\n", sum(10)); 44 printf("%d\n", sum(5)); 45 add(5, 3); 46 printf("%d", sum(5)); 47 48 return 0; 49 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号