MINST手写数字识别(二)—— 卷积神经网络(CNN)
今天我们的主角是keras,其简洁性和易用性简直出乎David 9我的预期。大家都知道keras是在TensorFlow上又包装了一层,向简洁易用的深度学习又迈出了坚实的一步。
所以,今天就来带大家写keras中的Hello World , 做一个手写数字识别的cnn。回顾cnn架构:
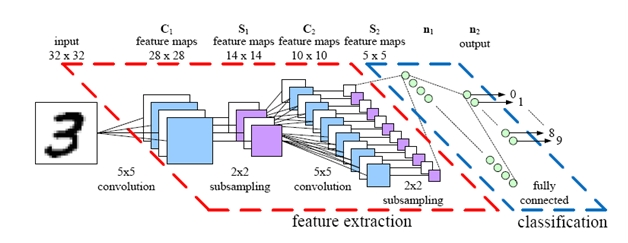
我们要处理的是这样的灰度像素图:
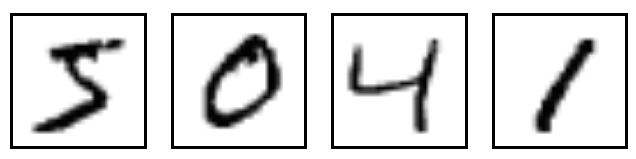
我们先来看跑完的结果(在Google Colab上运行):
x_train shape: (60000, 28, 28, 1) 60000 train samples 10000 test samples Train on 60000 samples, validate on 10000 samples Epoch 1/12 60000/60000 [==============================] - 12s 193us/step - loss: 0.2672 - acc: 0.9166 - val_loss: 0.0648 - val_acc: 0.9792 Epoch 2/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0892 - acc: 0.9731 - val_loss: 0.0433 - val_acc: 0.9866 Epoch 3/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0666 - acc: 0.9796 - val_loss: 0.0353 - val_acc: 0.9874 Epoch 4/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0578 - acc: 0.9829 - val_loss: 0.0327 - val_acc: 0.9887 Epoch 5/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0483 - acc: 0.9856 - val_loss: 0.0295 - val_acc: 0.9901 Epoch 6/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0433 - acc: 0.9869 - val_loss: 0.0313 - val_acc: 0.9895 Epoch 7/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0379 - acc: 0.9879 - val_loss: 0.0267 - val_acc: 0.9913 Epoch 8/12 60000/60000 [==============================] - 9s 147us/step - loss: 0.0353 - acc: 0.9891 - val_loss: 0.0263 - val_acc: 0.9913 Epoch 9/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0327 - acc: 0.9904 - val_loss: 0.0275 - val_acc: 0.9905 Epoch 10/12 60000/60000 [==============================] - 9s 146us/step - loss: 0.0323 - acc: 0.9898 - val_loss: 0.0260 - val_acc: 0.9914 Epoch 11/12 60000/60000 [==============================] - 9s 147us/step - loss: 0.0286 - acc: 0.9913 - val_loss: 0.0283 - val_acc: 0.9909 Epoch 12/12 60000/60000 [==============================] - 9s 147us/step - loss: 0.0267 - acc: 0.9922 - val_loss: 0.0268 - val_acc: 0.9906 Test loss: 0.026836299882206368 Test accuracy: 0.9906
所以我们跑的是keras_mnist_cnn.py。最后达到99%的预测准确率。首先来解释一下输出:
测试样本格式是28*28像素的1通道,灰度图,数量为60000个样本。
测试集是10000个样本。
一次epoch是一次完整迭代(所有样本都训练过),这里我们用了12次迭代,最后一次迭代就可以收敛到99.06%预测准确率了。
接下来我们看代码:
from __future__ import print_function import keras from keras.datasets import mnist from keras.models import Sequential from keras.layers import Dense, Dropout, Flatten from keras.layers import Conv2D, MaxPooling2D from keras import backend as K
一开始我们导入一些基本库,包括:
- minst数据集
- Sequential类,可以封装各种神经网络层,包括Dense全连接层,Dropout层,Cov2D卷积层,等等
- 我们都直到Keras支持两个后端TensorFlow和Theano,可以在
$HOME/.keras/keras.json中配置
接下来,我们准备训练集和测试集,以及一些重要参数:
# batch_size 太小会导致训练慢,过拟合等问题,太大会导致欠拟合。所以要适当选择 batch_size = 128 # 0-9手写数字一个有10个类别 num_classes = 10 # 12次完整迭代,差不多够了 epochs = 12 # 输入的图片是28*28像素的灰度图 img_rows, img_cols = 28, 28 # 训练集,测试集收集非常方便 (x_train, y_train), (x_test, y_test) = mnist.load_data() # keras输入数据有两种格式,一种是通道数放在前面,一种是通道数放在后面, # 其实就是格式差别而已 if K.image_data_format() == 'channels_first': x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols) x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols) input_shape = (1, img_rows, img_cols) else: x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1) x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1) input_shape = (img_rows, img_cols, 1) # 把数据变成float32更精确 x_train = x_train.astype('float32') x_test = x_test.astype('float32') x_train /= 255 x_test /= 255 print('x_train shape:', x_train.shape) print(x_train.shape[0], 'train samples') print(x_test.shape[0], 'test samples') # 把类别0-9变成独热码 y_train = keras.utils.np_utils.to_categorical(y_train, num_classes) y_test = keras.utils.np_utils.to_categorical(y_test, num_classes)
然后,是令人兴奋而且简洁得令人吃鲸的训练构造cnn和训练过程:
# 牛逼的Sequential类可以让我们灵活地插入不同的神经网络层 model = Sequential() # 加上一个2D卷积层, 32个输出(也就是卷积通道),激活函数选用relu, # 卷积核的窗口选用3*3像素窗口 model.add(Conv2D(32, activation='relu', input_shape=input_shape, nb_row=3, nb_col=3)) # 64个通道的卷积层 model.add(Conv2D(64, activation='relu', nb_row=3, nb_col=3)) # 池化层是2*2像素的 model.add(MaxPooling2D(pool_size=(2, 2))) # 对于池化层的输出,采用0.35概率的Dropout model.add(Dropout(0.35)) # 展平所有像素,比如[28*28] -> [784] model.add(Flatten()) # 对所有像素使用全连接层,输出为128,激活函数选用relu model.add(Dense(128, activation='relu')) # 对输入采用0.5概率的Dropout model.add(Dropout(0.5)) # 对刚才Dropout的输出采用softmax激活函数,得到最后结果0-9 model.add(Dense(num_classes, activation='softmax')) # 模型我们使用交叉熵损失函数,最优化方法选用Adadelta model.compile(loss=keras.metrics.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy']) # 令人兴奋的训练过程 model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, y_test))
完整地训练完毕之后,可以计算一下预测准确率:
score = model.evaluate(x_test, y_test, verbose=0) print('Test loss:', score[0]) print('Test accuracy:', score[1])
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号