WOJ600——水题

第一次做本校OJ的题，被坑的好惨啊！

题目：600.Minimum  Distance  

题目大意：给定平面上3个点A、B、C，求平面上的任一顶点P，使得|PA|+2|PB|+3|PC|。

由于刚好在这之前做了一道模拟退火的“类似”题，打了一遍模拟退火，样例都过不了；

然后又“觉得”可以三分套三分，能过样例，但还是wa了，说好的简单题呢(⁄ ⁄•⁄ω⁄•⁄ ⁄)

后来，发现前两者系数和等于第三者，所以P为C点，就是最小值。证明如下：

 

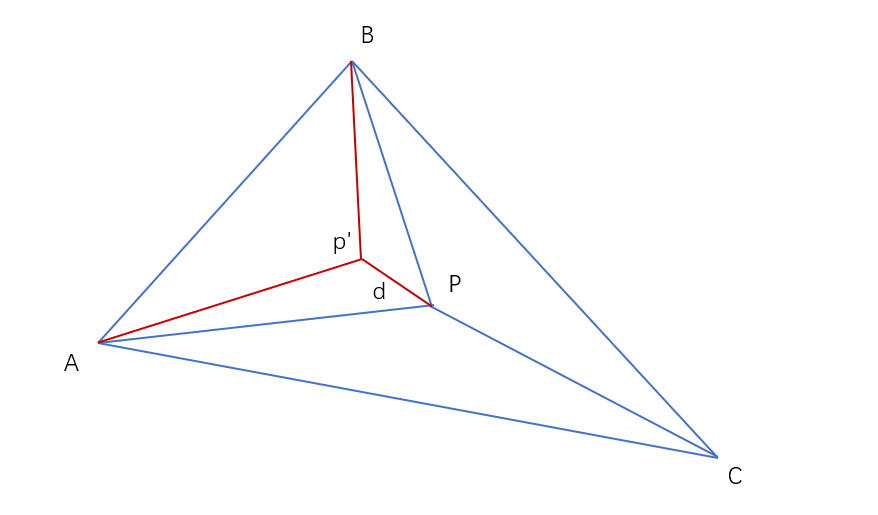
考虑从P移到P’式子值的变化：

令$|{P}'A|-|PA| = {d}' \ \&\&\  |{P}'B| - |PB|={d}'' \ \&\&\  |{P}'C| - |PC| = d$

$\because d >  {d}' \ \&\&\  d >  {d}'' \\$

所以有，

$$\begin{aligned}
\Delta &=|{P}'A|+2|{P}'B|+3|{P}'C|-(|PA|+2|PB|+3|PC|) \\
&=(|{P}'A|-|PA|) + 2(|{P}'B| - |PB|) + 3(|{P}'C| - |PC|)\\
&=-{d}' - 2{d}'' + 3d\\
&=(d-{d}') + 2(d-{d}'')\\
&> 0 \end{aligned}$$

所以，$d$越小越好，即P与C越紧越好，即令P与C重合。

代码实现就很简单了

#include<cstdio>
#include<cmath>
#include<algorithm>
#define long double double
using namespace std;

const int INF = 0x3f3f3f3f;

struct Point
{
    int x, y;
};
Point points[3];

double dist(Point a,Point b)
{
    return sqrt((a.x - b.x) * (a.x - b.x) * 1.0 + (a.y - b.y) * (a.y - b.y) * 1.0);
}

int main()
{
    while (scanf("%d%d%d%d%d%d", &points[0].x, &points[0].y, &points[1].x, &points[1].y, &points[2].x, &points[2].y) == 6)
    {
        double ans = dist(points[0], points[2]) + 2 * dist(points[1], points[2]);
        printf("%.6lf\n", ans);
    }
    return 0;
}