KMP中next数组的理解与应用

 理解

1、next数组一直往前走

next数组一直往前走，得到的所有前缀也是当前主串的后缀，当然了，也是当前主串的前缀。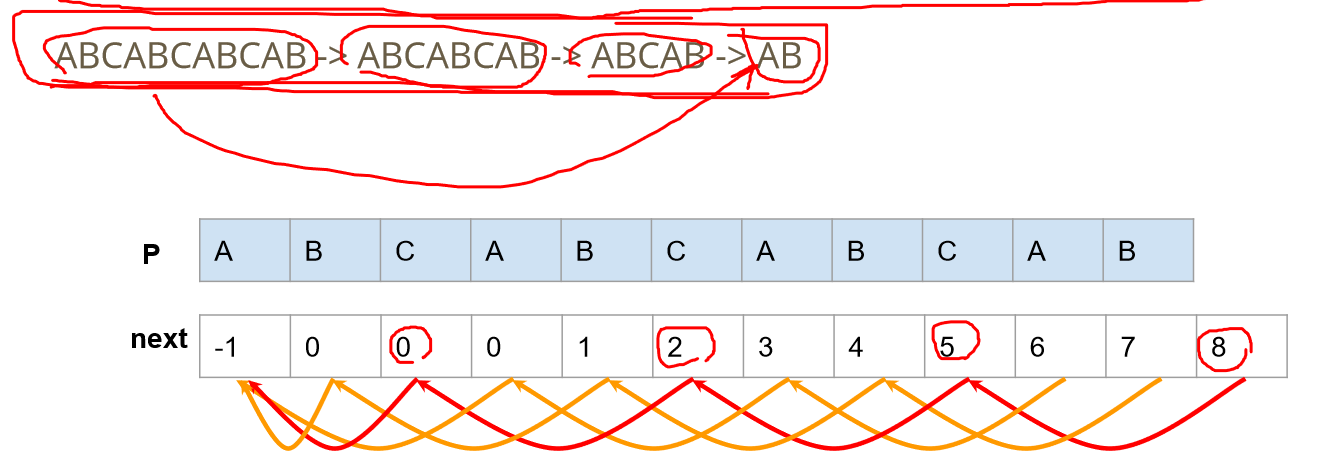

2、周期性字符串

1、周期性字符串$\Leftrightarrow n \,\% \, (n-next[n]) == 0 \ \&\& \ next[n] {\ } {\!}!{=} \  0 $，循环节长度是$n-next[n]$。

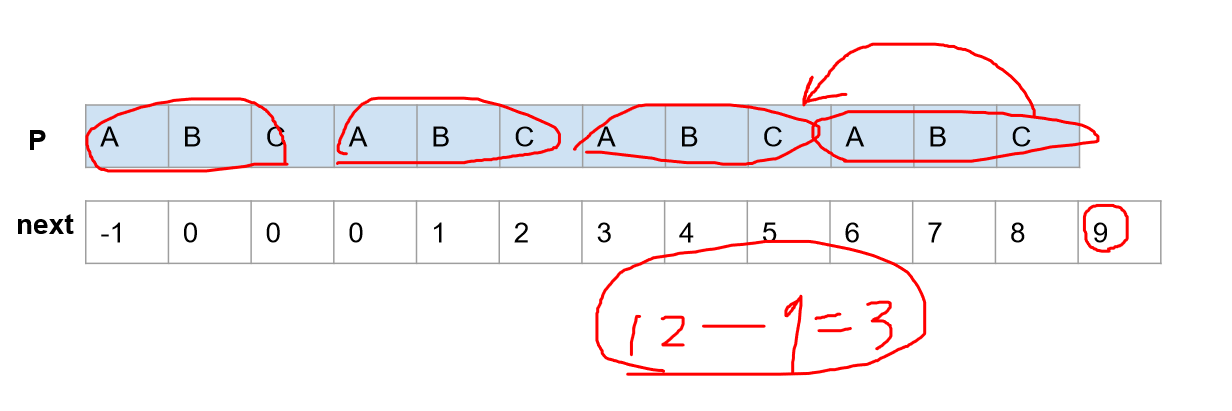
2、next数组往前跳的步长是一样的，除了最后一次。即$i-next[i]$保持恒定。

应用

思路：先求出next数组，然后遍历一遍next数组得到所有字符结尾的字符串循环节的长度及个数

代码：

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 using namespace std;
 5 
 6 const int maxn = 1000000 + 10;
 7 int nexts[maxn],n;
 8 char s[maxn];
 9 
10 void pre_kmp()
11 {
12     int i = 0, j = nexts[0] = -1;
13     while (i < n)
14     {
15         while (j != -1 && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
16         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
17     }
18 }
19 
20 void slove()
21 {
22     pre_kmp();
23     for(int i = 2; i <= n; i++)
24         if (i % (i - nexts[i]) == 0 && nexts[i] != 0)  printf("%d %d\n", i, i / (i - nexts[i]));
25 }
26 
27 int main()
28 {
29     int T = 0;
30     while (scanf("%d",&n) == 1 && n)
31     {
32         scanf("%s", s);
33         s[n] = '#';
34         if (T)  printf("\n");
35         printf("Test case #%d\n", ++T);
36         slove();
37     }
38     return 0;
39 }
View Code

 

思路：先求next数组，再直接求循环节

代码：

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 using namespace std;
 5 
 6 const int maxn = 1000000 + 10;
 7 int nexts[maxn],n;
 8 char s[maxn];
 9 
10 void pre_kmp()
11 {
12     int i = 0, j = nexts[0] = -1;
13     //int n = strlen(s);
14     while (i < n)
15     {
16         while (j != -1 && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
17         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
18     }
19 }
20 
21 void slove()
22 {
23     pre_kmp();
24     if (n % (n - nexts[n]) != 0)  printf("1\n");
25     else  printf("%d\n", n / (n - nexts[n]));
26 }
27 
28 int main()
29 {
30     int T = 0;
31     while (scanf("%s", s) == 1 && s[0] != '.')
32     {
33         n = strlen(s);
34         s[n] = '#'; 
35         slove();
36     }
37     return 0;
38 }
View Code

思路：求所有前缀出现的次数和，由于next数组回退得到的前缀也是主串的后缀，所以所有next回退的次数加上本身的一次取模就是答案。

代码：

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 using namespace std;
 5 
 6 const int mod = 10007;
 7 const int maxn = 200000 + 10;
 8 int nexts[maxn], n;
 9 char s[maxn];
10 
11 void pre_kmp()
12 {
13     int i = 0, j = nexts[0] = -1;
14     //int n = strlen(s);
15     while (i < n)
16     {
17         while (j != -1 && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
18         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
19     }
20 }
21 
22 void slove()
23 {
24     int ans = n;
25     pre_kmp();
26     for (int i = n; i > 0; i--)
27     {
28         int k = nexts[i];
29         while (k > 0)
30         {
31             ans = (ans + 1) % mod;
32             k = nexts[k];
33         }
34     }
35     printf("%d\n", ans);
36 }
37 
38 int main()
39 {
40     int T;
41     scanf("%d", &T);
42     while (T--)
43     {
44         scanf("%d", &n);
45         scanf("%s", s);
46         slove();
47     }
48     return 0;
49 }
View Code

思路：题目大意：问至少添加多少个字符，使得这个字符串有至少两个循环节。若本身有两个循环节返回0，否则补充至两个循环节。

代码：

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 using namespace std;
 5 
 6 const int mod = 10007;
 7 const int maxn = 200000 + 10;
 8 int nexts[maxn], n;
 9 char s[maxn];
10 
11 void pre_kmp()
12 {
13     int i = 0, j = nexts[0] = -1;
14     n = strlen(s);
15     while (i < n)
16     {
17         while (j != -1 && s[i] != s[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等
18         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1
19     }
20 }
21 
22 void slove()
23 {
24     pre_kmp();
25     int len = n - nexts[n];
26     if (n % len  == 0 && nexts[n] != 0)  printf("0\n");
27     else  printf("%d\n", len - nexts[n] % len);
28 }
29 
30 int main()
31 {
32     int T;
33     scanf("%d", &T);
34     while (T--)
35     {
36         scanf("%s", s);
37         slove();
38     }
39     return 0;
40 }
View Code

 

 

参考链接：

1、https://vjudge.net/contest/278481#overview

2、https://blog.csdn.net/hkh746392783/article/details/52015293

posted @ 2019-01-31 12:36  Rogn  阅读(2800)  评论(0)  编辑  收藏  举报